

That is another of your odd notions,said the Prefect, who had the fashion of calling everything
oddthat was beyond his comprehension, and thus lived amid an absolute legion of
oddities.
The Purloined Letter
A polyform oddity is a geometric figure with binary symmetry or better, formed by joining an odd number of congruent polyforms. Oddities are also known as Sillke figures, after Torsten Sillke, who first studied them systematically.
This page shows minimal known oddities and similar constructions for various polyforms with various symmetries.
[Polyominoes and Polykings] [Polyiamonds and Polymings] [Polyhexes, Polyhings, and Polybrexes] [Polypents] [Polyhepts] [Polyocts] [Polyenns] [Polydecs] [Polyhendecs] [Polydodecs] [Polyaboloes/Polytans] [Polycairos] [Polykites] [Polygems] [Polygolds] [Polykagomes] [Polybirds] [Polycubes] [Polyquoins]
 | Trihex Oddities. Trihex oddities with specific symmetries. |
 | Tetrahex Oddities. Tetrahex oddities with specific symmetries. |
 | Pentahex Oddities. Oddities for pentahexes, with specific symmetries. |
 | Pentahex Pair Oddities with Full Symmetry. Full-symmetry polyhexes tiled with an odd number of two different pentahexes. |
 | Pentahex Pair Oddities with Dual Orthogonal Symmetry. Polyhexes with dual orthogonal symmetry tiled with an odd number of two different pentahexes. |
 | One-Sided Pentahex Oddities. Oddities for pentahexes that may not be reflected. |
 | The Magic Pentahex Pair Polyhex Oddity. The same odd polyhex is tiled with 153 different pairs of pentahexes. |
 | Tetrahex-Pentahex Oddities. Full-symmetry polyhexes tiled with an odd number of copies of a tetrahex and a pentahex. |
 | Trihex-Pentahex Oddities. Full-symmetry polyhexes tiled with an odd number of copies of a trihex and a pentahex. |
 | Hexahex Oddities. Hexahex oddities with specific symmetries. |
 | Heptahex Oddities. Oddities for polyhexes with 7 cells, with specific symmetries. |
 | Polyhex Tri-Oddities. Tri-oddities for polyhexes of order up to 5. |
 | Pentahex Pair Tri-Oddities. Tri-oddities for pairs of pentahexes. |
 | Pentahex Pair Tri-Oddities with Horizontal Symmetry. Horizontally symmetric tri-oddities for pairs of pentahexes. |
 | Pentahex Pair Tri-Oddities with Vertical Symmetry. Vertically symmetric tri-oddities for pairs of pentahexes. |
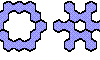 | Hexahex Tri-Oddities. Tri-oddities for hexahexes. |
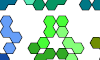 | Polyhing Oddities. Oddities for polyhings. |
 | Tribrex Oddities. Oddities for tribrexes. |
 | Tetrabrex Oddities. Oddities for tetrabrexes. |
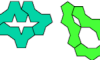 | Tetrapent Oddities. Oddities for tetrapents. |
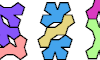 | Tetrapent Pair Oddities. Oddities for pairs of tetrapents. |
 | Tetrapent Triplet Oddities. Oddities for sets of three tetrapents. |
 | Pentapent Oddities. Oddities for pentapents. |
 | Tetrahept Oddities. Oddities for tetrahepts. |

 | Polyoct Oddities. Oddities for polyocts of order 1 through 5. |
 | Pentenn Oddities. Oddities for pentenns. |
 | Polydec Oddities. Oddities for polydecs. |
 | Tetrahendec Oddities. Oddities for tetrahendecs. |
 | Polydodec Oddities. Oddities for polydodecs with 1–4 cells. |
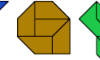 | Polyabolo Oddities. Oddities for polyaboloes. |
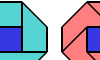 | Diabolo-Triabolo Pair Oddities. Full-symmetry oddities for a diabolo and a triabolo. |
 | Triabolo-Tetrabolo Pair Oddities. Full-symmetry oddities for a triabolo and a tetrabolo. |
 | Diabolo-Pentabolo Pair Oddities. Full-symmetry oddities for a diabolo and a pentabolo. |
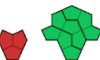 | Polycairo Oddities. Oddities for polycairos. |
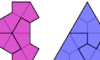 | Polykite Oddities. Oddities for polykites. |
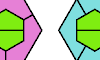 | Trikite-Tetrakite Pair Oddities. Joint oddities for a trikite and a tetrakite. |
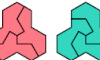 | Polygem Oddities. Oddities for polygems. |
 | Trigem Pair Oddities. Oddities for pairs of trigems. |
 | Tetragold Oddities. Oddities for tetragolds. |
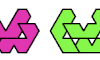 | Polykagome Oddities. Oddities for polykagomes. |
 | Polybird Oddities. Oddities for polybirds. |
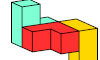 | Minimal Oddities for the L Tricube. Oddities for the L tricube with every even polycube symmetry. |
 | Minimal Oddities for the P Pentacube. Oddities for the P pentacube with every even polycube symmetry. |
 | Pentacube Oddities with Full Symmetry. Full-symmetric oddities for pentacubes. |
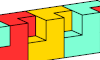 | Pentacube Oddities with Orthogonal Mirror Symmetry. Orthogonal mirror-symmetric oddities for pentacubes. |
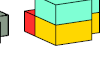 | Pentacube Oddities with Diagonal Mirror Symmetry. Diagonal mirror-symmetric oddities for pentacubes. |
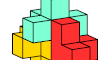 | Pentacube Oddities with Orthogonal Rotary Symmetry. Orthogonal rotationally symmetric oddities for pentacubes. |
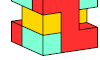 | Pentacube Oddities with Plane Diagonal Rotary Symmetry. Plane diagonal rotationally symmetric oddities for pentacubes. |
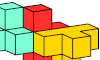 | Pentacube Oddities with Inverse Symmetry. Point-symmetric oddities for pentacubes. |
 | Pentacube Oddities with 4-Rotary Symmetry. Rotary 90° oddities for pentacubes. |
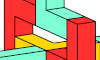 | Pentacube Oddities with Dual Orthogonal Mirror Symmetry. Rectangular-symmetric oddities for pentacubes. |
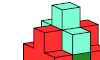 | Pentacube Oddities with Dual Diagonal Mirror Symmetry. Oblique rectangular-symmetric oddities for pentacubes. |
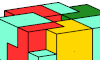 | Pentacube Oddities with Square Symmetry. Square (dual orthogonal + 4-rotary) oddities for pentacubes. |
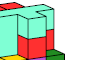 | Pentacube Oddities with Square Box Symmetry. Dicubic (square-box) oddities for pentacubes. |
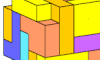 | Pentacube Pair Full Oddities. Full-symmetry oddities formed by copies of two pentacubes. |
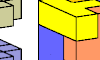 | Tetracube-Pentacube Pair Full Oddities. Full-symmetry oddities formed by copies of a tetracube and a pentacube. |
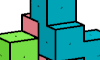 | Triquoin Oddities. Minimal oddities formed by copies of a triquoin. |