An oddity is a figure with binary symmetry formed by an odd number of copies of a polyform. Here are the minimal known oddities for polygems of orders 1–4. The black trigem has no solution; the gray trigems and most of the tetragems are unsolved. Please write if you find a smaller solution or solve an unsolved case.
See also Galvagni Figures for Polygems.

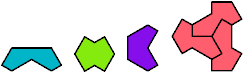



David Smith, Joseph Samuel Myers, Craig S. Kaplan, and Chaim Goodman-Strauss proved in 2023 that the third tetragem in the top row can tile the plane, and cannot tile the plane periodically. Thanks to Ed Pegg for letting me know of this.
Last revised 2023-03-23.