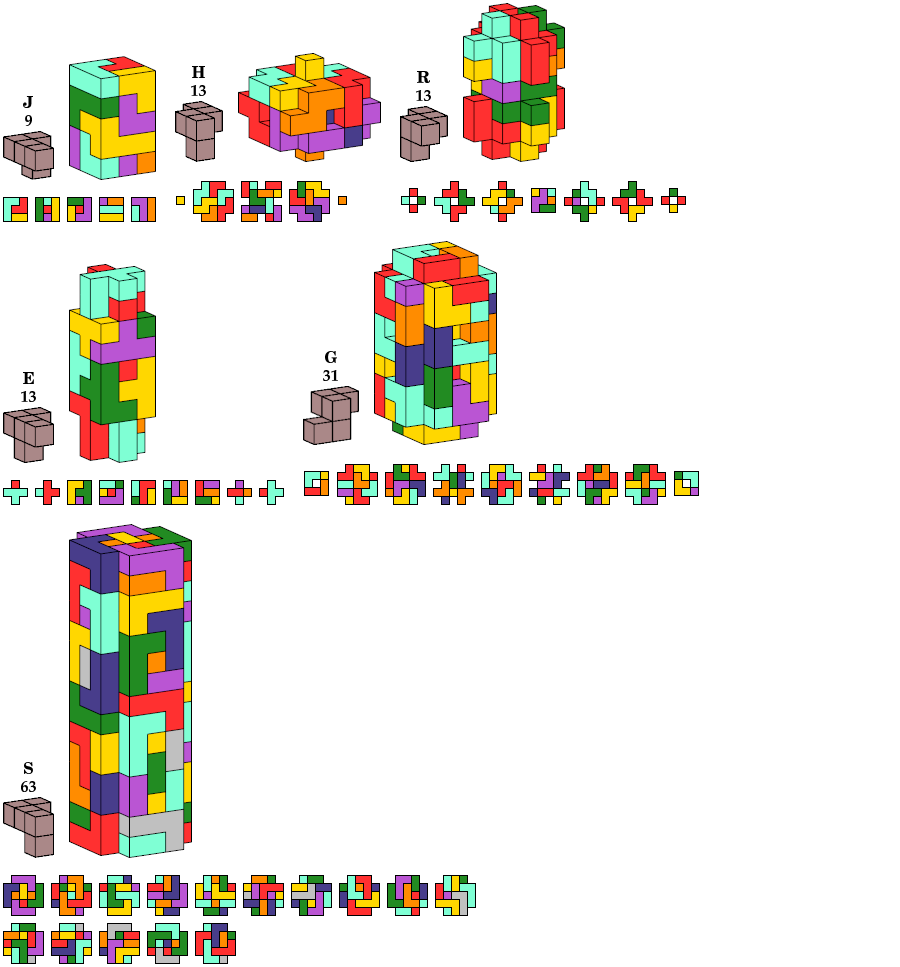Pentacube Oddities with Square Box Symmetry
Introduction
A pentacube is a solid made of five cubes joined
face to face.
An oddity (or Sillke Figure)
is a figure with even symmetry
formed by an odd number of copies of a polyform.
Polycubes have 33 symmetry
classes (including asymmetry),
and 31 of them have even order.
That is too many to show on one page.
Instead I show only pentacube oddities with square box symmetry.
In all pictures, the cross-sections are shown from top to bottom.
If you find a smaller solution, please write.
For other classes of symmetry, see:
Square Box Symmetry
Square box symmetry is 90° rotary symmetry about one orthogonal axis
with mirror symmetry in all three orthogonal directions.
The smallest example of a polycube with square box
symmetry and no stronger symmetry
is the dicube:

Achiral Pentacubes
The solutions for pentacubes
I and
X
are trivial.
Those pentacubes already have square box symmetry.
The solutions for pentacubes
A,
K,
M,
N, and
V
are their smallest known oddities with full (achiral cubic/octahedral)
symmetry.
No smaller solutions are known.
The solution for pentacube T
is formed by joining two prime boxes.
No smaller solution is known.
The solution for pentacubes
F,
W,
and
Z
are minimal solutions for the
corresponding pentominoes.
No smaller solutions are known.
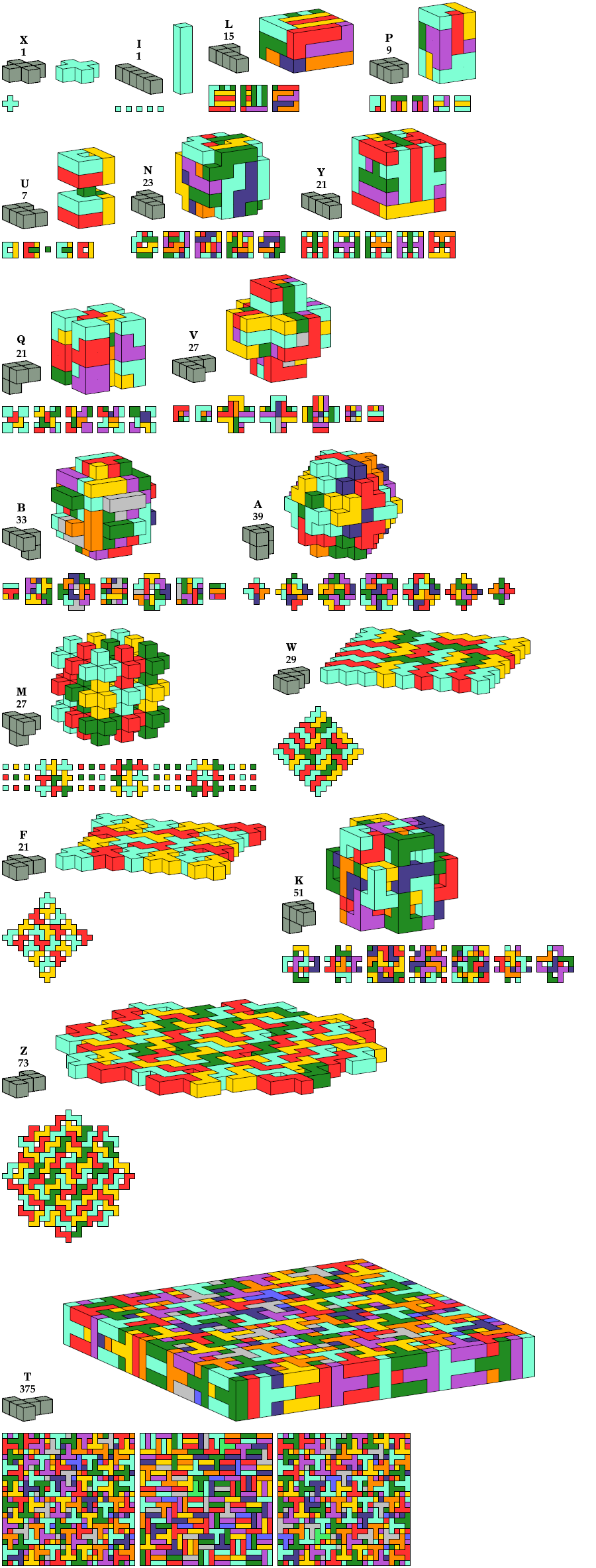
Chiral, Disallowing Reflection
The solution for the S pentacube
is formed by joining three copies of the minimal known odd box.
No smaller solution is known.
The solutions for the E
and H pentacubes have full (achiral cubic/octahedral)
symmetry. No smaller solutions are known.
No solution is known for the G pentacube.
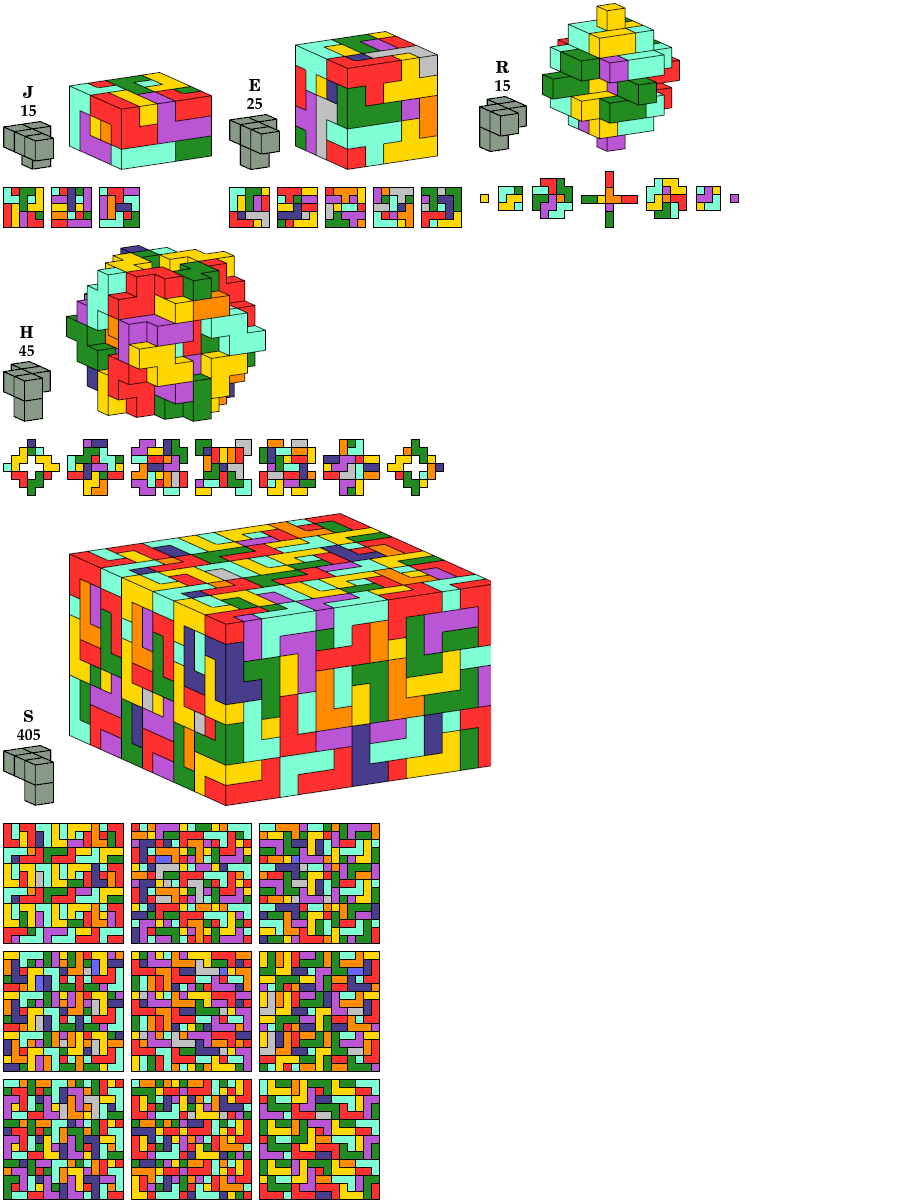
Chiral, Allowing Reflection
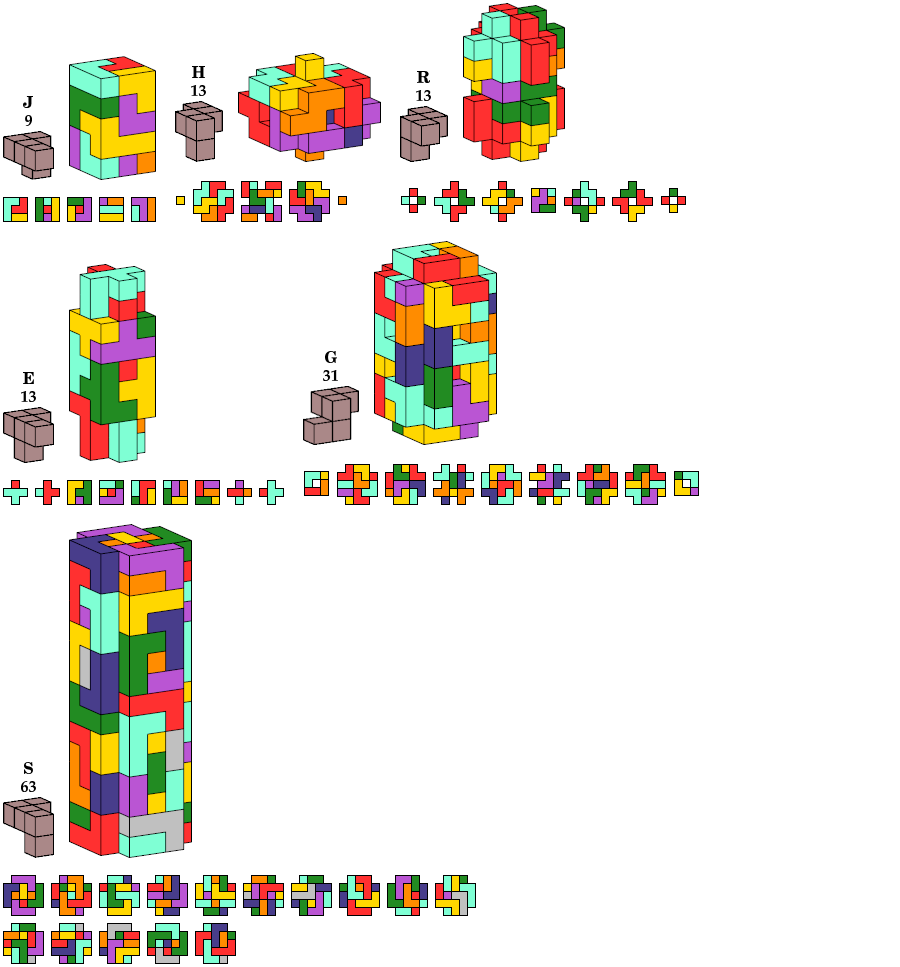
Last revised 2024-04-20.
Back to Polyform Oddities
<
Polyform Curiosities
Col. George Sicherman
[ HOME
| MAIL
]