Pentacube Oddities with 4-Rotary Symmetry
Introduction
A pentacube is a solid made of five cubes joined
face to face.
An oddity (or Sillke Figure)
is a figure with even symmetry
formed by an odd number of copies of a polyform.
In 1996, Torsten Sillke reported
having found a point-symmetric arrangement of 17 F pentacubes.
He asked whether 17 is the least such odd number,
and more generally whether an odd number of copies of a polycube can be arranged
to achieve any given symmetry.
This was the earliest known mention of polyform oddities.
Polycubes have 33 symmetry classes (including asymmetry),
and 31 of them have even order.
That is too many to show here.
Instead I show only oddities with 90° rotary symmetry around
an orthogonal axis.
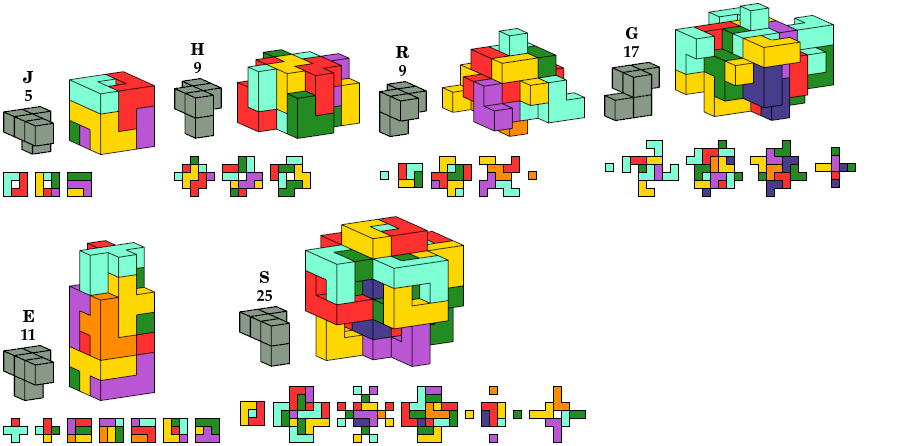
In all pictures, the cross-sections are shown from top to bottom.
If you find a smaller solution, please write.
Bryce Herdt improved on one of my solutions.
Thanks to Joyce Michel for suggesting improvements to this page.
For other classes of symmetry, see:
Nomenclature
Orthogonal 4-Rotary Symmetry
Orthogonal 4-rotary symmetry is the symmetry of 90° rotation
about an axis perpendicular to some faces of the cells.
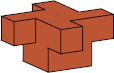
The smallest example of a polycube with orthogonal 4-rotary
symmetry and no stronger symmetry
is this dodecacube (12-cube), as found by W. F. Lunnon:
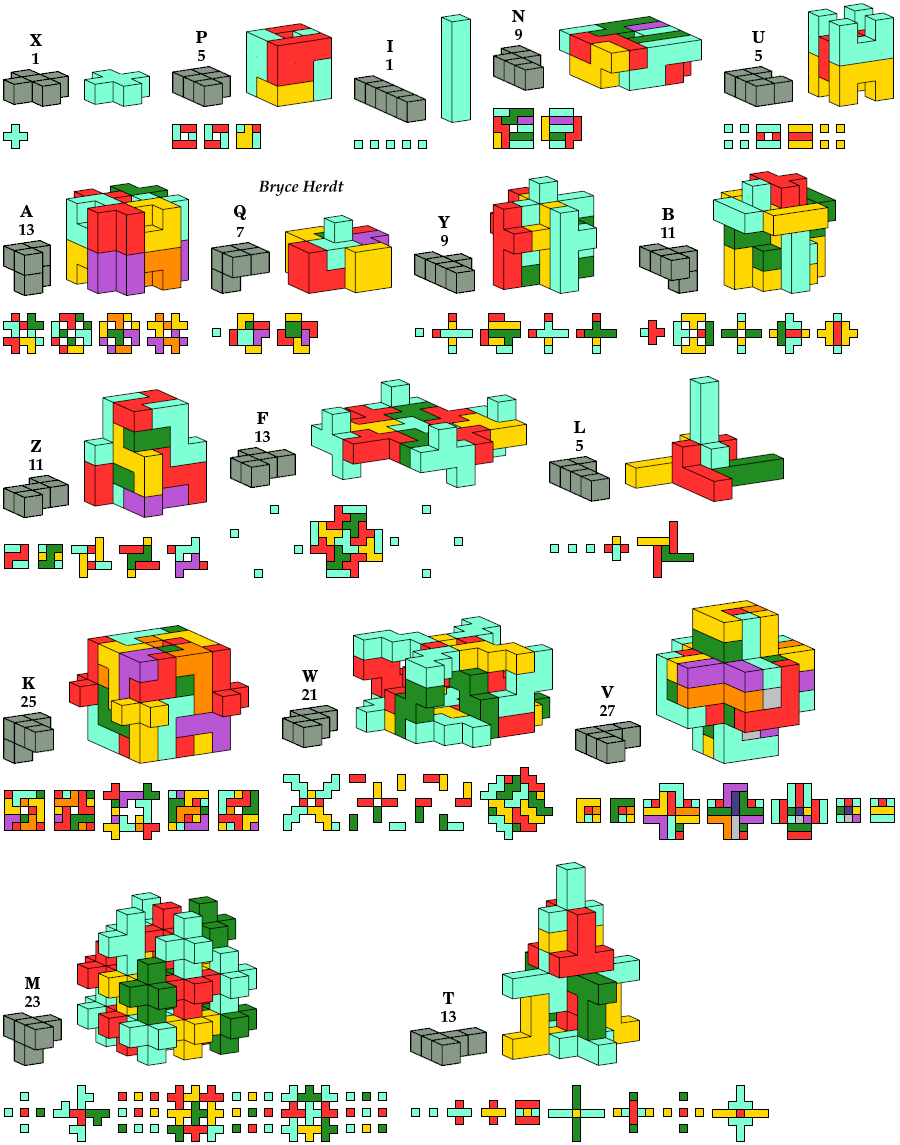
Achiral Pentacubes
The solutions for pentacubes
I and
X
are trivial.
Those pentacubes already have orthogonal 4-rotary symmetry.
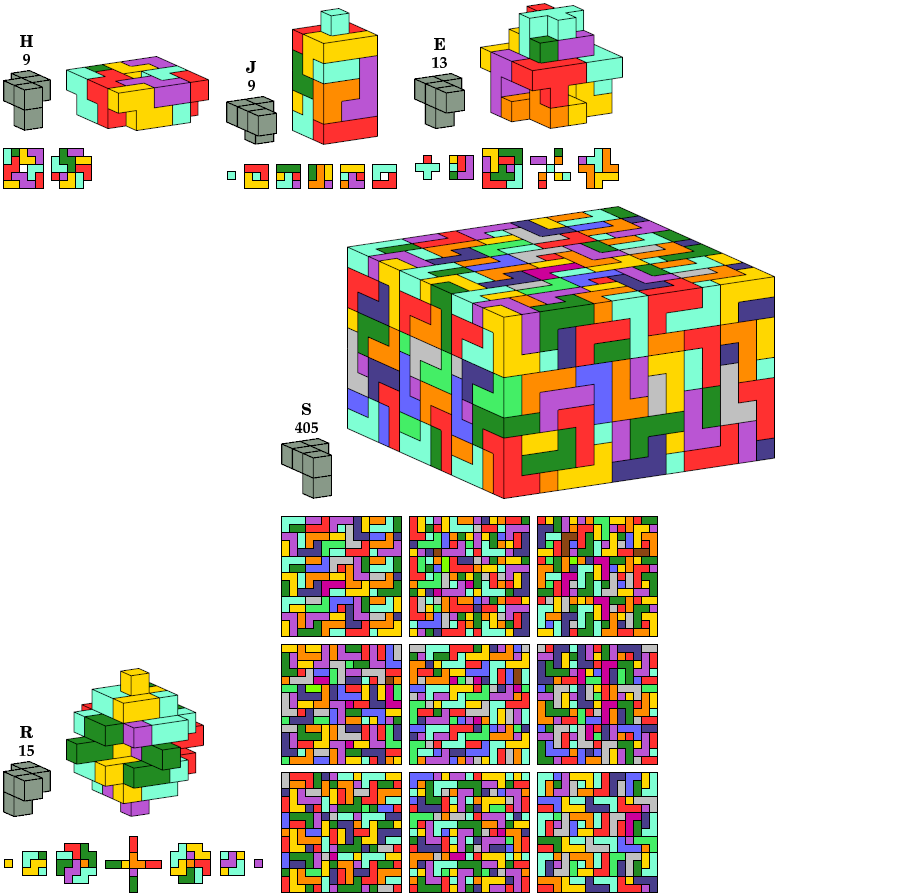
Chiral, Disallowing Reflection
The oddity for the S pentacube
is formed by joining three minimal odd boxes.
No smaller solution is known.
Unsolved
Chiral, Allowing Reflection
Last revised 2026-02-15.
Back to Polyform Oddities
<
Polyform Curiosities
Col. George Sicherman
[ HOME
| MAIL
]






