Tetrahex-Pentahex Oddities
A polyhex oddity
is a symmetrical figure formed by an odd number of copies of
a polyhex.
Symmetrical figures can also be formed with copies of two
different polyhexes.
Since a tetrahex has 4 cells and pentahex has 5,
I use an odd number of cells rather than an odd number of tiles.
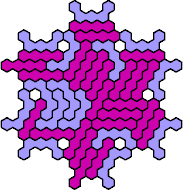
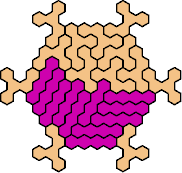
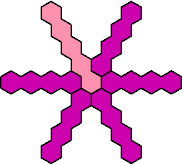
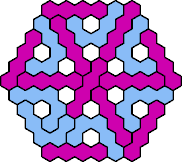
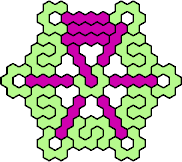
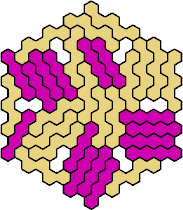
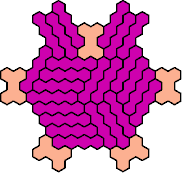
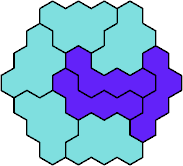
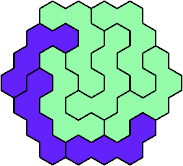
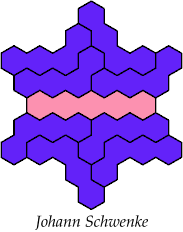
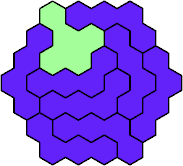
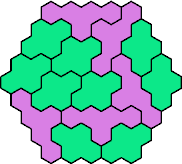
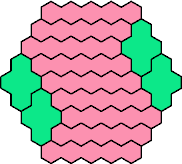
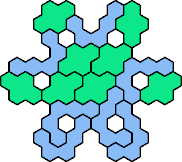
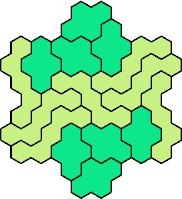
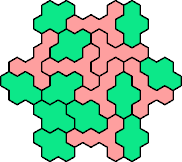
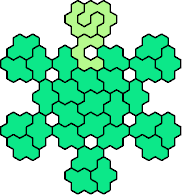
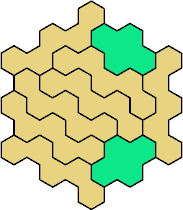
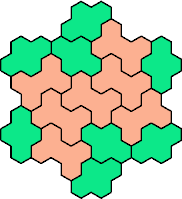
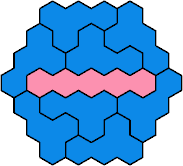
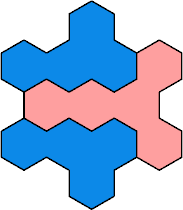
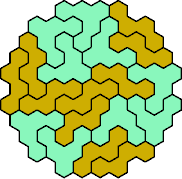
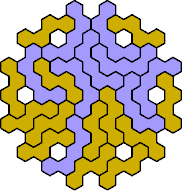
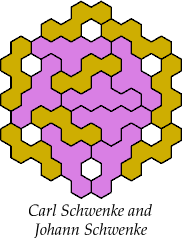
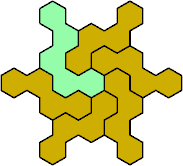
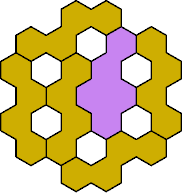
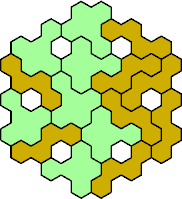
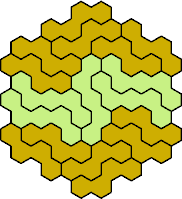
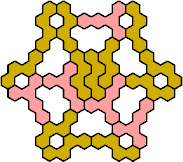
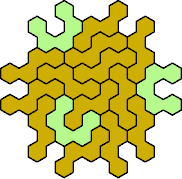
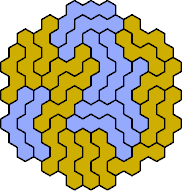
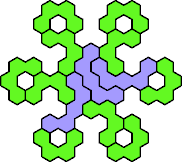
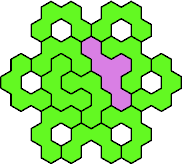
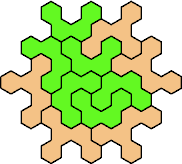
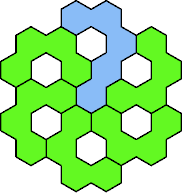
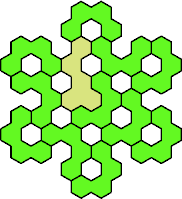
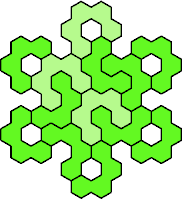
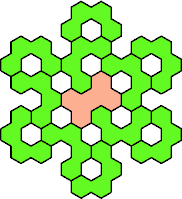
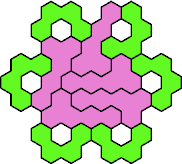
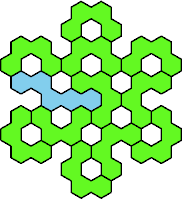
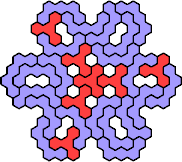
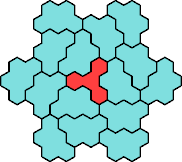
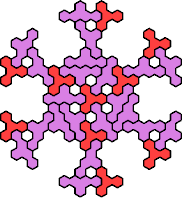
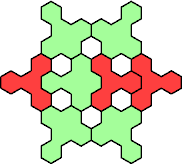
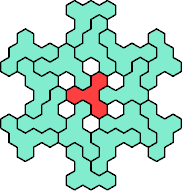
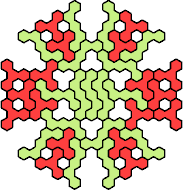
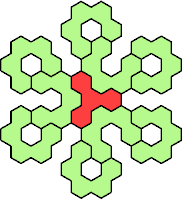
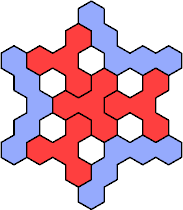
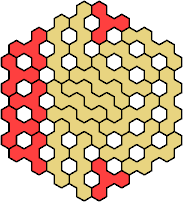
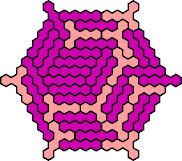
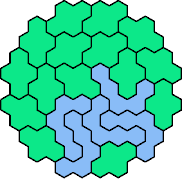
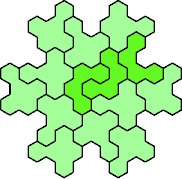
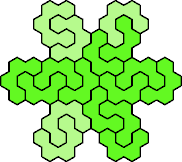
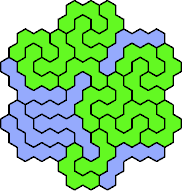
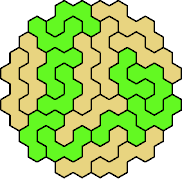
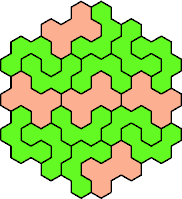
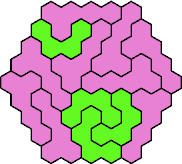
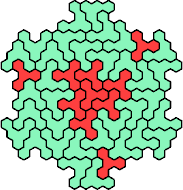
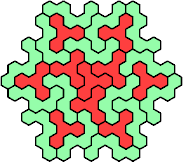
Here are the smallest known fully symmetric polyhexes with an odd
number of cells, formed by copies of a given tetrahex and pentahex,
using at least one of each.
See also
Tetromino-Pentomino Oddities,
Pentomino Pair Oddities,
Hexiamond Pair Oddities,
Pentahex Pair Oddities,
and Trihex-Pentahex Oddities.
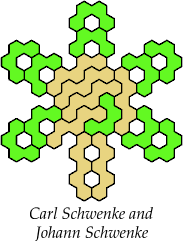
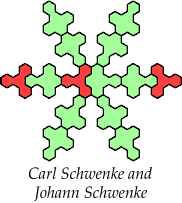
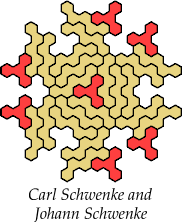
Johann Schwenke improved on some of my solutions.
Chronology of Solutions
[CHRONOLOGY]
| 4I+5A 85 | 4I+5C 175 | 4I+5D 37 | 4I+5E 61 | 4I+5F 85 |
|---|

| 
| 
| 
| 
|
| 4I+5H 109 | 4I+5I 25 | 4I+5J 79 | 4I+5K 85 | 4I+5L 49 |
|---|
| 
| 
| 
| 
|
| 4I+5N 37 | 4I+5P 37 | 4I+5Q 85 | 4I+5R 61 | 4I+5S 121 |
|---|

| 
| 
| 
| 
|
| 4I+5T 109 | 4I+5U 121 | 4I+5V 61 | 4I+5W 145 | 4I+5X 121 |
|---|

| 
| 
| 
| 
|
| 4I+5Y 37 | 4I+5Z 79 | 4J+5A 37 | 4J+5C 37 | 4J+5D 37 |
|---|

| 
| 
| 
| 
|
| 4J+5E 37 | 4J+5F 37 | 4J+5H 37 | 4J+5I 37 | 4J+5J 37 |
|---|

| 
| 
| 
| 
|
| 4J+5K 37 | 4J+5L 37 | 4J+5N 37 | 4J+5P 37 | 4J+5Q 37 |
|---|

| 
| 
| 
| 
|
| 4J+5R 37 | 4J+5S 37 | 4J+5T 37 | 4J+5U 37 | 4J+5V 37 |
|---|

| 
| 
| 
| 
|
| 4J+5W 37 | 4J+5X 37 | 4J+5Y 37 | 4J+5Z 37 | 4O+5A 91 |
|---|

| 
| 
| 
| 
|
| 4O+5C 55 | 4O+5D 31 | 4O+5E 61 | 4O+5F 55 | 4O+5H 55 |
|---|

| 
| 
| 
| 
|
| 4O+5I 61 | 4O+5J 67 | 4O+5K 55 | 4O+5L 37 | 4O+5N 55 |
|---|
| 
| 
| 
| 
|
| 4O+5P 31 | 4O+5Q 31 | 4O+5R 61 | 4O+5S 67 | 4O+5T 79 |
|---|

| 
| 
| 
| 
|
| 4O+5U 127 | 4O+5V 19 | 4O+5W 43 | 4O+5X 67 | 4O+5Y 55 |
|---|
| 
| 
| 
| 
|
| 4O+5Z 55 | 4Q+5A 31 | 4Q+5C 25 | 4Q+5D 31 | 4Q+5E 25 |
|---|

| 
| 
| 
| 
|
| 4Q+5F 31 | 4Q+5H 31 | 4Q+5I 37 | 4Q+5J 37 | 4Q+5K 25 |
|---|

| 
| 
| 
| 
|
| 4Q+5L 37 | 4Q+5N 19 | 4Q+5P 19 | 4Q+5Q 13 | 4Q+5R 31 |
|---|

| 
| 
| 
| 
|
| 4Q+5S 13 | 4Q+5T 13 | 4Q+5U 37 | 4Q+5V 37 | 4Q+5W 37 |
|---|

| 
| 
| 
| 
|
| 4Q+5X 37 | 4Q+5Y 37 | 4Q+5Z 37 | 4S+5A 85 | 4S+5C 97 |
|---|

| 
| 
| 
| 
|
| 4S+5D 31 | 4S+5E 67 | 4S+5F 25 | 4S+5H 55 | 4S+5I 103 |
|---|

| 
| 
| 
| 
|
| 4S+5J 55 | 4S+5K 25 | 4S+5L 61 | 4S+5N 31 | 4S+5P 25 |
|---|

| 
| 
| 
| 
|
| 4S+5Q 67 | 4S+5R 31 | 4S+5S 73 | 4S+5T 73 | 4S+5U 67 |
|---|
| 
| 
| 
| 
|
| 4S+5V 109 | 4S+5W 55 | 4S+5X 67 | 4S+5Y 55 | 4S+5Z 49 |
|---|
| 
| 
| 
| 
|
| 4U+5A 13 | 4U+5C 55 | 4U+5D 37 | 4U+5E 49 | 4U+5F 49 |
|---|

| 
| 
| 
| 
|
| 4U+5H 49 | 4U+5I 13 | 4U+5J 25 | 4U+5K 49 | 4U+5L 37 |
|---|
| 
| 
| 
| 
|
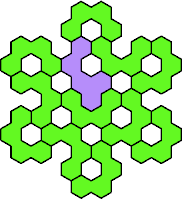
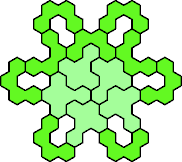
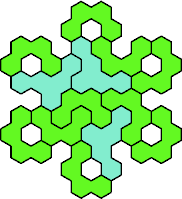
| 4U+5N 49 | 4U+5P 31 | 4U+5Q 61 | 4U+5R 55 | 4U+5S 49 |
|---|
| 
| 
| 
| 
|
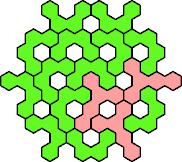
| 4U+5T 67 | 4U+5U 55 | 4U+5V 61 | 4U+5W 79 | 4U+5X 49 |
|---|
| 
| 
| 
| 
|
| 4U+5Y 49 | 4U+5Z 49 | 4Y+5A 109 | 4Y+5C 133 | 4Y+5D 79 |
|---|
| 
| 
| 
| 
|
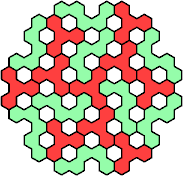
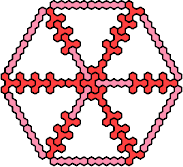
| 4Y+5E 145 | 4Y+5F 85 | 4Y+5H 55 | 4Y+5I 175 | 4Y+5J 19 |
|---|
| 
| 
| 
| 
|
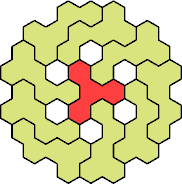
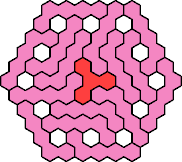
| 4Y+5K 49 | 4Y+5L 79 | 4Y+5N 19 | 4Y+5P 19 | 4Y+5Q 37 |
|---|
| 
| 
| 
| 
|
| 4Y+5R 79 | 4Y+5S 157 | 4Y+5T 25 | 4Y+5U 49 | 4Y+5V 31 |
|---|
| 
| 
| 
| 
|
| 4Y+5W 103 | 4Y+5X 31 | 4Y+5Y 91 | 4Y+5Z 79 |
|---|
| 
| 
| 
|
Solutions shown above that are holeless are not shown here.
| 4I+5C 217 | 4I+5F 121 | 4I+5J 85 | 4I+5L 61 | 4I+5S 169 |
|---|

| 
| 
| 
| 
|
| 4I+5T 175 | 4I+5U 259 | 4I+5W 151 | 4O+5J 85 | 4O+5N 61 |
|---|
| 
| 
| 
| 
|
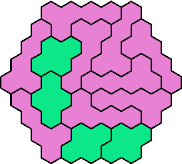
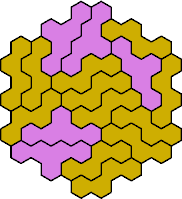
| 4O+5U 193 | 4O+5Y 61 | 4Q+5A 37 | 4S+5C — | 4S+5E 73 |
|---|

| 
| 
| 
| 
|
| 4S+5I 109 | 4S+5J 85 | 4S+5K 55 | 4S+5P 31 | 4S+5Q — |
|---|

| 
| 
| 
| 
|
| 4S+5T 103 | 4S+5X 73 | 4S+5Z 55 | 4U+5C 115 | 4U+5E 91 |
|---|

| 
| 
| 
| 
|
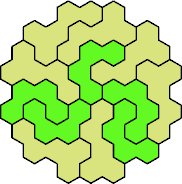
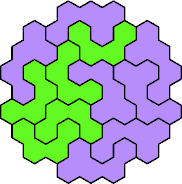
| 4U+5F 55 | 4U+5J 85 | 4U+5K 55 | 4U+5N 55 | 4U+5Q 67 |
|---|

| 
| 
| 
| 
|
| 4U+5R 73 | 4U+5S 109 | 4U+5T 133 | 4U+5U 73 | 4U+5V 103 |
|---|

| 
| 
| 
| 
|
| 4U+5W 85 | 4U+5X 73 | 4U+5Y 61 | 4U+5Z 73 | 4Y+5A 205 |
|---|
| 
| 
| 
| 
|
| 4Y+5C — | 4Y+5E 217 | 4Y+5F 115 | 4Y+5I — | 4Y+5K 91 |
|---|

| 
| 
| 
| 
|
| 4Y+5L 85 | 4Y+5Q 67 | 4Y+5R 121 | 4Y+5S 433 | 4Y+5T 31 |
|---|

| 
| 
| 
| 
|
| 4Y+5U 115 | 4Y+5V 97 | 4Y+5W 133 | 4Y+5Z 109 |
|---|
| 
| 
| 
|
Last revised 2024-10-09.
Back to Polyform Oddities
<
Polyform Curiosities
Col. George Sicherman
[ HOME
| MAIL
]












































































































































































































