
Oddities can also be constructed from sets of different shapes. Here are the minimal known oddities for triplets of tetrapents, using at least one copy of each tetrapent. Please write if you find a smaller solution or solve an unsolved case.
See also Tetrapent Oddities and Tetrapent Pair Oddities.
| Tiles | Triplets |
|---|---|
| 3 | 21 |
| 5 | 14 |

| Tiles | Triplets |
|---|---|
| 3 | 1 |
| 5 | 29 |
| 7 | 4 |
| — | 1 |
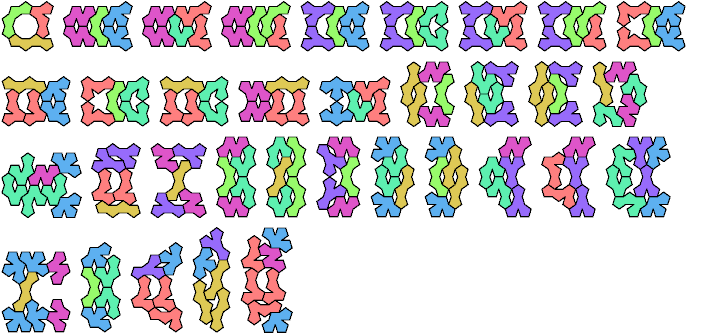

| Tiles | Triplets |
|---|---|
| 3 | 5 |
| 5 | 30 |

| Tiles | Triplets |
|---|---|
| 5 | 14 |
| 7 | 13 |
| 9 | 5 |
| 11 | 1 |
| 13 | 1 |
| — | 1 |


| Tiles | Triplets |
|---|---|
| 25 | 10 |
| 35 | 15 |
| 45 | 4 |
| 65 | 1 |
| — | 1 |
| ? | 4 |



Last revised 2023-11-13.