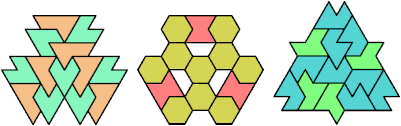
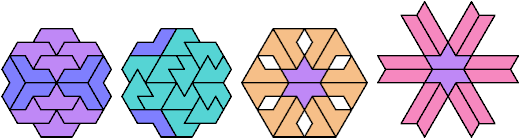
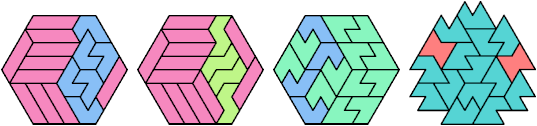
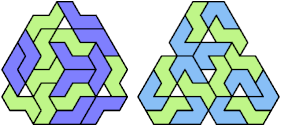
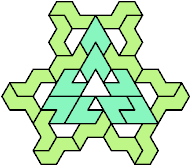
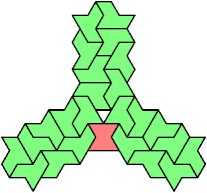
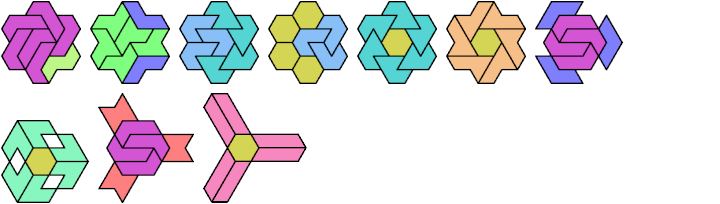
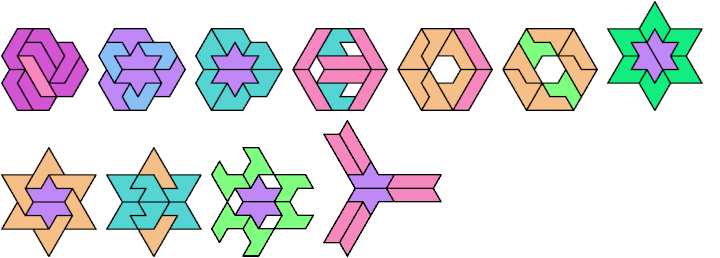
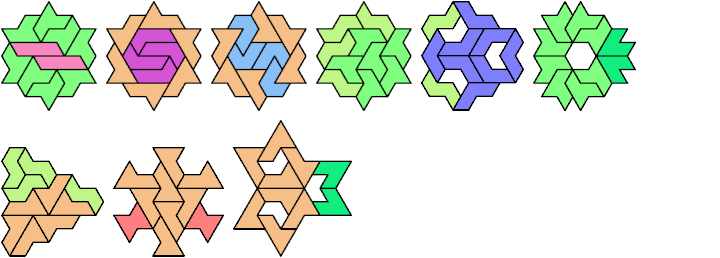
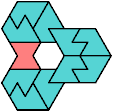
A tri-oddity is an arrangement of a number of copies of a polyform, not a multiple of 3, with ternary symmetry. It is a variant of an oddity.
Many polyforms cannot have ternary symmetry. Polyiamonds can, along with polyhexes and polycubes.
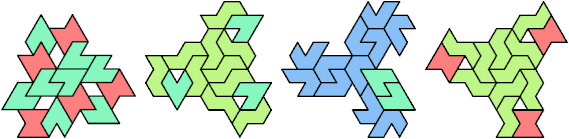
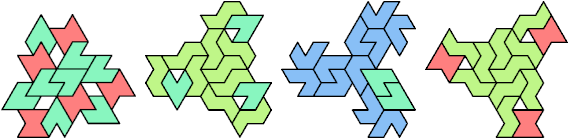
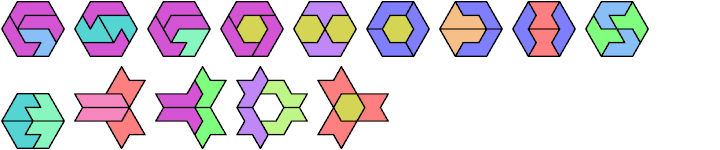
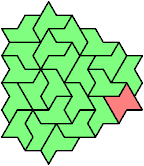
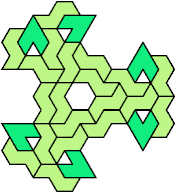
Here I show minimal known tri-oddities formed by copies of two hexiamonds, using at least one of each. If you find a smaller solution, or solve an unsolved case, please let me know.
| A | E | F | H | I | L | O | P | S | U | V | X | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | * | 5 | 4 | 8 | — | 4 | 4 | 10 | 13 | 13 | — | 13 |
| E | 5 | * | 5 | 5 | 5 | 5 | 4 | 5 | 5 | 5 | 5 | 5 |
| F | 4 | 5 | * | 7 | 7 | 4 | 4 | 5 | 8 | 7 | 7 | 11 |
| H | 8 | 5 | 7 | * | 10 | 4 | 4 | 7 | 7 | 4 | 7 | 10 |
| I | — | 5 | 7 | 10 | * | 7 | 4 | 4 | 8 | 8 | — | 4 |
| L | 4 | 5 | 4 | 4 | 7 | * | 4 | 5 | 7 | 2 | 7 | 7 |
| O | 4 | 4 | 4 | 4 | 4 | 4 | * | 4 | 4 | 4 | 4 | 4 |
| P | 10 | 5 | 5 | 7 | 4 | 5 | 4 | * | 4 | 4 | 4 | 7 |
| S | 13 | 5 | 8 | 7 | 8 | 7 | 4 | 4 | * | 7 | 7 | 13 |
| U | 13 | 5 | 7 | 4 | 8 | 2 | 4 | 4 | 7 | * | 5 | 8 |
| V | — | 5 | 7 | 7 | — | 7 | 4 | 4 | 7 | 5 | * | 4 |
| X | 13 | 5 | 11 | 10 | 4 | 7 | 4 | 7 | 13 | 8 | 4 | * |


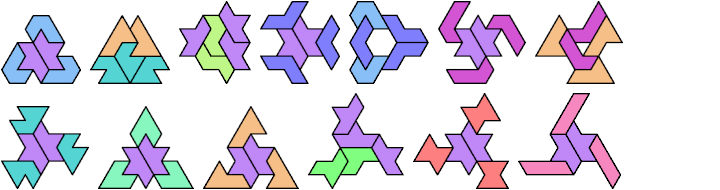
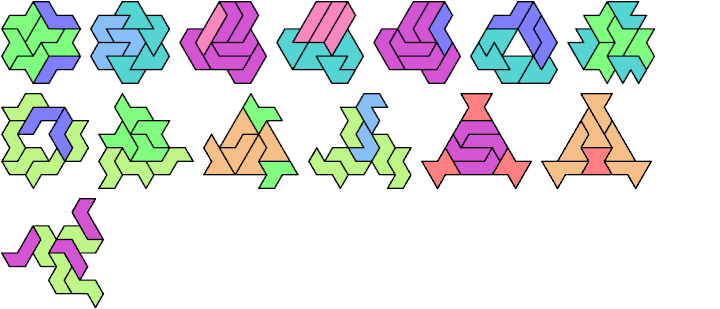
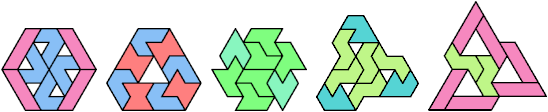
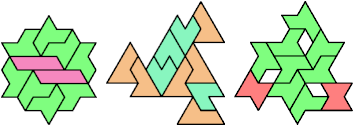

| A | E | F | H | I | L | O | P | S | U | V | X | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | * | 5 | 4 | 8 | — | 4 | 4 | 10 | 16 | 13 | — | ? |
| E | 5 | * | 5 | 5 | 5 | 5 | 4 | 5 | 5 | 5 | 5 | 5 |
| F | 4 | 5 | * | 7 | 7 | 4 | 4 | 5 | 10 | 7 | 11 | 16 |
| H | 8 | 5 | 7 | * | 10 | 4 | 4 | 7 | 7 | 4 | 7 | 14 |
| I | — | 5 | 7 | 10 | * | 7 | 4 | 4 | 13 | 13 | — | 4 |
| L | 4 | 5 | 4 | 4 | 7 | * | 4 | 7 | 7 | 4 | 7 | 7 |
| O | 4 | 4 | 4 | 4 | 4 | 4 | * | 4 | 4 | 4 | 4 | 4 |
| P | 10 | 5 | 5 | 7 | 4 | 7 | 4 | * | 4 | 4 | 4 | 7 |
| S | 16 | 5 | 10 | 7 | 13 | 7 | 4 | 4 | * | 7 | 10 | 19 |
| U | 13 | 5 | 7 | 4 | 13 | 4 | 4 | 4 | 7 | * | 7 | 10 |
| V | — | 5 | 11 | 7 | — | 7 | 4 | 4 | 10 | 7 | * | 4 |
| X | ? | 5 | 16 | 14 | 4 | 7 | 4 | 7 | 19 | 10 | 4 | * |

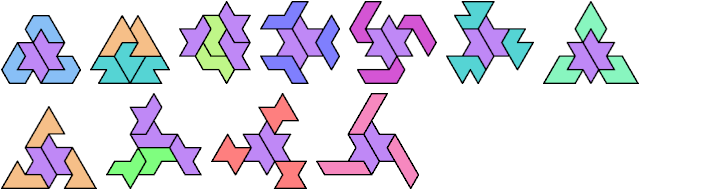


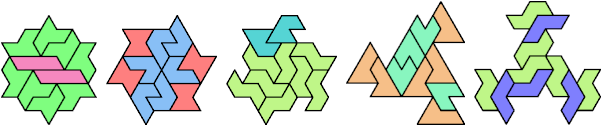

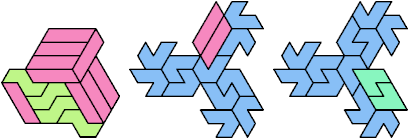
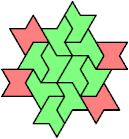
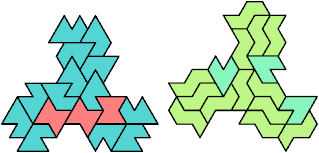
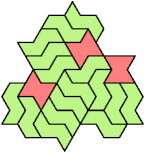
| A | E | F | H | I | L | O | P | S | U | V | X | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | * | 5 | 4 | 8 | — | 4 | 7 | 13 | 23 | 16 | — | ? |
| E | 5 | * | 8 | 8 | 14 | 10 | 4 | 14 | 10 | 8 | 14 | ? |
| F | 4 | 8 | * | 13 | 10 | 4 | 7 | 5 | 10 | 7 | 14 | 16 |
| H | 8 | 8 | 13 | * | 10 | 7 | 7 | 10 | 10 | 4 | 7 | 25 |
| I | — | 14 | 10 | 10 | * | 8 | 10 | 7 | 16 | 16 | — | ? |
| L | 4 | 10 | 4 | 7 | 8 | * | 4 | 10 | 7 | 2 | 11 | 7 |
| O | 7 | 4 | 7 | 7 | 10 | 4 | * | 7 | 7 | 7 | 4 | 13 |
| P | 13 | 14 | 5 | 10 | 7 | 10 | 7 | * | 7 | 7 | 4 | 7 |
| S | 23 | 10 | 10 | 10 | 16 | 7 | 7 | 7 | * | 17 | 17 | ? |
| U | 16 | 8 | 7 | 4 | 16 | 2 | 7 | 7 | 17 | * | 7 | 8 |
| V | — | 14 | 14 | 7 | — | 11 | 4 | 4 | 17 | 7 | * | 4 |
| X | ? | ? | 16 | 25 | ? | 7 | 13 | 7 | ? | 8 | 4 | * |


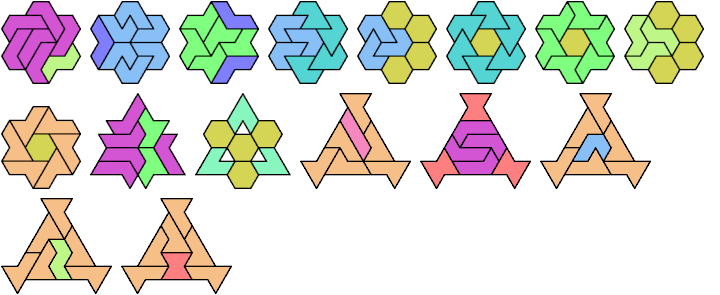

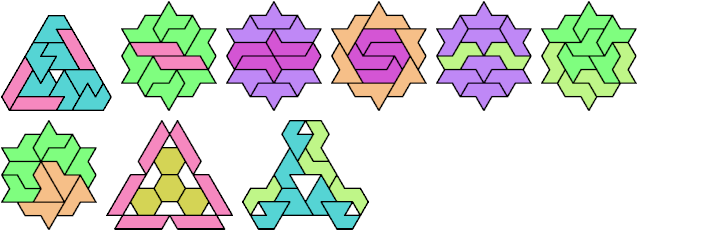

| A | E | F | H | I | L | O | P | S | U | V | X | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | * | 8 | 4 | 10 | — | 4 | 7 | 10 | 26 | 14 | — | ? |
| E | 8 | * | 8 | 8 | 8 | 5 | 4 | 8 | 4 | 8 | 5 | ? |
| F | 4 | 8 | * | 13 | 8 | 4 | 7 | 8 | 16 | 7 | 11 | 11 |
| H | 10 | 8 | 13 | * | 10 | 4 | 5 | 8 | 10 | 4 | 7 | 23 |
| I | — | 8 | 8 | 10 | * | 8 | 7 | 8 | 16 | 16 | — | 4 |
| L | 4 | 5 | 4 | 4 | 8 | * | 4 | 10 | 7 | 4 | 7 | 7 |
| O | 7 | 4 | 7 | 5 | 7 | 4 | * | 7 | 5 | 7 | 4 | 4 |
| P | 10 | 8 | 8 | 8 | 8 | 10 | 7 | * | 10 | 10 | 4 | 10 |
| S | 26 | 4 | 16 | 10 | 16 | 7 | 5 | 10 | * | 13 | 10 | ? |
| U | 14 | 8 | 7 | 4 | 16 | 4 | 7 | 10 | 13 | * | 5 | 16 |
| V | — | 5 | 11 | 7 | — | 7 | 4 | 4 | 10 | 5 | * | 4 |
| X | ? | ? | 11 | 23 | 4 | 7 | 4 | 10 | ? | 16 | 4 | * |

Last revised 2025-02-11.