 |
 |
 |
 |
 |
|
|
to this page of unusual magic stars. New material will be added here as it becomes available and time permits. enjoy! |
 |
Six in Six |
Two order-6 super-imposed magic stars |
Eight in Eight (A) |
Two order-8B super-imposed magic stars |
Eight in Eight (B) |
Two order-8 super-imposed magic stars of patterns A & B |
Five-in-a-row (8) |
An order-8A magic star with 5 numbers per line. |
Five-in-a-row (6) |
Alan B. Johnson, Jr's prime number hexagon. |
Five-in-a-row (6b) |
A magic hexagon with 9 rows of 5 numbers |
Magic Star-Magic Triangles |
Two magic hexagons with 8 magic triangles (1 with prime #) |
Hexagram - magic triangles |
Six stars with small triangles summing the same. |
Multiplying magic hexagram |
Product of the 4 numbers in each line is 1 (Mod 13). |
Five-in-one |
Five order-7 super-imposed magic stars. |
Three Magic Stars in one |
Two stars make one with 8 numbers per row. |
Garrick's 6-in-a-row |
An order-12B using numbers from 1 to 36 sums to 111. |
![]()
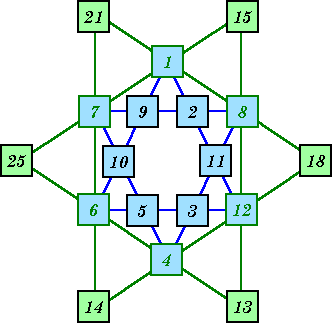
Two order-6 magic stars with some cells common to both.
The blue inner star is basic solution #1 with S = 26.
The green outer star is not a pure magic star because the
numbers are not consecutive. S = 48.
![]()

2 super-imposed order-8 pattern B stars. The small star is a pure
magic star so S = 34. It is solution # 30.
The large star has S = 68
The valley cells are common to both stars although they are in the interior of the large star (not the valleys) .
![]()
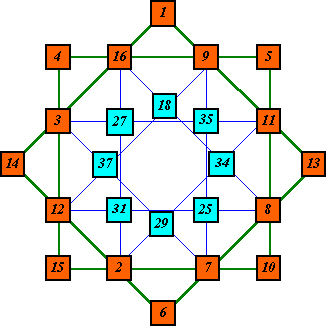
An order-8B star super-imposed over an order-8A star.
The type A star is index #26. The type B star S=76
The valley cells of the type A star are the peak cells of
the type B star.
![]()
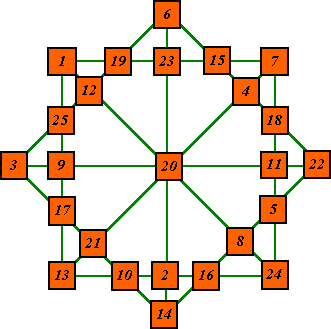 An order-8A type star but contains 12 rows of 5 numbers. Numbers 1-25. S=65.
An order-8A type star but contains 12 rows of 5 numbers. Numbers 1-25. S=65.
This type of star is now known as an Isomorphic magic star.
This pattern has a direct relationship to an order-5 magic square.
This is the pandiagonal magic square I constructed it from.
| 1 | 19 | 23 | 15 | 7 |
| 25 | 12 | 6 | 4 | 18 |
| 9 | 3 | 20 | 22 | 11 |
| 17 | 21 | 14 | 8 | 5 |
| 13 | 10 | 2 | 16 | 24 |
![]()
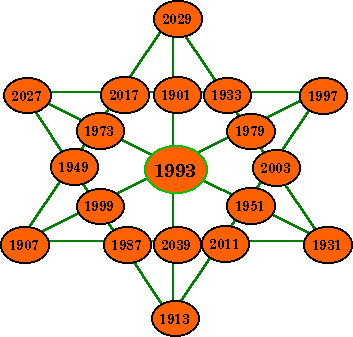
This magic hexagon commemorates the year 1993.
It consists of the 13 prime years of the 20th century and
the first six prime years of the 21st century. Each line of
five primes sum to the constant 9875.
It was designed by Alan Wm. Johnson. Jr. and appeared
in Recreational & Educational Computing Newsletter,
Dec. 1992, vol. 7, No. 8.
See the REC homepage at http://members.aol.com/DrMWEcker/REC.html
See other material from REC .
Use Back button to return)
![]()
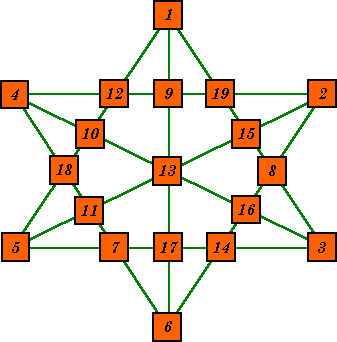 |
This star contains the consecutive numbers 1 to 19 in 9 rows of 5 numbers. Each row sums to 46. |
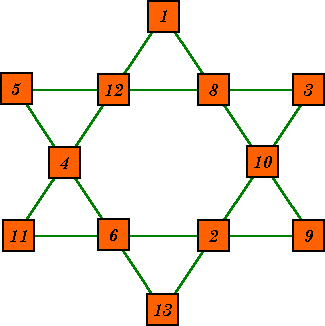 |
This magic hexagon uses the numbers 1 to 13 to form 6 lines summing to 28. Each of the six small triangles of 3 numbers, as well as the two large triangle points, sum to 21. Because the number seven is missing, this is not a pure magic star. |
 |
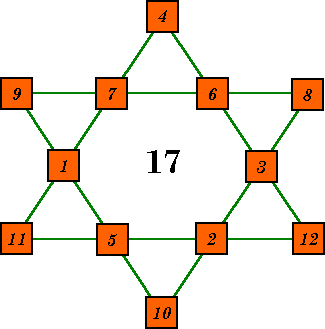
This magic hexagon uses 12 prime numbers to form 6 lines summing to 308. Each of the six small triangles of 3 numbers, as well as the two large triangle points, sum to 231.
Both of these stars from Harry Langman, Ph.D., Play Mathematics, Hafner Publishing Co. 1962. |
![]()
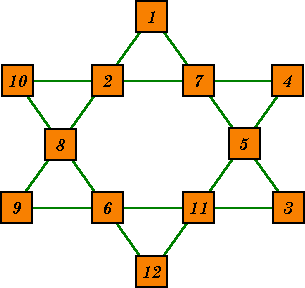
 |
This star contains the consecutive numbers 1 to 12 arranged so that all six small triangles sum to 17. The complement of this star (each
number There are two other such arrangements, Note that the star, as a whole, is not magic. From Harry Langman, Ph.D., Play Mathematics, Hafner Publishing Co. 1962. |
 |
When the four numbers in each line are multiplied together, the product, when divided by 13, leaves a remainder of one. This pattern was designed by David M. Collison (1937-1991). |
![]()
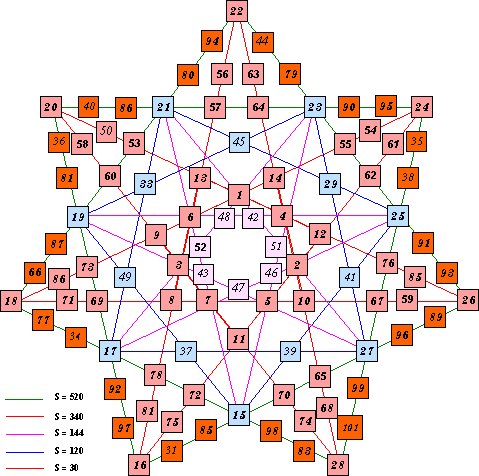 This pattern was constructed by a Mr. Morton about 1915. It appears as fig.
678 on page 348 of W. S. Andrews, Magic Squares and Cubes, Dover Publ. 1960
This pattern was constructed by a Mr. Morton about 1915. It appears as fig.
678 on page 348 of W. S. Andrews, Magic Squares and Cubes, Dover Publ. 1960
The innermost star (heavy red) is an upside-down Pattern 7A, and uses the consecutive numbers from 1 to 14 so is a pure magic star. It is an equivalent to basic solution number 71.
The blue star (S = 120) also has 4 numbers per line. It is also an upside down Pattern 7A.
The Violet star (S = 144) has 6 numbers per line and is an upside down pattern 7B.
The light red star (S = 340) has 10 numbers per line and is also a pattern 7B.
The Green outside star (S = 520) also has 10 numbers per line and is a pattern 7A.
The author used the numbers from 1 to 101 for this construction. Six of these numbers were not used and three of them were used twice. Can you find these missing and duplicate numbers?
![]()
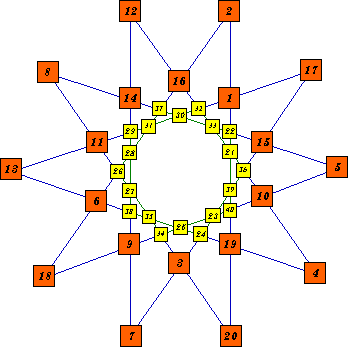 |
On examining the patterns of some higher order magic stars, we see that the inner part of the pattern is actually another pattern for the same order. By adding 2n to each number of a basic star of that order we obtain a new magic star. To the left I show an order-10 pattern C star. The outside 20 numbers form the basic solution 5304 (the first one with a = 2) and the magic sum 42. The inside part of the pattern is order-10 pattern A. Here it forms a magic star with the consecutive numbers from 21 to 40. These were obtained by adding 20 to each number of the basic solution (also # 5304) of pattern A. This star has the magic sum of 122. The entire pattern forms a magic star with 8 numbers per line and the magic constant 164. |
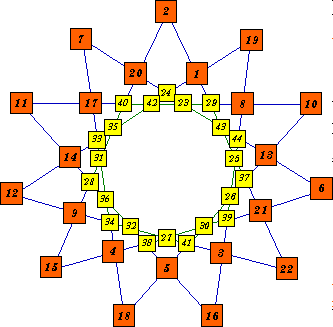 |
The order-11 star is pattern C with pattern A inside. The overall
pattern uses consecutive numbers from 1 to 44. Magic sums are S = 46, S = 134, S = 180 Index numbers are 11-C # 27224 and 11-A # 26306. A similar star can be constructed using 12C with 12A inside. Similar patterns could be made using 9A with 9C inside, 11B with 11D inside and 12B with 12D inside. In these 3 cases however, the inside star would be very small in comparison with the outside one.
|
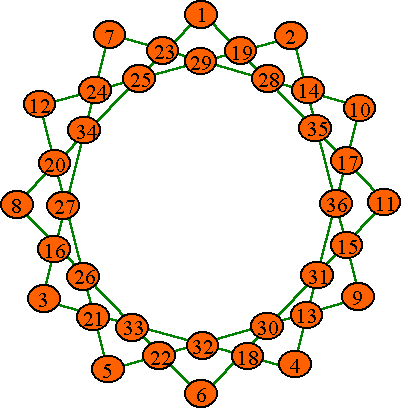 |
This pattern was sent to me on Mar. 5, 2002 by Garrick Wells of Charlotte,
North Carolina, U. S. A.. He reported that it took him 5 1/2 weeks to design it. It is an Order-12, pattern B star, but not standard because it contains more then 4
numbers per line. In addition, the valley numbers form the corners of two overlapping hexigons of 6
numbers each that sum to the same 111. Notice that the 12 lowest numbers appear in the point (peak) positions, the 12 middle
numbers appear in the valleys, and the 12 highest numbers appear in the interior of the
star. |
Please send me Feedback about my Web
site!![]()
![]()

![]()
Harvey Heinz harveyheinz@shaw.ca
This page last updated
March 01, 2005
Copyright © 1998, 1999 by Harvey D. Heinz