 |
 |
 |
 |
 |
Order-5 Isomorphic-magic Star |
The star that started it all (reproduced from my Unusual Magic Stars
page). This is the only order-8 magic star that is fully isomorphic to an order-5 magic square. |
Regular Order-5 |
This star is isomorphic to a regular order-5 magic square. |
Order-7 Pan-magic Star |
This star is a transformation of an order-7 panmagic square. |
Order-9 Isolike magic Stars |
This star is a transformation of an order-9 panmagic and diammagic square. However, it is incomplete, because the main diagonals would require duplicate numbers. |
Order-9 Butterfly Stars |
An order-9 panmagic square transforms to two order-12 magic stars, one with an embedded order-8 magic star. |
Order-13 Isolike magic star |
This star is a transformation of an order-13 diammagic and plusmagic square. |
Comparison of features |
Compares the characteristics of Iso-like, Isomorphic and Pan-magic stars. |
Conclusions and Questions |
A wrap-up, more about plusmagic and diammagic, food for thought. |
On April 30, 1999, I received an e-mail from Aale de Winkel commenting on the
Five-in-a-row(8) magic star located on my Unusual Magic Squares page. This star (which is
reproduced below) is obtained by a transformation of an order-5 pandiagonal magic square
into an order-8B magic star..
This message was the first of an intense exchange of communications between us during the
month of May, as we jointly investigated the properties of this star configuration.
Aale's investigations involve using the pan-diagonals to help form an order-8B magic star.
Hence the name Pan-magic stars. We originally assumed that magic stars of this type are
isomorphic only to pandiagonal magic squares (not regular magic squares).
This investigation also resulted in the discovery (by Aale) of magic squares with various patterns beside the usual rows, columns and diagonals.
My emphasis has been on the formation of type order-8B magic stars using only numbers
from the magic square that will contribute to forming complete magic lines.
My efforts (and the examples here) involve the embedded "plus",
"diamond", "cross" or "ring" patterns and do not necessarily
require the magic square be pandiagonal. I call this type of square a Quadrant Magic
Square.
My special thanks to Aale de Winkel for the use of his pan-magic templates and data
files which permitted me to find suitable magic squares. And for the basic idea to
investigate this subject and include me in his endeavor.
Visit his page on pan-magic stars
which deals in more detail with the transformations.
Some definitions All of these but "isolike"
and "quadrant magic" were coined by Aale de Winkel in May of 1999
These magic arrays are discussed in more detail on my Quadrant Magic Squares page
(see below).
| pan-magic stars | Order-8B star from odd order >5 pandiagonal magic square. See above secton. |
| butterfly star | An order-12 star (points are small) that has 16 or more lines summing correctly. |
| isolike magic star | Order-8B star from odd order >8 quadrant magic square. See above section. |
| incomplete | A isolike magic star has 10 or 12 lines of n numbers summing correctly. n is the order of the magic square. If the 2 main diagonals cannot be made magic (only 10 correct lines), it is an incomplete isolike magic star. |
| diammagic | A magic square that has a diamond formation that sums correctly, in each quadrant. Many of these squares will have diamond formations in other areas as well! |
| plusmagic | A magic square that has a plus formation that sums correctly, in each quadrant. Many of these squares will have plus formations in other areas as well! The order-5 pandiagonal magic square used in my first example has 25 such arrays, one centered around each number of the square. |
| crosmagic | A magic square that has a plus formation that sums correctly, in each quadrant. It is not possible to construct pan-magic stars using this formation. |
| tcrosmagic | A form of 'thick' cross that appears in order-17 magic squares.Not usable for pan-magic star construction. |
| sringmagic | A ring of n-1 numbers around the central number of each quadrant. These, plus the central number, sum to the constant. It is not possible to construct pan-magic stars using this formation. |
| lringmagic | As sringmagic except there is a gap of 1 number between each number of the ring. It is not possible to construct pan-magic stars from order-9 magic squares using this formation. However, it is possible with order-17 magic squares that have this feature. |
| quadrant magic squares | Magic squares of any order 4n + 1 that contain any of the above
six features (all discovered by Aale de Winkel). While any given feature must appear in
all 4 quadrants, it is quite possible that this feature will also appear in other areas of
the magic square. It is also possible for a magic square to contain more then one of these
features. These magic arrays are discussed in more detail on my Quadrant Magic Squares page. |
![]()
Order-5 is the only order magic square that can form a fully isomorphic magic star because there are 25 numbers in the order-5 magic square and 25 numbers in a complete order-5 isolike magic star.
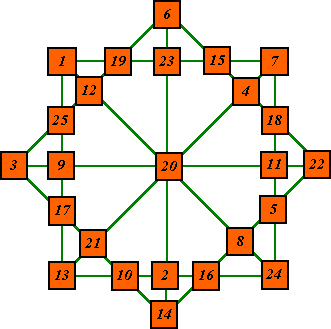 |
This star is formed from the magic square below according to the template
below,left. This template can be used to form such a star from any order-5 pandiagonal
magic square. Plusmagic |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
This star (below) is constructed from a normal (not pandiagonal), associative order-5 magic square.
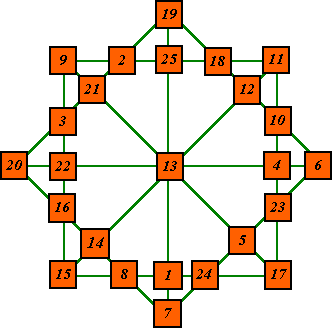 |
This square also is plusmagic, but only in the quadrants. Notice that the outside diagonals are each formed from one of these 'plus' arrays. The template above was used for this star also. |
| The order-8 stars shown below are formed from this order-7 pandiagonal
magic square. Note the four lighter colored cells in the two stars below. This is caused because the corner numbers in the square must appear in 4 different
lines; the row, the column, the diagonal and a pan-diagonal. Because the outside diagonals are formed from a pandiagonal, these are pan-magic stars. Because order-7 magic squares cannot be plusmagic or diammagic, an isolike magic star is impossible. |
|
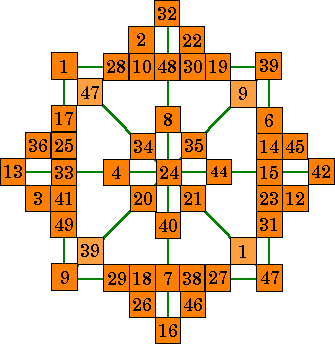 |
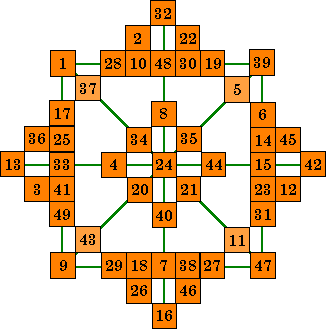 |
| A. This star is magic in all 12 lines but 4 of the 49 numbers are
not used and 4 numbers are duplicated. |
B. This star uses all 49 numbers (with no duplicates), but only 8 lines sum correctly. The four diamond lines (corners 32, 42, 16 and 13) do not. This is NOT a magic star. |
|
Template notes The numbers in these templates are coordinates in the relevant magic square. This template is adapted from Aale de Winkel's isomorphic star order 8(27P8(2,3)a) to create the stars above. To save space, I have not included the brackets that would normally appear around each number. |
![]()
As explained for the order-7, an order-9 pandiagonal magic square cannot form an order-8 magic star without duplicating the corner numbers. However, there is a special kind of order-9 pandiagonal that has embedded formations of 9 cells.Aale de Winkel has labeled them diammagic (diamond magic) squares. These cells are highlighted in the top left quadrant of the square used to construct this magic star.
Iso_9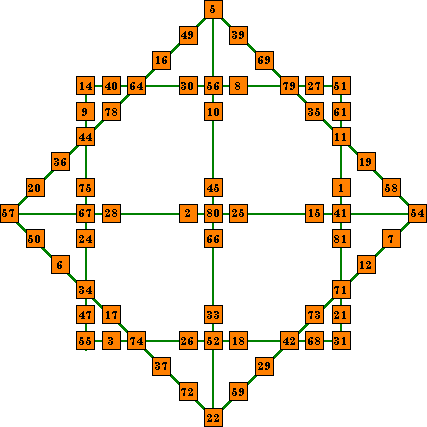 |
This order-8 magic star contains ten lines of nine numbers. It uses 65 of the 81 numbers from the magic square and contains no duplicate numbers. An isolike magic star must also have the two main diagonal lines also, for a total of 12 correct lines, with no numbers duplicated. It is impossible to form these diagonal lines from a diammagic square without requiring duplicate numbers. Iso_9 is, therefore, an incomplete isolike magic star.
|
|
The highlighted cells in the upper left diammagic square above, form the
top left skew line. A similar array in each of the other quadrants form the other 3 skew
lines. Because the 36 and the 16 also appear in the main diagonal, the two diagonals
cannot be included without requiring duplicate numbers. The Iso_9 star therefore has only
10 correct lines and cannot be considered complete. The template shown here may be used with any order-9 magic square that is diammagic. If there are any order-9 plusmagic squares, they could be used to form a complete isolike magic star. |
The overall pattern is an order-12 butterfly magic star. It is order-12 because of the 12 (small) points.
The first example (butterfly A.) contains 20 correct lines of 9 numbers with each
summing to 369.
It uses all 81 of the original numbers from the square. However, four of these numbers
appear twice.
It must be constructed from a pandiagonal order-9 magic square.
Embedded is an order–8 type A star (heavy green lines and slightly darker
cells).
Notice that the line 3 to 25 of the embedded star is composed of the pan-diagonal pair 43
- 66 and 77 of the magic square.
The 77 already appears in a row, column, and main diagonal, and so must be duplicated to
complete this line.
I have moved the green (duplicate) numbers off of the main diagonals as shown in de Winkel's template. This results in the main diagonals now also being correct, but at the cost of a loss in symmetry.
Butterfly A.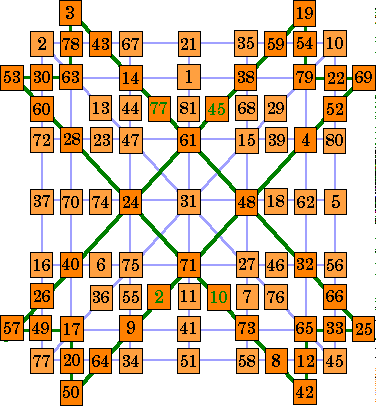 |
This is the pandiagonal magic square used for these butterfly stars. It is
diammagic but this feature is not used in this type of magic star.
|
|
This template was received from Aale de Winkel May 13/99, his (29P12(1,2)). For the Butterfly A. star, the duplicate (green) numbers have been moved off of the main diagonals. This makes these diagonals sum correctly, but the star is no longer symmetrical.
|
 |
Butterfly B. This pattern is an order-12
butterfly magic star quite similar to the above (Butterfly A.) magic star. It may be constructed from any order-9 magic square (not necessarily
pandiagonal). It uses all 81 of the original numbers from the square. The same template is used as for the other magic star. The duplicate (green) numbers have been removed, as have the blank rows & columns. There is no longer an embedded order-8 magic star. |
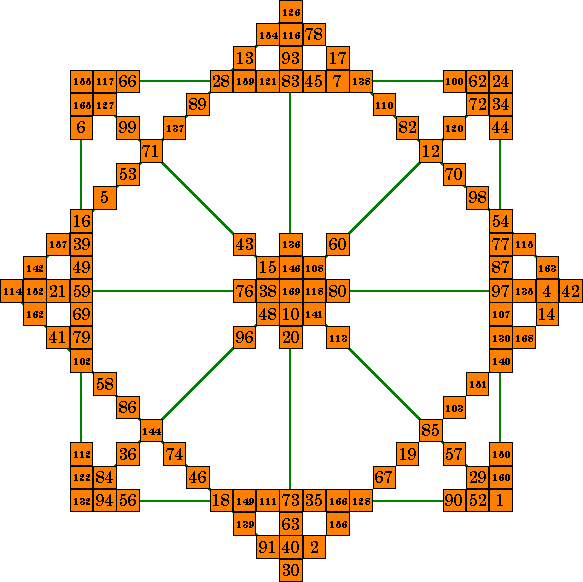 |
This magic star is constructed from an order-13 diammagic
square. It consists of 12 lines of 13 numbers that all sum to 1105. It uses 107 of the 169 numbers in the magic square, and requires no duplicate numbers With 12 correct lines and no duplicate numbers, it is considered complete. Only magic squares of orders 8m-3 (such as 5, 13, 21, etc) can form complete isolike magic stars (unless there are plusmagic squares of order 8m+1). In this diagram the 3 digit numbers are as large as possible. I left the 2 digit ones larger for better eligibility. |
This is a pandiagonal diammagic, plusmagic square of order-13.
|
It contains magic diamond arrays in each quadrant such as the one
highlighted (centered around the number 71) and is therefore diammagic. These four arrays form the four outer diagonal lines of the magic star above. This same square, however, is also plusmagic. It contains arrays in each quadrant similar to the one highlighted in the upper right corner. A different magic star could be formed from members of these arrays by substituting the
necessary 8 numbers in each of the four outside diagonals of the above star. |
Finally, this square is sringmagic and crossmagic, as shown in the lower two quadrants. However, these features are of no value to the formation of isolike magic stars. The sringmagic has 2 extra cells on the quadrant diagonal (in addition to the center cell). The crosmagic array has one one of the lines of the cross always falling on a main diagonal. This makes it impossible to form the main diagonals of the star without requiring duplicate numbers.
The four lime colored cells above are the center cells of each array.
The other cells in each pattern are arranged symmetrically around them.
The center row and center column of the quadrant magic square is common to 2 adjacent quadrants. This means that for most arrays, there are numbers that are common to two adjacent arrays.
Conditions necessary for transformation of a quadrant magic square to an iso-like magic star.
![]()
For sake of completeness, I show the template for this order-13 pan-magic star.
| 3,6 | ||||||||||||||||||||||||
| 2,5 | 2,6 | 2,7 | ||||||||||||||||||||||
| 1,4 | 1,6 | 1,8 | ||||||||||||||||||||||
| 0,0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 0,10 | 0,11 | 0,12 | ||||||||||||
| 1,0 | 1,1 | 1,2 | 1,10 | 1,11 | 1,12 | |||||||||||||||||||
| 2,0 | 2,2 | 2,1 | 2,11 | 2,10 | 2,12 | |||||||||||||||||||
| 3,3 | 3,9 | |||||||||||||||||||||||
| 5,4 | 5,8 | |||||||||||||||||||||||
| 4,5 | 4,7 | |||||||||||||||||||||||
| 3,0 | 3,12 | |||||||||||||||||||||||
| 4,1 | 4,0 | 4,4 | 4,6 | 4,8 | 4,12 | 4,11 | ||||||||||||||||||
| 5,2 | 5,0 | 5,5 | 5,6 | 5,7 | 5,12 | 5,10 | ||||||||||||||||||
| 6,3 | 6,2 | 6,1 | 6,0 | 6,4 | 6,5 | 6,6 | 6,7 | 6,8 | 6,12 | 6,11 | 6,10 | 6,9 | ||||||||||||
| 7,2 | 7,0 | 7,5 | 7,6 | 7,7 | 7,12 | 7,10 | ||||||||||||||||||
| 8,1 | 8,0 | 8,4 | 8,6 | 8,8 | 8,12 | 8,11 | ||||||||||||||||||
| 9,0 | 9,12 | |||||||||||||||||||||||
| 8,5 | 8,7 | |||||||||||||||||||||||
| 7,4 | 7,8 | |||||||||||||||||||||||
| 9,3 | 9,9 | |||||||||||||||||||||||
| 10,0 | 10,2 | 10,1 | 10,11 | 10,10 | 10,12 | |||||||||||||||||||
| 11,0 | 11,1 | 11,2 | 11,10 | 11,11 | 11,12 | |||||||||||||||||||
| 12,0 | 12,1 | 12,2 | 12,3 | 12,4 | 12,5 | 12,6 | 12,7 | 12,8 | 12,9 | 12,10 | 12,11 | 12,12 | ||||||||||||
| 11,4 | 11,6 | 11,8 | ||||||||||||||||||||||
| 10,5 | 10,6 | 11,8 | ||||||||||||||||||||||
| 9,6 |
![]()
Iso-like
Generating magic square is quadrant magic and order 8n + 1 or 8n + 3
Resulting star is of pattern 8B with 12 lines of n numbers summing correctly.
Magic square is plusmagic (required to form main diagonals)
If magic square is diamagic, only 10 lines of n numbers sum correctly and it is called incomplete
No numbers are duplicated but not all numbers are used.Isomorphic
Generating magic square is order-4, any type, or order-5 plusmagic only
Order-4; the star will be type 8B normal with 8 lines of 4 numbers (mapping will vary)
Order-5; the star will be type 8B with 12 lines of 5 numbers
In both cases, all numbers are used with no duplicatesPan-magic
Generating magic square is pandiagonal odd order greater then five
Resulting star is of pattern 8B with 10 or 12 lines of m numbers summing correctly.
Not all numbers are used and there will be either 4 or 8 numbers duplicated
A variation is the butterfly, a 12 pointed star with 20 lines of 9 numbers summing correctly
Note that pan-magic stars do not require that the generating square be quadrant magic, only pandiagonal.
Some regular (not pandiagonal) magic squares of order-5 are plusmagic and can thus form
Isomorphic magic stars.
Are there plusmagic regular magic squares of other
orders?
Are all orders 4n + 1 that are plusmagic, also
crossmagic? No.
Note that the crossmagic array is of no use in the construction of pan-magic stars because
one arm of the cross always falls on the main diagonal of the square.
Order-5 plusmagic squares may be considered to also be diammagic with sides of length 2.
(Order-9 diammagic arrays have length 3, and order-13 have length 4.)
There seem to be no pandiagonal order-9 plusmagic squares.
Are there any regular order-9 magic squares that are
plusmagic ?
Are there any plusmagic squares of any order 8m+1? Yes.
| Addendum. June 18,1999. Other orders 4n + 1 may have either crossmagic or plusmagic or possibly both in the same square. There are order-17 plusmagic squares which makes the construction of order-17 complete isolike magic stars possible. |
![]()
Summary
Isolike magic stars are all of pattern order-8B. The pattern consists
of superimposed squares, one of which is rotated 45 degrees. Each of these squares is
bisected in both directions by additional lines.
Construct the normal square from the original top and bottom row, and the left and right
column of the magic square. The four lines of the 45 degree rotated square is constructed
from the diammagic or plusmagic array in each quadrant of the magic square. Of course the
patterns used for a particular star must all be crossmagic or all diammagic.
The center vertical and horizontal lines are from the corresponding lines of the magic
square.
The two internal diagonal lines are also form the main diagonals of the magic square.
An incomplete isolike magic star results if the two main diagonals
cannot be made magic without the use of duplicate numbers, and only 10 lines sum
correctly.
The problem arises when more then one number in the plusmagic or diammagic array is on the
main diagonal of the magic square. The magic star then will require duplicate numbers in
order for the main diagonals to be magic. This happens with the diammagic square of order
8n + 1. It also happens with all orders of crossmagic and sringmagic squares.
The reason lringmagic squares cannot produce isolike magic stars, is because more then 1
number of the array is common to the adjacent array.
Order-5 pandiagonal (and some regular) magic squares can form fully
isomorphic magic stars.
Orders 8m-3 (such as 13, 21, etc) can form complete isolike magic
stars.
Orders 4m-1 magic squares cannot form isolike magic stars because
there can be no quadrant magic square for these orders.
Orders 8m+1 (such as 9, 17, etc) diammagic squares cannot form
complete pan-magic stars because some of the numbers on the side of the diamond falls on
the main diagonal of the square, which would require duplicate numbers in order to form
the diagonals. If, however, there are plusmagic squares of these orders, complete isolike
magic stars could be constructed from them. (See addendum above.)
Isolike magic stars cannot be constructed from the other three types of quadrant magic
squares. crossmagic and sringmagic squares have more then one number of the array
falling on the main diagonal. Lringmagic squares have more then one number in common with
an adjacent array.
Note that pan-magic stars can be constructed from pandiagonal magic squares that are not plusmagic or diammagic. This was de Winkel's original intention. However, it is impossible to compose 12 line pan-magic stars of this type without using duplicate numbers. This was explained when describing the order-7 situation.
See my page on Quadrant Magic Squares.
Finally, my thanks again to Aale de Winkel for the basic idea, and all the help I received in developing isolike magic stars.
A final Note:
A fully isomorphic magic star may be constructed from an order 4 magic square.
It is a pure type 8A star containing 8 lines of 4 numbers. See an example on my Unusual Magic Squares page.
![]()
Please send me Feedback about my Web site!
Harvey Heinz harveyheinz@shaw.ca
This page last updated
April 04, 2007
Copyright © 1999, 2000 by Harvey D. Heinz