 |
 |
 |
 |
 |
I hope you enjoy these examples of a variety of magic squares.
This section of my site consists mostly of examples, with a minimum of explanation and
theory.
Refer to the other two sections for Magic Stars and Number Patterns.
This site should be of interest to middle and high school students and teachers, and
anyone interested in recreational mathematics.
![]()
Order-3 |
Order-4 |
Order-5 |
Magic Squares are a form of number pattern that has been around for thousands of years.
For a pure or normal magic square, all rows, columns, and the two
main diagonals must sum to the same value and the numbers used must be consecutive from 1
to n2, where n is the order of the square.
Many variations exist that contain numerous other features.
I show on these pages samples of the large variety of magic squares. My descussions will be limited to brief comments on the individual illustrations. Perhaps in the future, I will add more in depth information in the way of history, theory, construction methods, etc.
Acknowledgments: As with all the mateial on this site, most of these illustrations are original with myself or I consider them in the public domain (i.e. I have multiple sources for the illustration). Many of the more unusual figures are one of a kind and I so acknowledge the author with thanks for permission to use them.
Set of Orders 3, 4, and 5 |
Together use the numbers 1 to 50. |
Orders 3, 5, 7, 9 Inlaid |
This and next magic square by John Hendricks. Order 3 is diamond, 7 & 9 frames. |
Order-20 with 4 Inlays |
This was assembled from boilerplate sets. Ten different magic squares (in this case). |
Four plus five equals nine |
An order-4 & an order-5 combine to make an order-9 magic square. |
Order-18 based on 1/19 |
This is a simple pure magic square based on the cyclic number 19. |
Following |
are some of the related pages on this site |
Anti-magic Squares |
Examples of different orders of anti-magic and heterosquares. |
Compact magic squares |
Some order-8 pandiagonal magic squares that have the compact feature. |
FranklinSquares |
The 3 traditional magic figures plus 3 new, including the recently discovered 16x16. |
How many groups = 65? |
in this Order-5 Pandiagonal, Associative, Complete & Self-similar Magic Square? |
John Hendricks - Cubes |
Some of his large variety of inlaid magic squares, cubes, and hypercubes. |
Knight tours |
Tracing a path with chess knight moves such that the numbered steps form a magic square. |
Magic Square models |
Photos of models of 3_D magic star, order-3 magic cube, etc. |
Material from REC |
Some magic squares from Recreational & Educational Computing newsletter. |
More Magic Squares |
A continuation of this page. |
More Magic squares-2 |
A continuation of the above page. |
Most-perfect magic squares |
A subset of pandiagonal magic squares that possesses additional features. |
Most-perfect Bent diagonal |
Bent-diagonal (Franklin type) magic squares with the added feature that they are most-perfect pandiagonal. |
Multimagic Squares |
The new Order-12 Trimagic, new tetra and pentamagic squares, new bimagic cube. |
Order-3 type-2 magic sqrs. |
Turns out the order-3 comes in two varieties. i.e. two different layouts. |
Order-4 Magic Squares |
Dudeney group patterns. Groups I, II, III, XI and XII in magic square format.. All 880 magic squares in index order, in a tabular list format. |
Perimeter magic polygons |
Perimeter magic triangles and other polygons. Plus two subsidiary pages. |
Prime Magic Squares |
A variety of magic squares constructed with prime numbers. |
Quadrant Magic Squares |
A magic pattern appears in each quadrant. There are many such patterns. |
Self-similar magic squares |
Magic squares that produce copies of themselves. |
The order-5 pandiagonals |
Lists 36 essentially different squares. Each of these has 100 variations. |
Transformations & Patterns |
40+ methods to transform an order-4 magic square. Also lists and groups. |
Unusual magic squares |
A variety of magic squares. A pandiagonal magic square generator. |
Trump - Ultra-magic squares |
Some unusual magic squares designed by Walter Trump |
Magic Square Update |
3 new types of m.s., 1040 order-4 ?, How Many ?, Postage stamp |
Site Map |
Titles and relationship of all pages on this site (and related sites below) with direct links. |
Following |
are related sites (by this author) on other servers |
Magic cubes |
About 45 pages dealing with these 3-D hypercubes |
Magic tesseracts |
11 pages dealing with these 4-D hypercubes (New! November 2007) |
Links to similar web sites |
Other Magic Square pages or Recreational Mathematics sites (by other authors). |
![]()
|
|
|
Three simple magic squares together use the numbers from 1 to 50. None of the three is a pure magic square because none uses consecutive numbers starting at 1. However, the order 5 square is pandiagonal. S3 = 69, S4 = 102, S5 = 132
![]()
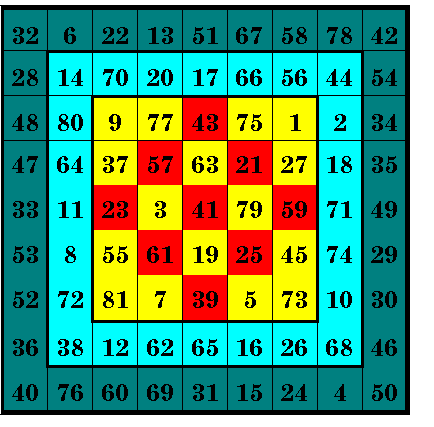
John R. Hendrick's inlaid magic squares
An order-9 magic square with three inlaid magic squares of Orders 3, 5, and 7. The
order-3 is rotated 45 degrees and is referred to as a diamond inlay. Note that the smaller
and larger numbers are mixed throughout the square, not in the outside
border as they would be with a bordered magic square.
These outside rings are called expansion bands to diferentiate them from the borders (of a
bordered or concentric magic square), which have 2n+2 low and high numbers in the
border .
S3 = 123, S5 = 205, S7 = 287, S9 = 369.
Numbers used are 1 to 81, so Order-9 is a pure magic square.
![]()
400 |
9 |
16 |
13 |
18 |
2 |
7 |
4 |
10 |
6 |
395 |
391 |
397 |
394 |
399 |
383 |
388 |
385 |
12 |
381 |
161 |
232 |
225 |
228 |
223 |
239 |
234 |
237 |
231 |
235 |
166 |
170 |
164 |
167 |
162 |
178 |
173 |
176 |
229 |
180 |
301 |
92 |
219 |
83 |
57 |
379 |
323 |
45 |
371 |
95 |
315 |
357 |
199 |
23 |
125 |
74 |
311 |
248 |
312 |
81 |
241 |
152 |
263 |
214 |
157 |
268 |
145 |
271 |
159 |
155 |
255 |
34 |
131 |
68 |
317 |
259 |
343 |
185 |
252 |
141 |
341 |
52 |
368 |
88 |
205 |
337 |
91 |
334 |
54 |
55 |
355 |
79 |
303 |
245 |
354 |
191 |
28 |
137 |
352 |
41 |
21 |
372 |
59 |
274 |
97 |
211 |
325 |
148 |
363 |
375 |
35 |
251 |
348 |
197 |
39 |
123 |
65 |
314 |
32 |
361 |
121 |
272 |
143 |
328 |
331 |
85 |
217 |
94 |
279 |
275 |
135 |
183 |
25 |
134 |
71 |
308 |
257 |
359 |
132 |
261 |
61 |
332 |
374 |
151 |
265 |
154 |
277 |
208 |
48 |
335 |
75 |
128 |
77 |
319 |
243 |
345 |
194 |
31 |
72 |
321 |
181 |
212 |
51 |
339 |
365 |
43 |
99 |
377 |
203 |
215 |
195 |
305 |
254 |
351 |
188 |
37 |
139 |
63 |
192 |
201 |
101 |
292 |
285 |
288 | 283 |
299 |
294 |
297 |
291 |
295 |
115 |
111 |
117 |
114 |
119 |
103 |
108 |
105 |
112 |
281 |
300 |
109 |
296 |
293 |
298 |
282 |
287 |
284 |
290 |
286 |
106 |
110 |
104 |
107 |
102 |
118 |
113 |
116 |
289 |
120 |
220 |
189 |
202 |
98 |
44 |
362 |
338 |
56 |
370 |
206 |
186 |
182 |
318 |
344 |
22 |
78 |
356 |
30 |
209 |
200 |
340 |
69 |
278 |
204 |
270 |
336 |
87 |
153 |
142 |
326 |
66 |
138 |
316 |
244 |
130 |
184 |
76 |
242 |
329 |
80 |
280 |
129 |
373 |
327 |
93 |
144 |
210 |
276 |
47 |
266 |
126 |
33 |
73 |
253 |
67 |
247 |
310 |
347 |
269 |
140 |
380 |
29 |
42 |
150 |
216 |
267 |
333 |
84 |
378 |
366 |
26 |
342 |
187 |
124 |
190 |
256 |
193 |
38 |
369 |
40 |
60 |
349 |
158 |
273 |
324 |
90 |
156 |
207 |
262 |
46 |
346 |
258 |
70 |
133 |
313 |
127 |
307 |
122 |
49 |
360 |
160 |
249 |
367 |
96 |
147 |
213 |
264 |
330 |
53 |
146 |
246 |
27 |
304 |
196 |
250 |
136 |
64 |
353 |
149 |
260 |
100 |
309 |
50 |
322 |
376 |
58 |
82 |
364 |
218 |
86 |
306 |
350 |
62 |
36 |
358 |
302 |
24 |
198 |
89 |
320 |
221 |
172 |
236 |
233 |
238 |
222 |
227 |
224 |
230 |
226 |
175 |
171 |
177 |
174 |
179 |
163 |
168 |
165 |
169 |
240 |
20 |
389 |
5 |
8 |
3 |
19 |
14 |
17 |
11 |
15 |
386 |
390 |
384 |
387 |
382 |
398 |
393 |
396 |
392 |
1 |
J.R.Hendricks, Magic square course (self-published) pp290-294
I assembled this from a boilerplate design by John Hendricks. He provides the frame,
and four of each of the order-7 inlays,
one for each quadrant. It is then simply a matter of deciding which type of inlay to put
in each quadrant.
The order-7 (upper right corner) is a pandiagonal so may be altered by shifting rows or
columns.
The order-5 (lower left quadrant) is also a pandiagonal.
The order-20, because it contains the consecutive numbers from 1 to 400, is a pure magic
square
Magic sums are: U.L. 1477, 1055, 633; -- U.R. 1337; -- L.L. 1470, 1050; -- L. R.
1330, 950, 570
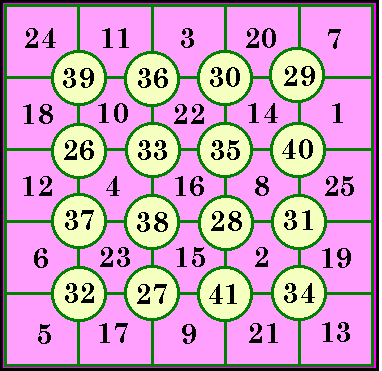
Numbers 1 to 25 arranged as an order-5 pandiagonal pure magic square.
Numbers 26 to 41 arranged as an embedded order-4 pandiagonal magic square.
Together, they make an order-9 magic square. Any one of the rows and any one of the columns of the order-4 is counted twice.
S4 = 134, S5 = 65, S9 = 199
If we use the series from 70 to 110 instead of 1 to 41, the magic constant of both order-4 and order-5 is 410 !
As far as I can determine, this type of magic square originated with Kenneth Kelsey of Great Britain.
![]()
The number 19 is a cyclic number with a period of 18 before the digits start
to repeat.
The full term decimal expansion of the prime number 19 when multiplied by the values 1
to 18, may be arranged in a simple magic square of order-18, if the decimal point is
ignored. All 18 rows, columns and the two main diagonals sum to the same value. S = 81. Of
course this is not a pure magic square because a consecutive series of numbers
from 1 to n is not used.
Point of interest: 81 is also a cyclic number (of period 9). 1/81 = .0123456790123456 ...
. Only the 8 is missing. Too bad!
1/19 = |
.0 |
5 |
2 |
6 |
3 |
1 |
5 |
7 |
8 |
9 |
4 |
7 |
3 |
6 |
8 |
4 |
2 |
1 |
2/19 = |
.1 |
0 |
5 |
2 |
6 |
3 |
1 |
5 |
7 |
8 |
9 |
4 |
7 |
3 |
6 |
8 |
4 |
2 |
3/19 = |
.1 |
5 |
7 |
8 |
9 |
4 |
7 |
3 |
6 |
8 |
4 |
2 |
1 |
0 |
5 |
2 |
6 |
3 |
4/19 = |
.2 |
1 |
0 |
5 |
2 |
6 |
3 |
1 |
5 |
7 |
8 |
9 |
4 |
7 |
3 |
6 |
8 |
4 |
5/19 = |
.2 |
6 |
3 |
1 |
5 |
7 |
8 |
9 |
4 |
7 |
3 |
6 |
8 |
4 |
2 |
1 |
0 |
5 |
6/19 = |
.3 |
1 |
5 |
7 |
8 |
9 |
4 |
7 |
3 |
6 |
8 |
4 |
2 |
1 |
0 |
5 |
2 |
6 |
7/19 = |
.3 |
6 |
8 |
4 |
2 |
1 |
0 |
5 |
2 |
6 |
3 |
1 |
5 |
7 |
8 |
9 |
4 |
7 |
8/19 = |
.4 |
2 |
1 |
0 |
5 |
2 |
6 |
3 |
1 |
5 |
7 |
8 |
9 |
4 |
7 |
3 |
6 |
8 |
9/19 = |
.4 |
7 |
3 |
6 |
8 |
4 |
2 |
1 |
0 |
5 |
2 |
6 |
3 |
1 |
5 |
7 |
8 |
9 |
10/19= |
.5 |
2 |
6 |
3 |
1 |
5 |
7 |
8 |
9 |
4 |
7 |
3 |
6 |
8 |
4 |
2 |
1 |
0 |
11/19= |
.5 |
7 |
8 |
9 |
4 |
7 |
3 |
6 |
8 |
4 |
2 |
1 |
0 |
5 |
2 |
6 |
3 |
1 |
12/19= |
.6 |
3 |
1 |
5 |
7 |
8 |
9 |
4 |
7 |
3 |
6 |
8 |
4 |
2 |
1 |
0 |
5 |
2 |
13/19= |
.6 |
8 |
4 |
2 |
1 |
0 |
5 |
2 |
6 |
3 |
1 |
5 |
7 |
8 |
9 |
4 |
7 |
3 |
14/19= |
.7 |
3 |
6 |
8 |
4 |
2 |
1 |
0 |
5 |
2 |
6 |
3 |
1 |
5 |
7 |
8 |
9 |
4 |
15/19= |
.7 |
8 |
9 |
4 |
7 |
3 |
6 |
8 |
4 |
2 |
1 |
0 |
5 |
2 |
6 |
3 |
1 |
5 |
16/19= |
.8 |
4 |
2 |
1 |
0 |
5 |
2 |
6 |
3 |
1 |
5 |
7 |
8 |
9 |
4 |
7 |
3 |
6 |
17/19= |
.8 |
9 |
4 |
7 |
3 |
6 |
8 |
4 |
2 |
1 |
0 |
5 |
2 |
6 |
3 |
1 |
5 |
7 |
18/19= |
.9 |
4 |
7 |
3 |
6 |
8 |
4 |
2 |
1 |
0 |
5 |
2 |
6 |
3 |
1 |
5 |
7 |
8 |
This magic square was designed by Harry A. Sayles and published in the Monist before
1916.
W. S. Andrews, Magic Squares and Cubes, Dover Publ., 1917, p.176
The next cyclic number (in base 10) that is capable of forming a magic square in this
fashion, is n/383.
In an e-mail dated July 20/01, Simon Whitechapel pointed out that many such magic squares
may be formed using full period cyclic numbers in other bases.
Below we show that the numbers n/19 can be multiplied simply by shifting left. Obviously, each row and column add to the same value (a property of all such lists).
1/19 = .0 5 2 6 3 1 5 7 8 9 4 7 3 6 8 4 2 1 10/19 = .5 2 6 3 1 5 7 8 9 4 7 3 6 8 4 2 1 0 5/19 = .2 6 3 1 5 7 8 9 4 7 3 6 8 4 2 1 0 5 12/19 = .6 3 1 5 7 8 9 4 7 3 6 8 4 2 1 0 5 2 6/19 = .3 1 5 7 8 9 4 7 3 6 8 4 2 1 0 5 2 6 3/19 = .1 5 7 8 9 4 7 3 6 8 4 2 1 0 5 2 6 3 11/19 = .5 7 8 9 4 7 3 6 8 4 2 1 0 5 2 6 3 1 15/19 = .7 8 9 4 7 3 6 8 4 2 1 0 5 2 6 3 1 5 17/19 = .8 9 4 7 3 6 8 4 2 1 0 5 2 6 3 1 5 7 18/19 = .9 4 7 3 6 8 4 2 1 0 5 2 6 3 1 5 7 8 9/19 = 4 7 3 6 8 4 2 1 0 5 2 6 3 1 5 7 8 9 14/19 = .7 3 6 8 4 2 1 0 5 2 6 3 1 5 7 8 9 4 7/19 = .3 6 8 4 2 1 0 5 2 6 3 1 5 7 8 9 4 7 13/19 = .6 8 4 2 1 0 5 2 6 3 1 5 7 8 9 4 7 3 16/19 = .8 4 2 1 0 5 2 6 3 1 5 7 8 9 4 7 3 6 8/19 = .4 2 1 0 5 2 6 3 1 5 7 8 9 4 7 3 6 8 4/19 = .2 1 0 5 2 6 3 1 5 7 8 9 4 7 3 6 8 4 2/19 = .1 0 5 2 6 3 1 5 7 8 9 4 7 3 6 8 4 2
Use the links at the top of this page to access other magic square pages on this site.
Thanks again for the visit and I hope to see you again soon.

![]() Please send me Feedback about my Web site!
Please send me Feedback about my Web site!![]()

![]()
Harvey Heinz harveyheinz@shaw.ca
This page last updated
October 05, 2009
Copyright © 1998,1999, 2000 by Harvey D. Heinz