 |
 |
 |
 |
 |
![]()
Introduction |
A bit about Ben Franklin. Then what this page is about and a credit to Paul C. Pasles. |
Franklin’s Order-8 |
This well-known square was mentioned in a letter about 1752 and first published in 1769. |
The well known 16x16 |
This well-known square was mentioned in a letter about 1752 and first published in 1767. |
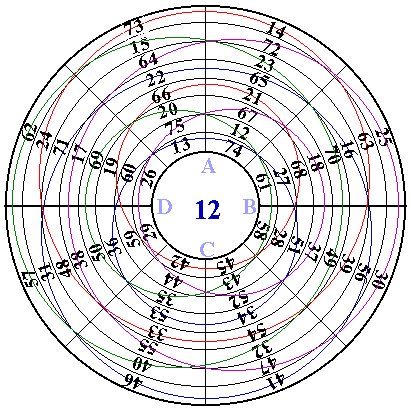
Franklin’s magic circle |
This circle was also published in Franklin's lifetime and is fairly well known. |
Franklin’s Other squares |
The newly discovered order-4, order-6, and preliminary mention of the remarkable order-16. |
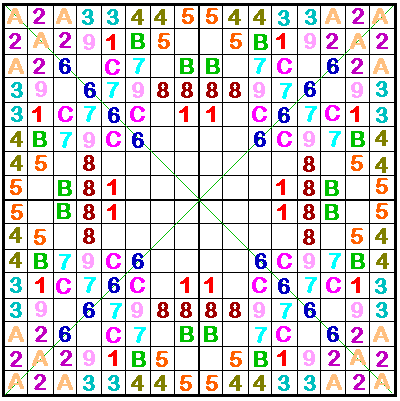
Franklin's new order-16 |
A variation of the newly discovered square and a comparison with the well-known one. |
Feature Comparison |
Feature comparison table between Franklin’s old and new order-16 squares. |
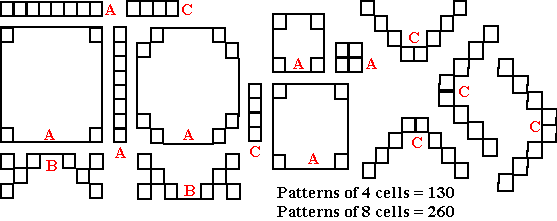
Small patterns |
An arbitrary selection of 12 patterns of 16 cells found in the order-16 squares. |
Large patterns |
An arbitrary selection of 12 patterns of 16 cells found in the order-16 squares. |
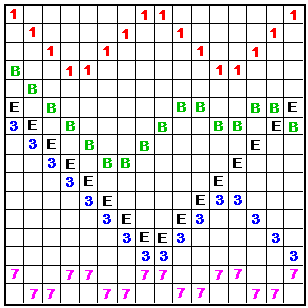
Bent diagonal patterns |
An arbitrary selection of 16 zig-zag patterns of 16 cells found in the order-16 squares. |
Knight move diagonals |
Diagrammed are 4 knight move diagonal patterns found in both squares. |
Conclusion |
A summery of the information contained on this page. |
Order-8 Franklin Squares Counted! |
There are 368,640 order-8 bent-diagonal pandiagonal magic squares. Peter Loly 2006. |
Benjamin Franklin (1706-1790), the early American scientist, statesman and author, is known as the creator of bent-diagonal magic squares. (Actually these squares are not magic in the accepted definition because the two main diagonals do not sum correctly.)
In his lifetime he published an order-8, an order-16 and a magic circle. The order-16 and the magic circle were first published in Ferguson’s Tables and Tracts Relative to Several Arts and Sciences (London,1767). In the next few years, all three were published in various works and personal letters.
These three have been published many times since and will be reproduced here.
It has
recently been revealed in a superbly researched and written paper by Paul C. Pasles that,
in fact, Franklin composed four other squares; an order-4, an order-6, another
order-8 and another order-16. |
The orders 4, 6 and 8 will be reproduced below. A variation of the order-16 (by moving four columns from the left to the right sides) will also be shown, as well as a feature comparison of Franklin’s two squares and my modified one.
The paper mentioned above is Paul C. Pasles, The Lost Squares of Dr. Franklin: Ben Franklin’s Missing Squares and the Secret of the Magic Circle, The American Mathematical Monthly, 108:6, June-July, 2001, pp 489-511. It includes 49 citations.
I extend my thanks to Paul C. Pasles, for bringing this exciting news to the attention of recreational math buffs. Much of the information on these pages was derived from his paper. See also, his Web page at http://www.pasles.org/Franklin.html .
Donald Morris has an attractive new site (February
2006) on Franklin Squares. He explains what he thinks is Franklins method of
construction.
He also explains his own method and shows some excellent examples.
This excellent site is at
http://www.bestfranklinsquares.com/franklinsquares.html Oops! gone now?
![]()
|
This square has Franklin's trademark, the bent-diagonals. However, because
the main diagonals do not sum correctly (one totals 260 - 32 & the other 260 + 32), it
is not a true magic square. The Franklin order-8 and order-16 squares have the feature that you can move a group of 4 rows or 4 columns to the opposite side and all features will be retained. This magic square was constructed by Benjamin Franklin and first mentioned in a letter to Peter Collinson of England about 1752. It was subsequently published in Franklin's Experiments and Observations in Electricity (London, 1569) It has many interesting properties as illustrated by the following cell patterns. |
 |
|
![]()
This square was published during Franklin’s lifetime (in 1767),
and has been published many times since.
It contains most of the same patterns that appear in his order-8 square, plus many more.
It contains the bent diagonals which are a trademark of his squares. However, like his
order-8, it is not considered a true magic square because the main diagonals do not sum
correctly (one sums 128 too low, the other 128 too high).
This square will be compared later with the newly discovered square when we look at the many embedded patterns.
NOTE: This square can be made magic simply by rotating the top right quadrant clockwise and the bottom right quadrant counterclockwise. However, this results in the bent diagonal and some other features being destroyed. This same trick may be used to make the order-8's magic.
| 200 | 217 | 232 | 249 | 8 | 25 | 40 | 57 | 72 | 89 | 104 | 121 | 136 | 153 | 168 | 185 |
| 58 | 39 | 26 | 7 | 250 | 231 | 218 | 199 | 186 | 167 | 154 | 135 | 122 | 103 | 90 | 71 |
| 198 | 219 | 230 | 251 | 6 | 27 | 38 | 59 | 70 | 91 | 102 | 123 | 134 | 155 | 166 | 187 |
| 60 | 37 | 28 | 5 | 252 | 229 | 220 | 197 | 188 | 165 | 156 | 133 | 124 | 101 | 92 | 69 |
| 201 | 216 | 233 | 248 | 9 | 24 | 41 | 56 | 73 | 88 | 105 | 120 | 137 | 152 | 169 | 184 |
| 55 | 42 | 23 | 10 | 247 | 234 | 215 | 202 | 183 | 170 | 151 | 138 | 119 | 106 | 87 | 74 |
| 203 | 214 | 235 | 246 | 11 | 22 | 43 | 54 | 75 | 86 | 107 | 118 | 139 | 150 | 171 | 182 |
| 53 | 44 | 21 | 12 | 245 | 236 | 213 | 204 | 181 | 172 | 149 | 140 | 117 | 108 | 85 | 76 |
| 205 | 212 | 237 | 244 | 13 | 20 | 45 | 52 | 77 | 84 | 109 | 116 | 141 | 148 | 173 | 180 |
| 51 | 46 | 19 | 14 | 243 | 238 | 211 | 206 | 179 | 174 | 147 | 142 | 115 | 110 | 83 | 78 |
| 207 | 210 | 239 | 242 | 15 | 18 | 47 | 50 | 79 | 82 | 111 | 114 | 143 | 146 | 175 | 178 |
| 49 | 48 | 17 | 16 | 241 | 240 | 209 | 208 | 177 | 176 | 145 | 144 | 113 | 112 | 81 | 80 |
| 196 | 221 | 228 | 253 | 4 | 29 | 36 | 61 | 68 | 93 | 100 | 125 | 132 | 157 | 164 | 189 |
| 62 | 35 | 30 | 3 | 254 | 227 | 222 | 195 | 190 | 163 | 158 | 131 | 126 | 99 | 94 | 67 |
| 194 | 223 | 226 | 255 | 2 | 31 | 34 | 63 | 66 | 95 | 98 | 127 | 130 | 159 | 162 | 191 |
| 64 | 33 | 32 | 1 | 256 | 225 | 224 | 193 | 192 | 161 | 160 | 129 | 128 | 97 | 96 | 65 |
![]()
Franklin mentioned this(?) magic circle in a letter to Collinson about 1752, although the circle itself may not have been made public until 1767, as mentioned in the introduction.
 |
This square was found on a piece of scrap paper with Franklin’s notes, and had no accompanying explanation. Pasles believes it formed the basis for the design of the above magic circle. He provides a plausible algorithm in his paper for its use in this regard.
This order-8 has been previously published only once, as a footnote to the Papers of Benjamin Franklin, 1961. It has most of the same characteristics as the 8x8 shown above (the 2 'B' patterns are not valid). |
The reason for this magic circle starting at 12 and having a constant 12 in the center
is believed to be so the sum would be 360, signifying the number of degrees in a circle.
This diagram is a modern rendering of Franklin's design. He apparently had 20 eccentric
circles in his version. I have limited these to 8 in the interest of improved readability.
Order-4
This square is semi-pandiagonal associative magic, but is rather a
disappointment because it contains nothing new. In fact, it was discovered by Bernard
Frénicle de Bessy, probably around 1665, and was published with his list of all 880
order-4 magic squares in 1676. It is one of the 48 semi-pandiagonal, associative magic
squares of Group III, so does not even have the bent-diagonal feature. Franklin was
probably unaware of the published list of order-4 squares, and was obviously unaware that
there did exist 48 fully magic order-4 bent-diagonal magic squares (group II).
See my Order-4 page for more information on these squares.
|
|
Order-6
The main diagonals are bent, i.e 2+32+8+33+5+31=111 so this square is not a true magic square. However, note that the two bottom quadrants are magic order-3 squares. By simply swapping the two halves of the second row from the top, these top two quadrants also become order-3 magic. If this 6 x 6 square is split into two horizontal 3 x 6 rectangles, each rectangle is associated. That is, diametrically opposed numbers such as 2 + 35, 32 + 5, 27+10, etc. sum to 37.
Neither the 4 x 4 or the 6 x 6 square had been published previous to Pasles paper.
Order-8
A relatively unknown order-8 was found on a scrap of paper with Franklin’s notes. Because it may have figured in the construction of his magic circle, it is displayed in that section.
Order-16
I have chosen not to show this remarkable square, which has many
features not found in his well known square.
Instead I have shown my variation, which was constructed by simply moving 4 columns from
the left to the right side.
Continuous nature of Franklin squares
Franklin squares are not fully magic (except for the newly discovered
order-16. However, they are continuous in the sense that all patterns that run over an
edge continue on the opposite edge as pandiagonal magic squares do.
The 8x8 and 16x16 squares may be transformed to a different bent-diagonal square by moving
two rows or columns to the opposite edge with many features being retained. However,
because some patterns of these squares start only on every forth row and/or column, 4 rows
or columns must be moved to retain all the features of the square.
Franklin’s recently discovered square, unlike the well-known 16
x 16, is fully pandiagonal magic. As mentioned previously, all his
squares are continuous because all patterns running off of an edge continue on the
opposite edge. However, this square differs because it has a pattern of n adjacent numbers
in a straight diagonal. The other squares have only diagonals of n/2 (the reason they are
not true magic squares).
Of course, it still has the bent-diagonal feature as well!
| 14 | 253 | 4 | 243 | 12 | 251 | 6 | 245 | 10 | 249 | 8 | 247 | 16 | 255 | 2 | 241 |
| 3 | 244 | 13 | 254 | 5 | 246 | 11 | 252 | 7 | 248 | 9 | 250 | 1 | 242 | 15 | 256 |
| 238 | 29 | 228 | 19 | 236 | 27 | 230 | 21 | 234 | 25 | 232 | 23 | 240 | 31 | 226 | 17 |
| 227 | 20 | 237 | 30 | 229 | 22 | 235 | 28 | 231 | 24 | 233 | 26 | 225 | 18 | 239 | 32 |
| 221 | 46 | 211 | 36 | 219 | 44 | 213 | 38 | 217 | 42 | 215 | 40 | 223 | 48 | 209 | 34 |
| 212 | 35 | 222 | 45 | 214 | 37 | 220 | 43 | 216 | 39 | 218 | 41 | 210 | 33 | 224 | 47 |
| 61 | 206 | 51 | 196 | 59 | 204 | 53 | 198 | 57 | 202 | 55 | 200 | 63 | 208 | 49 | 194 |
| 52 | 195 | 62 | 205 | 54 | 197 | 60 | 203 | 56 | 199 | 58 | 201 | 50 | 193 | 64 | 207 |
| 78 | 189 | 68 | 179 | 76 | 187 | 70 | 181 | 74 | 185 | 72 | 183 | 80 | 191 | 66 | 177 |
| 67 | 180 | 77 | 190 | 69 | 182 | 75 | 188 | 71 | 184 | 73 | 186 | 65 | 178 | 79 | 192 |
| 174 | 93 | 164 | 83 | 172 | 91 | 166 | 85 | 170 | 89 | 168 | 87 | 176 | 95 | 162 | 81 |
| 163 | 84 | 173 | 94 | 165 | 86 | 171 | 92 | 167 | 88 | 169 | 90 | 161 | 82 | 175 | 96 |
| 157 | 110 | 147 | 100 | 155 | 108 | 149 | 102 | 153 | 106 | 151 | 104 | 159 | 112 | 145 | 98 |
| 148 | 99 | 158 | 109 | 150 | 101 | 156 | 107 | 152 | 103 | 154 | 105 | 146 | 97 | 160 | 111 |
| 125 | 142 | 115 | 132 | 123 | 140 | 117 | 134 | 121 | 138 | 119 | 136 | 127 | 144 | 113 | 130 |
| 116 | 131 | 126 | 141 | 118 | 133 | 124 | 139 | 120 | 135 | 122 | 137 | 114 | 129 | 128 | 143 |
This variation of Franklin’s newly discovered 16 x 16 magic square was constructed by simply moving four columns from the left side of his square to the right side. Every pattern tested on this square was also tested on an exact copy of his square (as presented in Pasles paper), to confirm that the features are identical.
![]()
The square illustrated above has the exact same features as Franklin’s new square.
I will present a condensed comparison list, then sub-sections showing the small patterns, large patterns, bent-diagonal and knight-move patterns tested.
The word ‘All’ in the following table indicates that the pattern sums correctly if started in ANY of the 256 cells of the square!
Small patterns: 16 cells that all fit within one quadrant.
Large patterns: 4 groups of 4 cells spread over all 4 quadrants.
I arbitrarily defined the starting cell of the pattern to be the top cell in the leftmost column of the pattern.
# |
Pattern Description |
Original 16 x 16 |
New 16 x 16 (& modified one) |
1 |
4 x 4 blocks = S |
All |
All |
2 |
2 x 2 blocks = S/4 |
All |
All |
3 |
Leading 4 cell diagonals = S/4 |
None |
Start on Any ODD column & rows 3, 7, 11, 15 |
4 |
Right 4 cell diagonals = S/4 |
None |
Start on Any ODD column & rows 2, 6, 10, 14 |
5 |
Leading 8 cell diagonals = S/2 |
None |
Start on ANY ODD row & col. |
6 |
Right 8 cell diagonals = S/2 |
None |
Start on ANY even row & ODD column |
7 |
Leading 16 cell diagonals = S |
None |
All - This (and next) is what makes this square magic (and pandiagonal)! |
8 |
Right 16 cell diagonals = S |
None |
All |
9 |
Rows of 2 cells = S/8 |
All starting with col. 4 & 12 |
All starting with columns 2, 6, 10, 14 |
10 |
Columns of 2 cells = S/8 |
None ! |
None !!! |
11 |
Any row of 4 cells = S/4 |
All starting on columns 3 & 11 |
All starting on col. 1, 5, 9, 13 |
12 |
Any column of 4 cells = S/4 |
All starting on rows 3 & 11 |
NO columns of 4 cells sum to S/4 !!!
|
13 |
Any row of 8 cells = S/2 |
All starting on columns 1 & 9 |
All starting on col. 1, 5, 9, 13 |
14 |
Any column of 8 cells = S/2 |
All starting on rows 1 & 9 |
All starting on rows 1, 5, 9, 13 |
15 |
Is this square magic? |
No |
Yes – pandiagonal magic! |
16 |
Embedded 8 x 8 magic squares |
The one in each quadrant is semi-magic |
All starting on rows & columns 1, 5 , 9, 13 are pandiagonal magic. |
17 |
Corners of 4 x 4 |
All |
All |
18 |
Corners of 6 x 6 |
All |
All |
19 |
Corners of 8 x 8 |
All |
All |
20 |
Corners of 10 x 10 |
All |
All |
21 |
Corners of 12 x 12 |
All |
All |
22 |
Corners of 14 x 14 |
All |
All |
23 |
Corners of 16 x 16 |
All |
All |
24 |
Small Pattern 1 – diamond |
All |
All |
25 |
SP2 – box |
All |
All |
26 |
SP3 – large x |
All |
All |
27 |
SP4 – small diamond |
All |
All |
28 |
SP5 to 8, 10-12 |
All |
All |
35 |
Pattern 9 – NOTE this is the only pattern found so far that is NOT diagonally symmetrical (but works |
All |
All |
36 |
ZZ1 – horizontal 4 cell segments, start down |
All starting on ANY ODD column |
All starting on ANY ODD column |
37 |
ZZ2 – horizontal 4 cell segments, start up |
All starting on ANY ODD column |
All starting on ANY ODD column |
38 |
ZZ3 – horizontal 8 cell segment, then two 4-cell, start down |
None |
All starting on Any ODD row & column |
39 |
ZZ4 – horizontal 8 cell segment, then two 4-cell, start up |
None |
All starting on Any EVEN row & ODD column |
40 |
ZZ5 – Vertical 4 cell segments, start right |
All starting on rows 3, 7, 11, 15 |
All starting on rows 3, 7, 11, 15 |
41 |
ZZ6 – Vertical 4 cell segments, start left |
All starting on rows 2, 6, 10,, 14 |
All starting on rows 2, 6, 10, 14 |
42 |
ZZ7 – Horizontal, 2 cell segments, start down |
All starting on ODD columns |
All starting on ODD columns |
43 |
ZZ8 – Horizontal, 2 cell segments, start up |
All starting on ODD columns |
All starting on ODD columns |
44 |
ZZ9 – Vertical, 2 cell segments, start right |
All starting on ODD rows |
All starting on ODD rows |
45 |
ZZ10 – Vertical, 2 cell segments, start left |
All starting on EVEN rows |
All starting on EVEN rows |
46 |
ZZ11 – Horizontal, 6, 4, 2, 2 segments |
None |
Start on rows 3, 7, 11, 15 and ODD columns |
47 |
ZZ12 – Vertical, 6, 4, 2, 2 segments |
None |
Only some |
48 |
ZZ13 – 8 cell segments, horizontal, down/up |
All starting on ODD columns |
All starting on ODD columns |
49 |
ZZ14 – 8 cell segments, horizontal, up/down |
All starting on ODD columns |
All starting on ODD columns |
50 |
ZZ15 – 8 cell segments, vertical, right/left |
All starting only on rows 1 & 9 |
All starting on ODD rows |
51 |
ZZ16 – 8 cell segments, vertical, left/right |
All starting only on rows 8 & 16 |
All starting on EVEN rows |
52 |
Knight moves Diagonal, vertical right KM1 |
All |
All |
53 |
Knight moves Diagonal, vertical left KM2 |
All |
All |
54 |
Knight moves Diagonal, horizontal, down KM3 |
All |
All |
55 |
Knight moves Diagonal, horizontal, up KM4 |
All |
All |
56 |
LP1 – Large pattern # 1 |
All |
All |
57 |
LP2 – LP12 |
All |
All |
68 |
MP1 & MP2 | All | All |
Because the new 16 x 16 is pandiagonal magic and all 2 x 2 blocks sum
to n/4, it may be thought that this is a Most-perfect magic square. Alas! Cells spaced n/2
along the diagonals do not sum to n+1!
When summing a pattern of a row of 2 cells, within the same row (of 16 cells), there are
only two different sums and they alternate. Likewise, when summing a column of 2 adjacent
cells, the column of 16 cells will contain only two different (alternating) sums.
Here are the 12 small patterns mentioned in the comparison table
above. Each pattern consists of 16 cells arranged within one quadrant. Each pattern shown
may be started in any of the 256 cells of either Franklin 16 x 16 square because of the
continuous nature (wrap-around) of these squares.
Furthermore, because both squares may be altered by moving 4 rows or columns from 1 side
to the other, these patterns also appear 256 times in my version of the 16 x 16 square.
Every pattern I tested that was diagonally and orthogonally symmetrical, summed correctly, so presumably there are many more of this type then the 11 shown here. The only pattern I found that was not diagonally symmetrical but did sum correctly is shown as sp9.

All 12 patterns shown here sum correctly when started in any of the 256 cells of the original Franklin square, his newly discovered one, and my version of that one!
![]()
This image shows 12 large patterns of 16 cells. Each pattern consists
of 4 cells per quadrant with these cells placed symmetrical to the diagonal.
The image looks complicated but simply focus on one number/color at a time.
 |
Every pattern of this type that I checked summed correctly to 2056 for all 3 order-16 squares so presumably there are a great many more patterns possible. Because of wrap-around, the pattern may be started in any of the 256 cells of the square. For the original square, no 1/4 pattern summed to 1/4 S and no two 1/4 patterns summed to 1/2 S. When these patterns were tested on the new square and my version of it, results for several patterns were different, depending on which of the cells the pattern was started on. In some starting positions for patterns 5, 6 and 7, each of the four 1/4 patterns sum correctly to 1/4 S or the two pairs of 1/4 patterns each sum to 1/2 S. This is explained by the fact that these 1/4 patterns are 4 cell diagonals (see 3 and 4 in the comparison table). I did not find similar characteristics for any of the other nine patterns but did not test all patterns in all starting positions, so there is a possibility that some may exist. |
Two midsize patterns tested (MP1 & MP2) are 16 symmetrical cells within a 12x12 and
a 14x14 square.
I believe that ANY pattern of 16 cells that are fully symmetrical within a square area
from 6x6 to 16 x 16, will sum correctly when the pattern is started in ANY of the 256
cells of the Franklin square.
There is a magic square with similar features, but which includes 4 irregular patterns, on
my unusual squares page.
Shown here are 9 of the 16 zig-zag patterns tested. The other 7 patterns tested are reflections of these (reflections of 2 were not tested).
 |
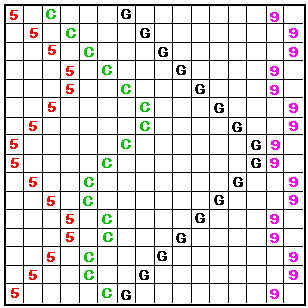 |
My test spreadsheets showed a number in each of the 64 cells of the square. This number was the total for the 16 cells whose pattern started on that cell. These patterns only sum correctly if started on the odd columns, so these columns all contain 2056. However, in most cases, the EVEN columns showed the incorrect totals as two alternating numbers.
# |
Original square |
New square |
ZZ1 |
The EVEN columns have alternating sums of 1800 and 2312 |
The EVEN columns have alternating sums of 2048 and 2064 |
ZZ2 |
The EVEN columns have alternating sums of 1800 and 2312 |
The EVEN columns have alternating sums of 2048 and 2064 |
ZZ7 |
The EVEN columns have alternating sums of 1800 and 2312 |
The EVEN columns have alternating sums of 1992 and 2120 |
ZZ8 |
The EVEN columns have alternating sums of 1800 and 2312 |
The EVEN columns have alternating sums of 1992 and 2120 |
ZZ9 |
|
The EVEN rows have alternating sums of 1800 and 2312 |
ZZ10 |
|
The ODD rows have alternating sums of 1800 and 2312 |
ZZ13 |
The EVEN columns have alternating sums of 1800 and 2312 |
The EVEN columns have alternating sums of 2048 and 2064 |
ZZ14 |
The EVEN columns have alternating sums of 1800 and 2312 |
The EVEN columns have alternating sums of 2048 and 2064 |
ZZ15 |
The EVEN columns have alternating sums of 1800 and 2312 |
The EVEN columns have alternating sums of 2048 and 2064 |
| ZZ16 | The ODD rows have alternating sums of 1928 and 2184 |
![]()
Knight move diagonals testedI tested 9 knight move patterns and found only 4 that sum correctly. However, undoubtedly there are more valid ones as yet undiscovered. Knight move 2 is a horizontal reflection of 1 and knight move 3 is a vertical reflection of 4. Keep in mind that the patterns shown in these diagrams do not represent the placement in the order-16 square. Each pattern may appear in that square in any position, subject to the conditions mentioned in the comparison summary table. |
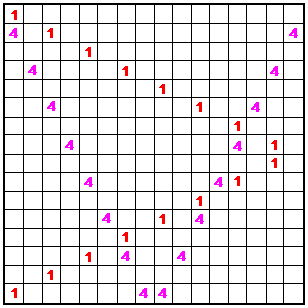 |
![]()
I show 12 small patterns (SP), 12 large patterns (LP), 16 bent diagonals (ZZ), and 4 knight move patterns (KN). All these patterns appear in all positions or many ordered positions in one or both of Franklin’s 16 x 16 squares as detailed in the comparison table
Be aware that there are many more such patterns. Maybe you will choose to investigate these fascinating squares further. If so, I would appreciate being advised of additional patterns that you find!
Franklin’s Squares |
|
| Order-8 Order-16 Magic Circle |
Both squares feature his famous ‘bent-diagonal’s’ but neither is magic in the accepted sense. All these were published in his lifetime, and many times since. |
| Order-8 | This is also bent-diagonal but not magic and was first published in 1959. |
| Order-4 Order-6 Order-16 |
These three squares have never been published prior
to The order-4 is actually a Disguised version of Frénicle’s # 175 magic square. It is associated but does not have bent diagonals. The order-6 is not magic but has bent diagonals. The order-16 is a pandiagonal magic square but also has many versions
of bent diagonals. It has many more magic patterns then the version Franklin published. |
![]()
Order-8 Franklin Squares Counted!
Recently Daniel Schindel,Matthew Rempel And Peter Loly (Winnipeg, Canada) counted the basic Franklin type bent-diagonal squares of order-8. [1]
There are exactly 1,105,920 of them. Two-thirds of these squares are not magic
because the main diagonals do not sum correctly.
Exactly one-third (368,640) are pandiagonal
magic.
BTW The Peter Loly's count has been
independently corroborated by other sources in Canada and Argentina.
An interesting report of this event appeared in
Ivars Peterson's Mathtrek column in
Science News Online
(June 24, 2006) [2]
This figure (368,640) is in exact agreement with that reported by Dame Kathleen Ollerenshaw as being most-perfect. The bent-diagonal pandiagonal squares all have the 2z2 feature (compact), but fail on the diagonal feature (complete) so we can assume that there are no order-8 bent-diagonal most-perfect magic squares!
Review of requirements to be classed as most-perfect: [3]
1. Doubly-even pandiagonal normal magic squares (i.e. order 4, 8, 12, etc using integers from 1 to m2)
2. Every 2 x 2 block of cells (including wrap-around) sum to 2T (where T= m2 + 1) (compact)
3. Any pair of integers distant ½m along a diagonal sum to T (complete)
Compact magic squares
All Franklin magic squares with correct main diagonals are pandiagonal magic.
They all have the compact feature (all 2x2 blocks of cells sum to 4/m of
S).
I have recently (May 2007) added a page explaining new findings of compact magic
squares. As examples, I compare 4 Franklin type order 8 squares. [4]
I have an Excel spreadsheet used in conjunction with this page. It is available
for downloading. [5]
[1] Proc.
R. Soc. A (2006) 462, 2271–2279, doi:10.1098/rspa.2006.1684. Enumerating the
bent diagonal squares of Dr Benjamin Franklin FRS
Published online 28 February 2006. Obtainable by download from Peter Loly's
home page
[2]
http://www.sciencenews.org/articles/20060624/ No
longer available?
[3] My Most-perfect page.
[4] My Compact magic squares page
[5] Compact_8-MS.xls on my Downloads.htm
![]()
Please send me Feedback about my Web
site!
![]()
![]()

![]()
Last updated
September 12, 2009
Harvey Heinz harveyheinz@shaw.ca
Copyright © 2001 by Harvey D. Heinz