 |
 |
 |
 |
 |
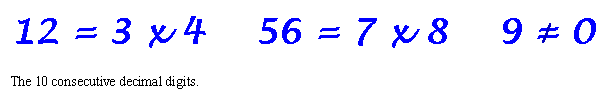
 This is a small sampling from my collection of over 400 patterns. I
hope you enjoy them.
This is a small sampling from my collection of over 400 patterns. I
hope you enjoy them.
And please call again soon.
Thanks to Dr. M. Ecker for adding the 9 <> 0 above.
See a picture of this pattern in cross-stitch, on my models page.
| Introduction | A brief explanation of what this page is all about. |
Relation of consecutive odd numbers to squares. |
The sum of N odd integers starting at 1 equals N squared. |
Relation of consecutive odd numbers to cubes |
The sum of N odd integers starting after the previous series equals N cubed. |
Four Related Patterns |
42, 342, 3342, etc. and three other similar numbers. |
1089 and it's reversal |
1089 x 9, 10989 x 9, etc., & their reversals x 4. |
Patterns with Primes |
A page with 50+ prime number patterns. |
More Prime Patterns |
Prime plots, Prime Queens problem, Prime rectangles, etc. |
Narcissistic Numbers |
Patterns where the number equals some manipulation of its digits. |
Palindromes |
A page of numbers that read the same backward as forward. |
|
New patterns added July 16, 2007 |
![]()
Herein are presented a miscellany of number patterns and interesting numbers. They are displayed with very little commentary but with the hope they will increase the viewer's appreciation for the beauty that can be seen in mathematics.
 NOTE
for elementary mathematics teachers; perhaps this material will be of value to your
students for mathematics enrichment.
NOTE
for elementary mathematics teachers; perhaps this material will be of value to your
students for mathematics enrichment.
Recreational mathematics hobbyists. Can you add material or insight to these patterns?
See my policy on this web site regarding credits at All About Credits
![]()

The sum of N odd integers starting at 1 equals N squared.
![]()

The sum of N odd integers starting after the previous series equals N cubed

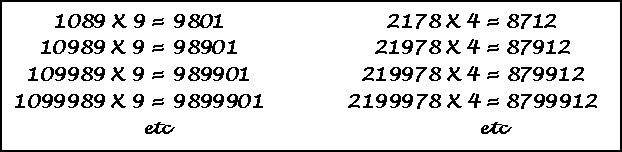
These are the only 4, 5, 6 and 7 digit numbers that are equal to a multiple of their
reversal.
(The series may be extended indefinitely by inserting nines into the center of each
number.)
Miscellaneous Patterns
17 = 23 + 32 This is the only number of the form x + pq + qp .
17 = 34 – 43 Is this the only number of the form x + pq - qp ?
JRM 30:3, page 234. Problem 2447 proposed by Michael Ried.
![]()
1729 = 103 + 93 = 123 + 13
Ramanujan
observed that this is the smallest number with this property.
Ramanujan’s number plus the number of the beast equals the sum of the first
prime and the squares of the next 9 primes.
1729 = 666 = 2 + 32 + 52 + 72 + 112 + 132 + 172 + 192 + 232 + 292 = 2395
Chanchal Singh, JRM 21:2, page 135. He also shows other facts about 1729.
![]()
27 x 594 = 16038
This is the only example of the 10 digits appearing in numbers of 2, 3, and 5
digits in this form.
Also, 594 is also an exact multiple of 27.
The Canterbury Puzzles, H. E. Dudeney, Dover Publ., 1958, Puzzle 101, Page 242
![]()
3816547290
is the
only base 10 number that…..
3
is evenly divisible by 1 Mike Kieth, REC #91 (vol.13, No.5), Jan. 1999, page 11. |
3608528850368400786036725
This is the
largest integer that has the property that it’s (Mike Kieth via email Jan. 20, 1999). |
![]()
|
(152
– 151 / 151) + 150 = 15 This works for any number. |
2 x 9 = 18
and 92 = 81 |
1/243 = 004113226337448559 |
![]()
|
124983/576
= 216.984375
digits 1 to 9 on each side of the equation. |
2340819/576
= 4063.921875
digits 0 to 9 on each side of the equation. |
![]()
91
= 9
92 = 81
and
8 + 1 = 9
93 = 729
and
7 + 2 + 9 = 18
and
1 + 8 = 9
94 = 6561
and
6 + 5 + 6 + 1 = 18
and
1 + 8 = 9
95 = 59049
and
5 + 9 + 0 + 4 + 9 = 27
and
2 + 7 = 9
This pattern
continues indefinitely .
This pattern looks good, but is the result of the simple fact that all multiples
of 9 have a digital root of 9.
Matt Medlock (via email Nov. 21, 2002).
![]()
(1 + 5
+ 4 + 7)(12 + 52 + 42 + 72) = 1547
(2 + 1 + 9 + 6)(22 + 12 + 92 + 62) =
2196
Other numbers with this property are 1, 133, 315, 803, and 1148.
Aktar Yalcin (via email June 25, 2007).
Please send me Feedback about my Web
site!![]()

![]()
Last updated
November 22, 2007
Harvey Heinz harveyheinz@shaw.ca
Copyright © 1998 by Harvey D. Heinz