 |
 |
 |
 |
 |

This palindromic prime number reads the same upside down or when viewed in a mirror.
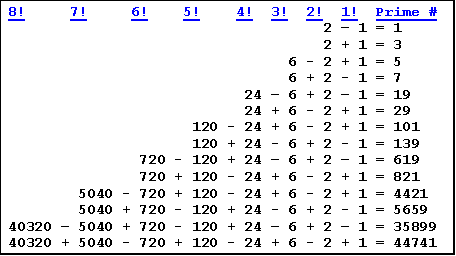
Factorial n (n!) means 1 x 2 x 3 x … x n
Unfortunately the next factorial results in a composite number.
The above shows the number 1 as a prime, although it is normally considered neither prime nor composite.
.
![]()
Assign the value 1 to A, 2 to B, 3 to C, . . . , 26 to Z. Then
![]() i.e.
16 + 18 + 9 + 13 + 5 = 61
i.e.
16 + 18 + 9 + 13 + 5 = 61
![]()
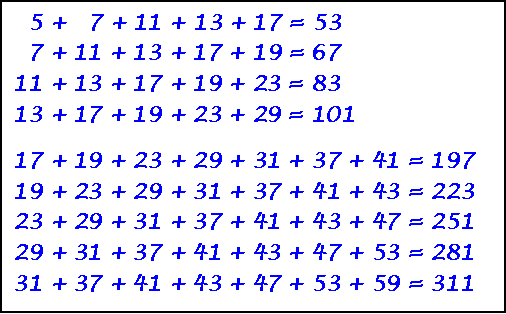
![]()

Above is shown three of the five series that use 2, the only even prime number.
Then I show one of each odd series from three to twenty-one. There are a total of sixty-one series with an odd number of primes (using primes < 100). every prime < 89 is the leading term in at least one series.
Charles w. Trigg, JRM 18(4),1985-86, p.247-248
![]()

All primes!
The next prime number in this series, though, is 17 threes with a one at the end.
Some other numbers in this series (with less then 1800 threes) are:
3391 (that's 39 threes with a one at the end
37831
317311
Near Repdigit Primes consist of a series of the same digit, then one different digit; or
one digit and then a series of a different digit.
The above series is particularly attractive because the number of threes in the first
seven primes increase by one. There are only eleven other primes in this series with less
then 1800 threes.
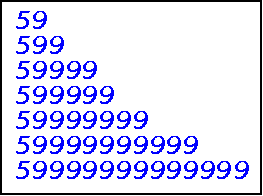 This is an example of the other type of Near Repdigit Primes.
This is an example of the other type of Near Repdigit Primes.
Some other numbers in this series (with less then 4471 nines) are:
5922
59361
594332
This last number is a prime consisting of a five followed by 4,332 nines!
There are many combinations of digits that make up Near Repdigit Primes but the last digit
in the number must be a 1, 3, 7, or 9.
![]()

of digit length from 1 to 15
![]()

The above two primes evenly divide the sum of the primes less then themselves.
The only other such prime less then 2,000,000 is 369119, the 1577th prime.
D. Wells, Curious & Interesting Numbers P.129
![]()
Starting with 2 , find product of consecutive primes. Call it p
Then p + 1 = s
Take next largest prime > s. Call it v.
Then v – p = prime.
Martin Gardner (The Last Recreations) calls these last numbers ‘fortunate
primes’.

![]()

For k = 1,2,6, & 38. The next prime has at least 500 digits !
![]()

Three consecutive primes sum to a palindromic prime.
Visit Patrick De Geest's very attractive and informative WWW site about Palindromic
Numbers at Other Links
The 9-digit set was reported by Jud McCranie July 11, 1998
![]()

The 21 consecutive primes from 7 to 89 sum to the prime number 953. Also when arranged in groups of three, each group sums to a prime. Furthermore, the reverse of these prime sums also sum to 953 !
T.V.Padmakrumar, JRM 27:1, 1995, p57
![]()

11 is the only Palindromic prime with an even number of digits.
These are the smallest and largest Palindromic primes of length 1 to 19.
Number of palindromic primes of length 1=4, 2=1, 3=15, 5=93, 7=668, 9=5172
From PALPRI..HTM by Patrick De Geese, Belguim, July/96

FromPALPRI..HTMbyPatrickDeGeese,Belguim,July/96
Link to his page from Other Links
Product of the first eight primes divided by ten gives a palindrome number.

| Palindromic Primes | There are a total of 5172 nine digit primes that read the same forward or backward. Many of them have extra properties. |
| Plateau Primes | There are 3 primes where all the interior digits are alike and are higher then the terminal digits. There are two primes, 322222223 & 722222227 in which the interior digits are smaller then the end ones. These are called Depression Primes |
| Undulating Primes | So called when adjacent digits are alternately greater or less then their neighbors. If there are only two distinct digits, they are called smoothly undulating. Of the total of 1006 undulating nine digit palindromic primes, seven are smoothly undulating. |
| Peak & Valley Primes | If the digits of the prime, reading left to right, steadily increase to a maximum value, and then steadily decrease, they are called peak primes. Valley primes are just the opposite. There are a total of 10 peak and 20 valley primes. 345676543 is unique because of the five consecutive digits. |
 The above numbers are called depression primes. The next ones in
the 'two' series contain 27 and 63 two's! Note the 'seven 'two's in the one above. The
next ones in the 'five' series contain 19, 21, 57, 73 & 81 fives.
The above numbers are called depression primes. The next ones in
the 'two' series contain 27 and 63 two's! Note the 'seven 'two's in the one above. The
next ones in the 'five' series contain 19, 21, 57, 73 & 81 fives.
![]()
 This 19 digit number reads the same forwards and backwards. It
contains each of the digits 0 to 9 twice, except the 7 which appears only once .
This 19 digit number reads the same forwards and backwards. It
contains each of the digits 0 to 9 twice, except the 7 which appears only once .
![]()
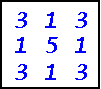 1 of the 24 possible order-3 perfect prime squares (not counting
rotations and reflections. Each row, column, and the two main diagonals all consist of
3-digit primes when read in either direction. This one is superperfect because the
broken diagonal pairs are also 3-digit prime numbers. The 5 can be replaced with
an 8. These are the only order-3 Superperfect prime squares.
1 of the 24 possible order-3 perfect prime squares (not counting
rotations and reflections. Each row, column, and the two main diagonals all consist of
3-digit primes when read in either direction. This one is superperfect because the
broken diagonal pairs are also 3-digit prime numbers. The 5 can be replaced with
an 8. These are the only order-3 Superperfect prime squares.
All order 2 and 3 perfect prime squares contain palindromes and contain duplicate prime numbers.
Do only Order-3 perfect prime squares contain palindromic primes? Are there any superperfect prime squares of order greater then 3?Charles W. Trigg,Perfect Prime Squares, JRM 17:2, 1984-85, pp .91-94, 1984-85
Addendum August 31, 2007
Søren Schandorf and his associates in Denmark have been working on this problem. Yesterday I received the list of order-5 Perfect Palindromic Prime Squares (PPPS). And some solutions for the order-7. Here I show two examples from his report.
Each order-5 PPPS contains seven 5 digit palindromic primes, and each order-7 square contains nine 7 digit palindromic primes.
See their report on this project at http://www.chronomatics.dk/sppps-5.pdf
Søren also confirmed that the two order-3 SPPPS shown on this page are the only ones of that order. His group found 182 squares for order-5 and an astounding 614,157 for order 7.
![]()

Each sequence is formed from the one above it by inserting n, the row number, between all adjacent numbers that add to n. k is the number of numbers in each sequence. So far all k are prime numbers. Does this series continue indefinitely?
This pattern is credited to Leo Moser (Martin Gardner, The Last Recreations, p.199).

373 = sum of the squares of the first 5 odd primes
Also: the sum of five consecutive primes starting with 67.
From Patrick De Geest's Palindrome numbers WWW site at http://www.worldofnumbers.com/
![]()

This prime contains all the digits from 1 to 9 in order, then repeats starting from 0.
Two similar primes but using only the nine digits from 1 to 9 are 1234567891 and
1234567891234567891234567891.
David Wells, Curious & Interesting Numbers, p191

These numbers are all primes!!
3911, it's reverse, and both numbers with a 3 on either end or a 9 on either end.
There are a total of 102 reversible prime pairs of four digits.
![]()

These primes are six digit reversable with an imbedded four digit reversable prime.
For example, the top number of the middle column: following are all prime; 311537, 335117,
735113, 711533, 1153, 3511..In this particular case, 31153, 71153 and 35117 are five digit
primes, 11 and 53 are two digit primes, and two 3’s, the 5 and the 7 are all one
digit primes.
There are a total of 4769 reversible prime pairs of six digits.

In each of these two squares, all rows, columns and the two main diagonals are distinct prime numbers when read in either direction. The order-5 square above is one of three reported by Mr. Card.
L. E. Card,Patterns in Primes, JRM 1:2, 1968, pp .93-99,
![]()
 In 1998 Carlos B. Rivera and Jaime Ayala rediscovered the order-4 shown above
(L. E. Card) and conjecture that it is the only solution with 20 distinct primes and no
palindromes. They also found another three order-5 Perfect Prime Squares with 24 distinct
5 digit primes (they call them Prime-magical squares). They also found these two order-6
squares which each contain twenty-eight 6 digit primes.
In 1998 Carlos B. Rivera and Jaime Ayala rediscovered the order-4 shown above
(L. E. Card) and conjecture that it is the only solution with 20 distinct primes and no
palindromes. They also found another three order-5 Perfect Prime Squares with 24 distinct
5 digit primes (they call them Prime-magical squares). They also found these two order-6
squares which each contain twenty-eight 6 digit primes.
Carlos has a WWW page dealing with Prime Puzzles & Problems at http://www.sci.net.mx/~crivera/.
Digit Complementary Prime Pairs

A Diigit Complementary Prime Pair is defined as a pair of prime numbers in which digits in corresponding positions sum to 10 (or 0). There are 136 four digit pairs.
a.
a reversible prime pair b. the two primes contain 8 different digitsCharles W. Trigg, JRM 22:2, 1990, p 95-97
![]()

This is an example of a prime circle. Two adjacent numbers, including the last number and the first number, sum to a prime. In this particular case all the numbers are 3 digits. This circle is of length ninety, and is part of a 200 length prime circle found by Charles Ashbacher, JRM 26:1, 1994, p 63.
![]()
 Start at the first digit, or the first digit after any comma, and
read a nine digit prime number.
Start at the first digit, or the first digit after any comma, and
read a nine digit prime number.
 The only 3-digit numbers such that all arrangements of their three digits are
prime numbers.
The only 3-digit numbers such that all arrangements of their three digits are
prime numbers.
Also for 113, all 2-digit combinations are prime numbers.
![]()
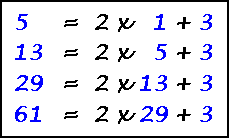
The prime factors of 114985 are 1, 5, 13, 29, 61.
![]()

The above three numbers are all Pluperfect Digital Invariants, meaning that when each digit of the number is raised to the power equal to the length of the number, the sum of these powers is equal to the original number.
i.e. 28116440335967 = 214 + 814 + 114 + 114 + 614 + 414 + 414 + 014 + 314 + 314 + 514 + 914 + 614 + 714.
The above three numbers are also PRIME !
They are the only primes among the 79 PPDI’s under length forty.
The first number (the smallest) is the only one of the three that is pandigital. Also, of the four digits that appear twice, three
appear as adjacent pairs.
The largest number contains three digits that appear four times and three digits that
appear three times.
See Deimel & Jones, JRM 14(2), 1982, pp. 87 to 99 for list of the 79 PPDI’S to order 39.

Addendum: January, 2006
Luis Rodriguez advised me of another series of primes separated by 0, 2, 4, 6,
..., 26.
The prime number 484511389338941 will produce a string of 14 prime numbers with
gaps the size of the above digits.
![]()
 All the numbers in these pyramids are primes.
All the numbers in these pyramids are primes.
Also...
All the numbers in the first pyramid are reversible primes. All numbers in the second
pyramid except the fourth and sixth ones (8 & 12 digits) are also reversible primes.
(The next number in each sequence is composite).
![]()

The largest known prime number such that any two adjacent digits are prime and all these primes are different.
David Wells ,Curious and Interesting Number, p. 195
 |
These are the largest possible primes with this property. The
top number of the second column as shown on page 191 of the credit is a typo, as the
number shown is composite. In the third set, the last digit of the first number could be a
three, as that number is also a prime. The number ‘1’ here is presumed to be
prime, although by definition it is not. Four other numbers with this property are 233399339, 29399999, 37337999 & 59393339 Chris K. Caldwell, Journal of Recreational Mathematics, 19:1, 1987,pp 30-33 David Wells, Curious & Interesting Numbers pps 191, 192, 200 |
 |

![]()

Unfortunately, these relationships do not hold for the next higher prime, 19.
![]()
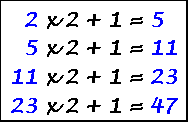
(Term n = Term n-1 times 2 plus 1)
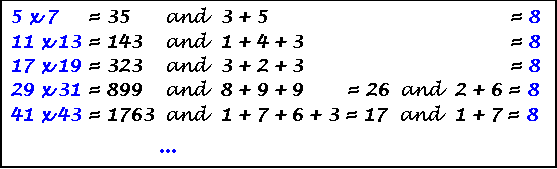
![]()

These are all the 12-digit primes of this type.
There is 1 with 3 digits, 1 with 5 digits, 1 with 6 digits,
2 with 8 digits, and 1 with 9 digits.
Next size after 12 digits is 17 with 2 such prime numbers.
C. Caldwell & H.Dubner JRM 27:1, 1995, p 35
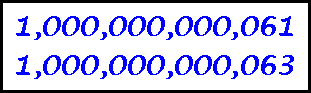 The two largest known twin primes are 242206083 * 238880 . plus and
minus 1 with 11713 digits, found by Indlekofer and Ja'rai in November, 1995. They are also
the first known gigantic twin primes (primes with at least 10,000 digits).
The two largest known twin primes are 242206083 * 238880 . plus and
minus 1 with 11713 digits, found by Indlekofer and Ja'rai in November, 1995. They are also
the first known gigantic twin primes (primes with at least 10,000 digits).
See http://www.utm.edu/research/primes/lists/top20/twin.html
![]()
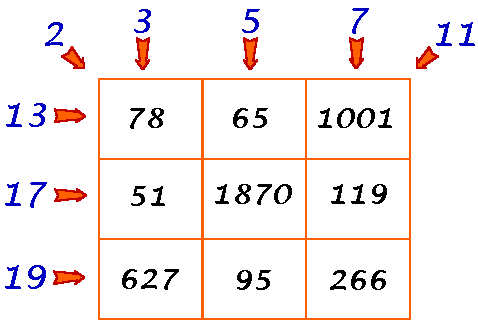
Each row, column and main diagonal has a common factor that is one of the first 8 prime numbers.

A circular prime is a prime number that remains prime as each leftmost digit (msd)
in turn is moved to the right hand side.
From Patrick De Geest's Palindrome numbers WWW site (see above)
![]()
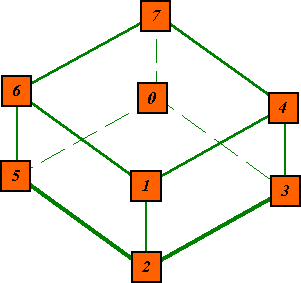
The only arrangement of 8 consecutive digits (not counting rotations or reflections) such that any two adjacent sum to a prime number.
![]()
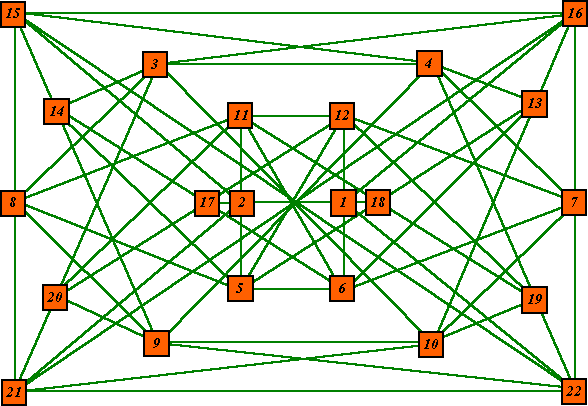
In this pattern the sum of each pair of numbers connected by a line sums to a prime
number.
The pattern is symmetrical both horizontally and vertically and uses the consecutive
numbers from 1 to 22.
![]()
Please send me Feedback about my Web
site!
![]()
![]()

![]()
Last updated
December 21, 2007
Harvey Heinz harveyheinz@shaw.ca
Copyright © 1998, 2000 by Harvey D. Heinz