 |
 |
 |
 |
 |
Recreational & Educational Computing is a 14 to 18 page newsletter published 6 times a year by Dr. Michael Ecker.
REC Focus: Stimulating mathematics, recreation, education, programming, graphics, and other computer activity.
Dr. Ecker has several subsidiary programs to compliment REC, such as:
REC-on-Disk which includes the paper version
plus all programs plus additional material
Mathematical Farragoes each of which are
multiple disk collections of contributed programs.
More information at:
Visit REC's web site at http://members.aol.com/DrMWEcker/REC.html
Or contact Dr. M. W. Ecker via e-mail at MWE1@PSU.edu or DrMWEcker@AOL.com
I thank Dr. Ecker for permission to show here several magic squares previously
published in REC.
And , of course, I thank the authors for their ingenuity and hard work.
| Order-5 Palindrome Magic square | Order-4 and order-5 magic squares consisting only of palindromes. |
| Consecutive Prime Numbers Order-9 | An order-9 magic square consisting of 81 consecutive primes. |
| Forty-one | This order-11 magic square includes 41 fortyones. |
| E.S.-71 | This order-16 magic square includes the authors initials and year of construction. |
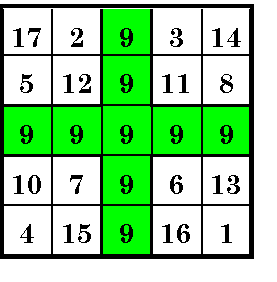
| Number-Nine Magic Square | An order-4 magic square changed into an order-5 by adding 8 additionaal nines. |
| Order-16 Prime Number Magic Square | With inlaid orders 4, 6, 8, 10, 12, 14 magic squares of primes. |
Order-6 Prime Magic Star |
This star uses 19 consecutive prime numbers in 9 lines of 5. |
![]()
 Alan W.
Johnson, Jr., REC vol.5, No. 8. December 1990,Page 4
Alan W.
Johnson, Jr., REC vol.5, No. 8. December 1990,Page 4
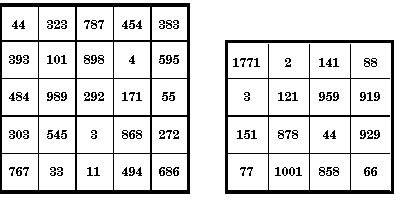
Written to celebrate the palindromic year 1991., the 25 palindromes of this order-5 square have the magic sum 1991.
Adding 11 (another palindrome) to 1991 gives the next palindrome year 2002, the sum of this order-4 magic square. It consists of 16 different palindromes
![]()
Alan W. Johnson, Jr., REC vol. 7 No. 7. February1993,Page 10
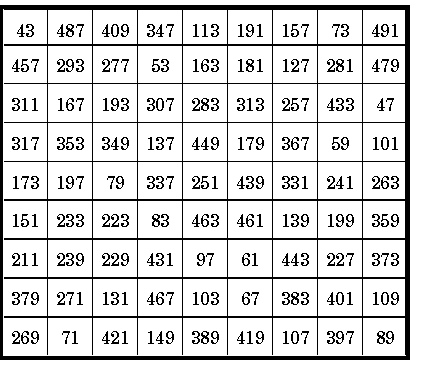
This order-9 magic square is composed of the 81 consecutive prime numbers 43 to 491. The magic sum is the prime number 2311.
![]()
E. W. Shineman, Jr., REC vol.8 No. 1 & 2. July 1993,Page 5
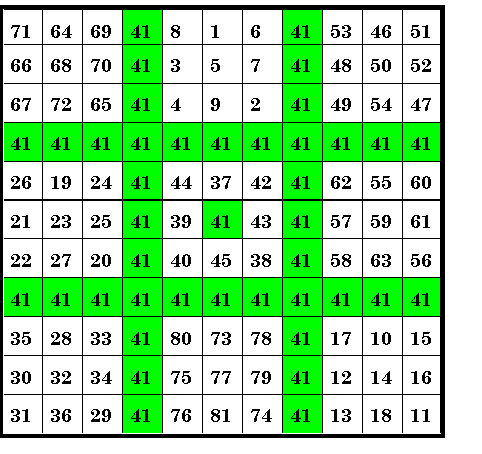
This order-11 magic square consists of a normal order-9 composite magic square divided into it's nine order-3 magic squares with 40 additional forty-ones. The magic constant is 11 x 41. Mr. Shineman constructed this square to celibrate the year 1941!
The magic constant of each of the nine order-3 magic squares themselves form an order-3
magic square, a feature of all composite magic squares.
The principal holds for any number substituted for 41, as long as the starting number is
such that the middle number of the series is the number you wish to substitute for 41.
 E. W.
Shineman, Jr., REC vol.8 No. 3 & 4. July/August/September 1993,Page 17
E. W.
Shineman, Jr., REC vol.8 No. 3 & 4. July/August/September 1993,Page 17
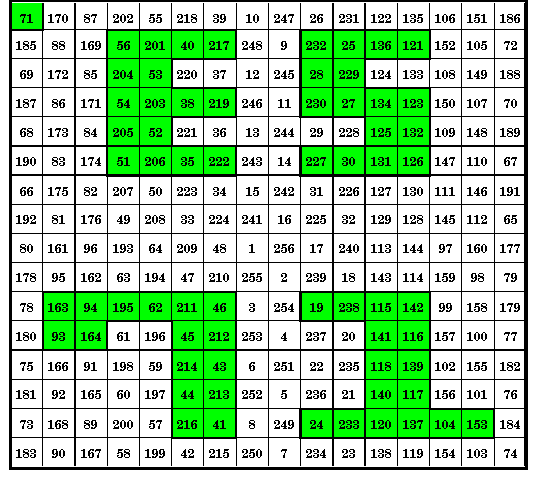
This order-16 magic square is pandiagonal so broken diagonals also sum to the constant 2056, as well as each of the authors initials and the two figures of the year of creation (1971).
It may also be considered an ornate magic square because of the inlaid figures (E, S, 7 and 1). Of course, if you make use of the pandiagonal feature to tranform it to a different magic square by moving columns or rows from one side to the other , this ornate feature would disappear.
![]()
 E. W.
Shineman, Jr., REC vol.10 No. 3 & 4. December 1995-January 1996,Page 1
E. W.
Shineman, Jr., REC vol.10 No. 3 & 4. December 1995-January 1996,Page 1
An order-5 magic square constructed from the series of numbers from 1 to 17, but with 8 additional (total of 9) nines .
The magic sum = 45. Note that 9 = 4 + 5 which is also the two orders involved. Also, the outer four order-2 squares are not magic but the four cells of each sum to 36 and 3 + 6 = 9.
This is classified as an ornate magic square. It is not a pure or normal one
because it doesn't consist of a series of numbers from 1 to n2.
![]()
Alan W. Johnson, Jr., REC vol.6, No. 1 & 2. March 1991,Page 13
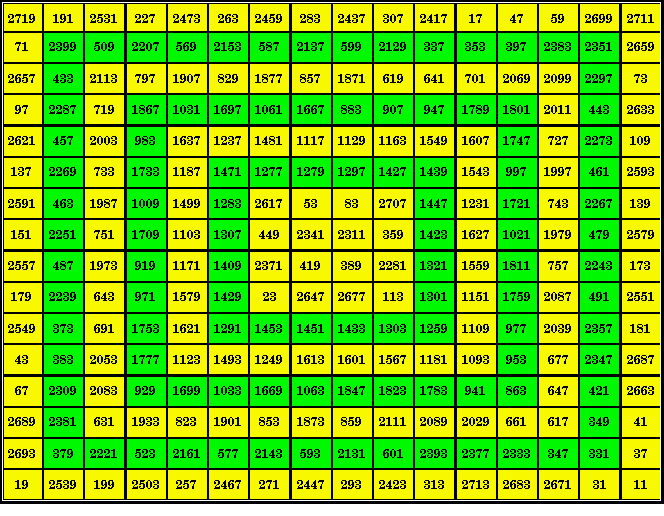
This magic square contains inlays of each even order magic square from 4 to 14. It looks like a concentric or bordered magic square, but this square has the low and high numbers scattered throughout the square. With a true bordered magic square, one half the numbers in the border consists of the low numbers in the series, the other half are the high numbers.
Here each square has all rows, columns and main diagonals equal to the
magic constant for that square, as follows:
Order-4 5460
Order-10 13650
Order-14 19110
Order-6 8190
Order-12 16380
Order-16 21840
Order-8 10920
The magic sums differ by a constant 2730.
![]()
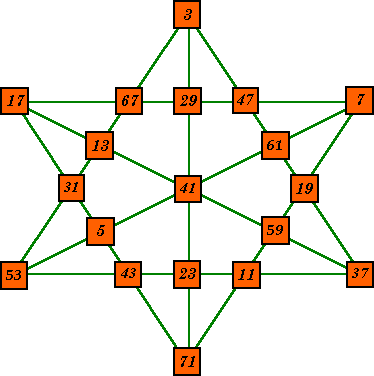 |
This magic star uses the prime numbers from 3 to 71. Each of the 9 lines
of 5 numbers sums to the prime number 167. It was designed by Allan Wm. Johnson, Jr. of Washington, DC and was published in Recreational & Educational Computing, Vol. 15, Nos. 2 & 3, page 21. Used by permission. |
Please send me Feedback about my Web
site!![]()
![]()

![]()
Harvey Heinz harveyheinz@shaw.ca
This page last updated
September 10, 2003
Copyright © 1998, 1999 by Harvey D. Heinz