 |
 |
 |
 |
 |
A pattern closely related to magic squares but relatively unexplored, is the anti-magic square.
Here we present some examples of them and their sibling, the heterosquare.
Heterosquare: similar to a magic square except all rows, columns and
main diagonals have different sums.
Anti-magic Square: similar to a heterosquare except all rows, columns and
main diagonals have consecutive sums.
Antimagic Squares |
Orders 4 to 9. Rows, columns and diagonals sum different but are consecutive. |
Order-10 Anti-Magic Squares |
This special anti-magic square has the numbers 19 & 99 in the central bottom cells. |
Order-3 Heterosquares |
12 different squares. Each of the 8 lines has a different sum. Also orders 4, 5, 6.. |
Peter Bartsch's Heterosquares |
This material added March 28/03. Real and prime heterosquares. |
Enoch Haga’s Prime Heterosquares |
The rarity of these special patterns may surprise you (May, 2004). |
Anurag Sahay's Prime Heterosquares |
Download an Excel spreadsheet listing many heterosquare and anti-magic squares. |
![]()
Anti-magic squares are a subset of heterosquares were the row, column, and diagonal sums are consecutive integers. These six use the consecutive digits from 1 to n2. Because they are anti-magic squares, the sums are consecutive numbers.
They are much more difficult to construct then heterosquares. There are no order 3 anti-magic squares. As the order increases, construction becomes easier , although there doesn't seem to be any standard routine available for constructing them.
Addendum: John Cormie developed several methods in 1999 for generating
antimagic squares. See note in next section.
J. Lindon introduced the subject and published orders 4 to 9 antimagic squares
(different then those shown here) in 1962.
|
Order-8 S = 251 - 268 |
260 |
|||||||||||||||||||||||
|
Order-7 S = 167 - 182 |
175 |
9 |
41 |
37 |
46 |
55 |
15 |
49 |
16 |
268 |
||||||||||||||
|
19 |
8 |
32 |
18 |
22 |
48 |
35 |
182 |
60 |
10 |
27 |
21 |
50 |
54 |
22 |
23 |
267 |
||||||||
|
11 |
33 |
10 |
30 |
43 |
15 |
27 |
169 |
2 |
59 |
28 |
56 |
19 |
17 |
44 |
40 |
265 |
||||||||
|
Order-4 29 - 38 |
34 |
46 |
9 |
13 |
14 |
17 |
23 |
49 |
171 |
64 |
13 |
35 |
14 |
25 |
57 |
18 |
36 |
262 |
||||||
|
2 |
15 |
5 |
13 |
35 |
40 |
45 |
39 |
12 |
1 |
4 |
31 |
172 |
3 |
63 |
31 |
45 |
42 |
11 |
43 |
20 |
258 |
|||
|
16 |
3 |
7 |
12 |
38 |
20 |
2 |
26 |
42 |
38 |
41 |
5 |
174 |
52 |
4 |
39 |
24 |
32 |
47 |
6 |
51 |
255 |
|||
|
9 |
8 |
14 |
1 |
32 |
7 |
34 |
37 |
25 |
44 |
24 |
6 |
177 |
30 |
62 |
1 |
38 |
33 |
7 |
53 |
29 |
253 |
|||
|
6 |
4 |
11 |
10 |
31 |
36 |
47 |
16 |
29 |
3 |
21 |
28 |
180 |
34 |
5 |
61 |
12 |
8 |
58 |
26 |
48 |
252 |
|||
|
33 |
30 |
37 |
36 |
29 |
179 |
178 |
173 |
170 |
168 |
176 |
181 |
167 |
... |
254 |
257 |
259 |
256 |
264 |
266 |
261 |
263 |
251 |
||
|
Order-9 S = 359 - 378 |
369 |
|||||||||||||||||||||||
|
6 |
51 |
40 |
67 |
53 |
60 |
1 |
63 |
30 |
371 |
|||||||||||||||
|
66 |
49 |
57 |
3 |
28 |
59 |
15 |
72 |
21 |
370 |
|||||||||||||||
|
Order-6 S = 104 - 117 |
111 |
7 |
35 |
31 |
81 |
44 |
58 |
11 |
73 |
25 |
365 |
|||||||||||||
|
Order-5 S = 60 - 71 |
65 |
3 |
18 |
36 |
17 |
15 |
27 |
116 |
70 |
55 |
69 |
5 |
16 |
13 |
75 |
4 |
56 |
363 |
||||||
|
5 |
8 |
20 |
9 |
22 |
64 |
23 |
32 |
6 |
10 |
30 |
12 |
113 |
18 |
27 |
33 |
65 |
45 |
62 |
8 |
61 |
43 |
362 |
||
|
19 |
23 |
13 |
10 |
2 |
67 |
35 |
1 |
14 |
19 |
34 |
5 |
108 |
42 |
41 |
9 |
48 |
32 |
20 |
78 |
17 |
74 |
361 |
||
|
21 |
6 |
3 |
15 |
25 |
70 |
33 |
25 |
4 |
11 |
13 |
24 |
110 |
76 |
38 |
47 |
10 |
68 |
19 |
80 |
14 |
26 |
378 |
||
|
11 |
18 |
7 |
24 |
1 |
61 |
2 |
22 |
20 |
26 |
16 |
21 |
107 |
24 |
39 |
36 |
79 |
46 |
50 |
22 |
52 |
29 |
377 |
||
|
12 |
14 |
17 |
4 |
16 |
63 |
9 |
8 |
29 |
31 |
7 |
28 |
112 |
64 |
37 |
54 |
2 |
34 |
23 |
77 |
12 |
71 |
374 |
||
|
68 |
69 |
60 |
62 |
66 |
71 |
105 |
106 |
109 |
114 |
115 |
117 |
104 |
373 |
372 |
376 |
360 |
366 |
364 |
367 |
368 |
375 |
359 |
||
![]()
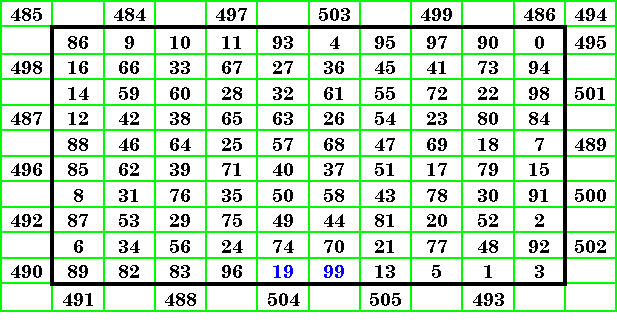
A present day Anti-Magic analogue to Durer's 1514 magic square. This one for the year 1999.
This square appears on the Table of Contents page of John Cormie and
Václav Linek ’s excellent Antimagic Squares site.
Notice that the 22 line, column and diagonal totals are the consecutive numbers from 484
to 505.
A heterosquare was defined in Mathematics Magazine, 1951, as an x by x array of integers from 1 to n2 such that all rows, columns and main diagonals have different sums.
In these twelve 3 x 3 heterosquares, the 3 rows, 3 columns, and 2 diagonals all have
unique arrangements of different sums.
Are there any other basic arrangements?

Examples of order 4, 5, and 6 heterosquares (one of the many possible for each order).
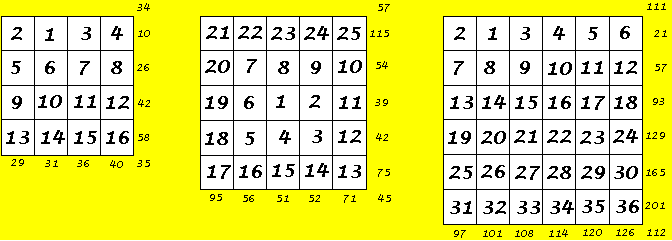
The even orders are simply constructed by entering the numbers in order, then changing the positions of numbers 1 and 2.
The order 5 (or any odd order) is constructed by entering the numbers in order in a spiral starting with the center cell (or a corner cell).
References.
J. A. Lindon, Anti-magic Squares,
Recreational Mathematics Magazine, No. 7, Feb. 1962, pp16-19
J. S. Madachy, Mathematics on Vacation, Thomas Nelson & Sons, 1996, pp 101-110
John Cormie and Václav Linek ’s excellent Antimagic Squares
site. Sorry, this site is no longer available. Try
http://io.uwinnipeg.ca/~vlinek/jcormie/ at
http://web.archive.org/
Introduction
Are there other basic arrangements?
The question I asked originally when I presented the 12
heterosquares above was answered by Peter Bartsch, in correspondence starting in
Nov., 2002.
The following is condensed from material supplied by him.
He reports that there are 3120 different basic (no rotations or reflections) heterosquares of order 3 using the numbers 1 to 9.
He coined the term ‘real’ for those heteroquares that consist of 17 distinct numbers, 9 for the interior numbers and 8 for the line sums. It turns out there are only 760 real heterosquares using the integers 1 to 9. Only two of the 12 heterosquares I show above are ‘real’!
The following 22 order 3 heteroquares are from the list of 760 real order 3 heteroquares. Each has a different grand total, which is the sum of the 9 interior numbers and the 8 line sum numbers. These totals range between 111 and 133, with none totalling 112.
The line sums contain anywhere from 2 to 7 consecutive numbers. None have all eight sums consecutive. They would then be antimagic squares, and there are no antimagic squares of order 3!

Summary
There are 3120
basic heterosquares (HS) of order 3 using the numbers 1 to 9. Of these, 760 are
real HS.
414 basic HS have two consecutive numbers in the sums. 1352 have 3 consecutive
numbers, 816 have 4 consecutive numbers, 374 have 5, 126 have 6, and 38 HS have
7 sums in consecutive order.
This material was supplied by Peter Bartsch between
November 2002 and March 2003.
Note that the first two are by Carlos Rivera [1], the third one by Jean-Charles
Meyrignac.
Meyrignac's solution is believed to be the smallest possible order 3 prime
heterosquare.

[1] Problem 69 of Carlos Rivera's http://www.primepuzzles.net/
![]()
The following six heterosquares use the 9 consecutive primes from 31 to 67, so the total of these 9 cells is always 439 (a prime).
The 8 line sums
are all primes in the range from 109 to 181.
Their sums form the totals, 1621, 1637, 1653, 1621, 1583, 1601. All are prime
except 1653.
The squares are displayed and arranged according to Frenicle's index method.
Actually, Peter had sent many more examples, but all proved to be disguised
versions of these six.

Contact Peter Bartsch at pbartsch@synstar.de
See my page on Prime magic squares.
![]()
|
On May 3,
2004, I received from Enoch Haga, two order 3 heteromagic squares
consisting of prime numbers. |
 |
As expected, these patterns are quite rare. However, it may
come as a surprise to see just how rare they are!
In Enoch’s search, he keeps a running count of the groups of 9 primes that he
checks.
The primes from 2 to 23 is count 1, 3 to 29 is count 2, etc.
The first group of 9 consecutive primes that form a
heterosquare when placed in order in the above pattern occurs at count 130,495!
Another way to say this is that 1,734,133 is the 130,495th prime.

For those that are interested, Enoch has provided a Ubasic listing of a program to find the second solution.
![]()
On May 6, 2004 I received another email from Enoch. I quote.
Actually, because no primality test is made for the sums of the
middle row and column, these squares are not necessarily PRIME heterosquares.
In both of these examples, both of these sums are composite. However, both are
still heterosquares.
![]()
| On May 10, 2004 Enoch produced his first order 5 prime
ring heterosquare. It consists of 25 consecutive primes arranged in a
spiral pattern starting with 136143131 in the center (hub) cell. The 2 outside rows, the 2 outside columns and the 2 diagonal sums are all primes as well as the totals of these and the hub. Because most of the interior rows and columns are composite numbers, this is a composite heterosquare. |
 |
![]()
Program to find the second solution for Enoch’s regular heterosquares.
10 ' pr3sq, 16 Apr 2004, Enoch Haga 15 ' nxtprm(x) = get next prime number after x 16 ' prmdiv(x) = is x prime? 20 Q=Q+2531718:N=41720069 30 A=nxtprm(N) 40 B=nxtprm(A) 50 C=nxtprm(B) 60 D=nxtprm(C) 70 E=nxtprm(D) 80 F=nxtprm(E) 90 G=nxtprm(F) 100 H=nxtprm(G) 110 I=nxtprm(H) 120 J=I+B+C 130 K=H+A+D 140 L=G+F+E 150 M=I+H+G:O=B+A+F:P=C+D+E 160 Y=I+A+E:Z=G+A+C 165 Zz=J+K+L+M+O+P+Y+Z:if Zz=prmdiv(Zz) then stop 170 if J=prmdiv(J) and K=prmdiv(K) and L=prmdiv(L) then V=V+1 180 if M=prmdiv(M) and O=prmdiv(O) and P=prmdiv(P) then V=V+1 190 if Y=prmdiv(Y) and Z=prmdiv(Z) then V=V+1 200 if V<3 then 260 210 if V=3 then print I;B;C;J 220 if V=3 then print H;A;D;K 230 if V=3 then print G;F;E;L 240 if V=3 then print M;O;P 250 if V=3 then print Y;Z;"Count =";Q:stop 260 A=nxtprm(A) 270 Q=Q+1 280 V=0 290 goto 40
![]()
An order-4 pandiagonal anti-magic square is shown on my newer Still More Magic Squares page.
Thanks again for the visit and I hope to see you again soon.

![]() Please send me Feedback about my Web site!
Please send me Feedback about my Web site!![]()

![]()
Harvey Heinz harveyheinz@shaw.ca
This page last updated
October 31, 2009
Copyright © 1998, 1999 by Harvey D. Heinz