

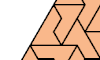
 | Tiling a Triangle with a Polyiamond. Tile a triangular polyiamond with copies of a given polyiamond. |
 | Tiling a Triangle with Two Polyiamonds. Tile a triangular polyiamond with copies of two given polyiamonds. |
 | Tiling a Triangle with a Scaled Polyiamond. Tile a triangular polyiamond with copies of a given polyiamond at various scales. |
 | Tiling a Triangle with a Scaled Polyming. Arrange scaled copies of a polyming to form a triangle. |
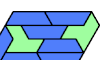 | Pentiamond-Hexiamond Pair Pentagons. Arrange copies of a pentiamond and a hexiamond to form a polygon with 5 sides. |
 | Tiling a Pentagon with a Scaled Pentiamond and Hexiamond. Arrange scaled copies of a pentiamond and a hexiamond to form a polygon with 5 sides. |
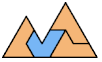 | Hexiamond Pair Pentagons. Arrange copies of two hexiamonds to form a polygon with 5 sides. |
 | Pentiamond-Heptiamond Pair Pentagons. Arrange copies of a pentiamond and a heptiamond to form a polygon with 5 sides. |
 | Heptiamond Pair Pentagons. Arrange copies of two heptiamonds to form a polygon with 5 sides. |
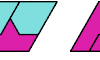 | Heptiamond Pair Parallelograms. Tile a parallelogram with copies of two heptiamonds. |
 | Two-Hexiamond Balanced Hexagons. Tile a regular hexagon with two hexiamonds in equal quantities. |
 | Tiling Regular Hexagons with Scaled Hexiamond Pairs. Tile a regular hexagon with two hexiamonds that may be freely scaled up. |
 | Tiling a Regular Hexagon with a Scaled Pentiamond and Hexiamond. Tile a regular hexagon with a pentiamond and a hexiamond that may be freely scaled up. |
 | Tiling a Regular Hexagon with Three Hexiamonds. Tile a regular hexagon with copies of three different hexiamonds. |
 | Polyiamond Hexagon Tiling. Tile a straight or ragged hexagon with various polyiamonds. |
 | Holey Polyiamond Hexagon Tilings. Tile a regular hexagon with a polyiamond, allowing isolated moniamond holes. |
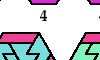 | Tiling a Holey Regular Hexagon with Two Hexiamonds. Tile a regular hexagon with two hexiamonds, allowing isolated moniamond holes. |
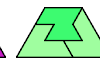 | Heptiamond Pair Trapezia / Trapezoids. With copies of two given heptiamonds, make the smallest trapezium (or trapezoid). |
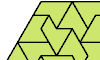 | Minimal Convex Polyiamond Tilings. With copies of a given polyiamond make the smallest convex polyiamond. |
 | Convex Polygons from Pairs of Polyiamonds. With copies of two given polyiamonds make the smallest convex polyiamond. |
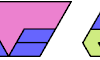 | Convex Polygons from Pairs of Scaled Polyiamonds. With as few scaled copies of two given polyiamonds as possible, using at least one of each, make a convex polyiamond. |
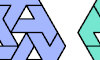 | Polyiamond Convexification with Holes. Arrange copies of a given polyiamond to form a convex polyiamond with single-cell holes in it. |
 | Convex Shapes from Isolated Hexiamond Pairs. Arrange copies of a two hexiamonds to form a convex polyiamond without letting copies of one of the hexiamonds touch. |
 | Convexification Numbers for Polyiamonds. Pack copies of a polyiamond into some convex polyiamond, leaving as few cells vacant as possible. |
 | Convex Polygons from the 12 Hexiamonds. Arrange the 12 hexiamonds to form a convex polyiamond. |
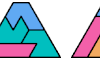 | Convex Polygons from Three Hexiamonds. With copies of three given hexiamonds make the smallest convex polyiamond. |
 | Similar Polyiamonds Forming a Convex Shape. Arrange scaled copies of a polyiamond to make a convex polyiamond. |
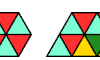 | Tiling a Convex Shape with a Polyming. Arrange copies of a polyming to form a minimally convex shape. |
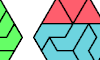 | Tiling a Badge with Two Polyiamonds. Arrange copies of two polyiamonds to form a polyiamond badge. |
 | Two-Hexiamond Balanced Parallelograms. Tile a parallelogram with two hexiamonds in equal quantities. |
 | Polyiamond Tilings With Few Sides. Arrange copies of a polyiamond to form a polygon with as few sides as possible. |
 | Tiling a Polyiamond with Scaled Q Pentiamonds. Arrange copies of the Q pentiamond at various scales to form a given polyiamond. |
 | Tiling a Polyiamond with Scaled J and Q Pentiamonds. Arrange copies of the J and Q pentiamonds at various scales to form a given polyiamond. |
 | Tiling a Polyiamond at Scale 2 with Two Hexiamonds. Arrange copies of two hexiamonds to form some polyiamond that has been scaled up by a factor of 2. |
 | Hexiamond Triplets. Arrange the 12 hexiamonds to form three congruent polyiamonds. |
 | Yin-Yang Diamonds. Arrange the 12 hexiamonds to cover a bi-colored diamond. |
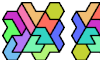 | Tiling a Polyhex with the 12 Hexiamonds. Arrange the 12 hexiamonds to form a polyhex. |
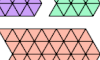 | Similar Hexiamond Figures, 2–2–8. With the 12 hexiamonds, make three similar figures, one at double scale. |
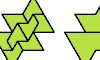 | Polyiamond Bireptiles. Join two copies of a polyiamond, then dissect the result into equal smaller copies of it. |
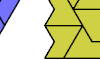 | Uniform Polyiamond Stacks. Arrange copies of a polyiamond to form a shape with equal, contiguous rows of cells with even length. |
 | Containing Pairs of Hexiamonds. Find the smallest polyiamonds that can contain every pair of distinct hexiamonds. |
 | Polyiamond Irreptiling. Dissect a polyiamond into smaller copies of itself, not necessarily the same size. |
 | Polyming Irreptiling. Dissect a polyming into smaller copies of itself, not necessarily the same size. |
 | Scaled Polyiamond Tetrads. Arrange four copies of a polyiamond at varying scales so that each borders the others. |
 | Tiling a Shape with Ternary Symmetry with the Heptiamonds and the Tetrahexes. Tile a shape with 3-fold symmetry with all 24 heptiamonds, then with all 7 tetrahexes. |
 | The Lobster and the Snake. Four puzzles about the Lobster and Snake hexiamonds. |