In issue 14 of Rodolfo M. Kurchan's Puzzle Fun, Gustavo Piñeiro defines the rectification number of a polyomino as the least number of cells that can be left vacant when copies of the polyomino are packed in a rectangle.
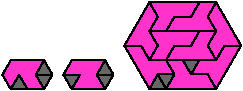
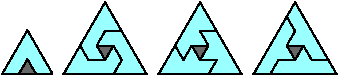
Polyiamonds cannot form rectangles. Here I investigate the problem of packing copies of a polyiamond into some convex polyiamond, leaving as few cells as possible vacant.
In the results below, I omit polyiamonds that can tile some convex polyiamond without adding moniamonds. Such polyiamonds have Convexification Number 0.




















Last revised 2023-09-09.