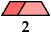
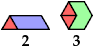
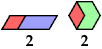
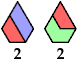
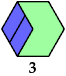
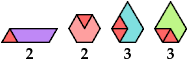
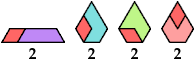
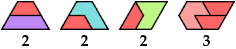
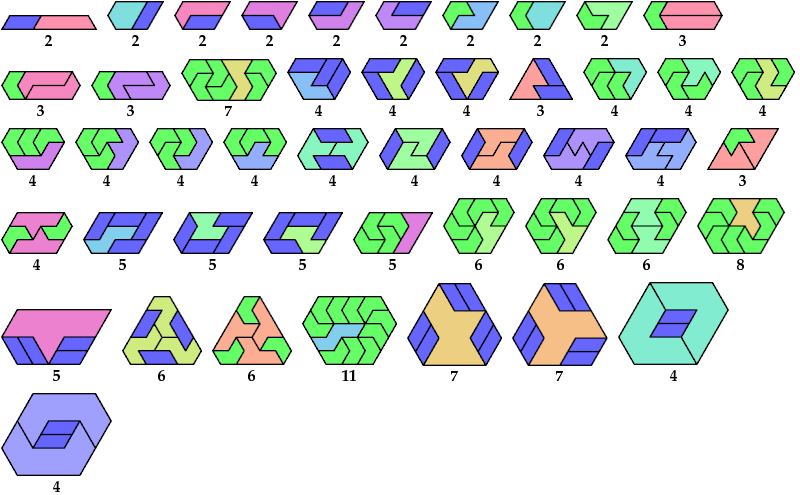
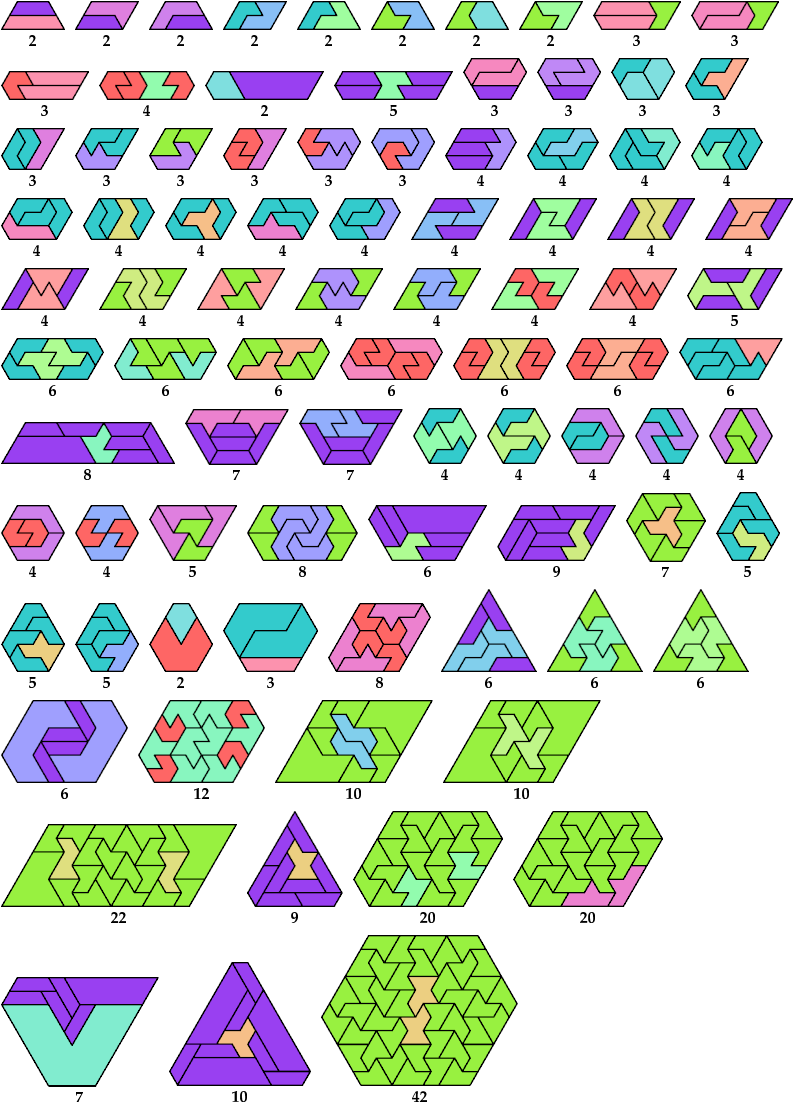
Here I show minimal known convex polygons formed by pairs of scaled polyiamonds with 1 through 7 cells. If you find a smaller solution or solve an unsolved case, please write.
Carl Schwenke and Johann Schwenke found many new and improved solutions.
See also Convex Polygons from Pairs of Polyiamonds.
| Cells | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| 2 | @ | ||||||
| 3 | @ | @ | |||||
| 4 | @ | @ | @ | @ | |||
| 5 | @ | @ | @ | @ | @ | ||
| 6 | @ | @ | @ | @ | @ | > | |
| 7 | @ | @ | @ | @ | @ | > | > |







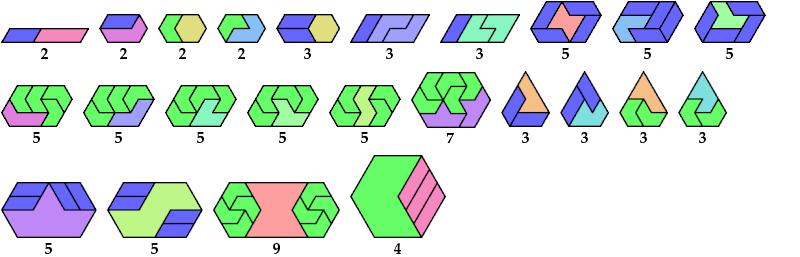
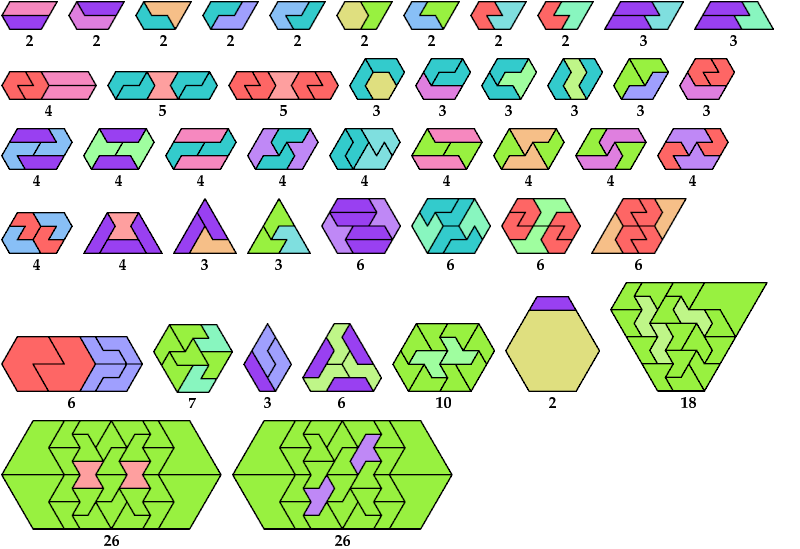

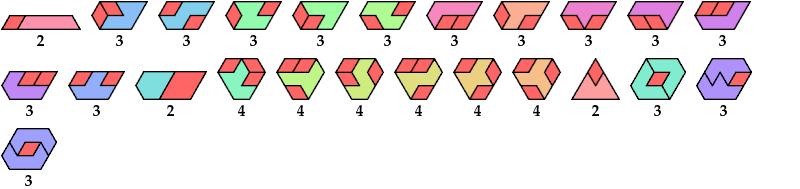
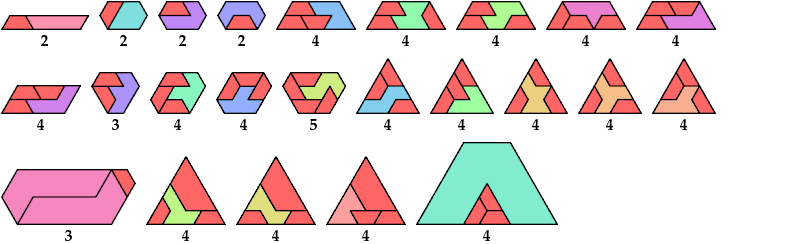
Last revised 2025-11-03.