 |
 |
 |
 |
 |
 |
Introduction |
A brief introduction to order-13 and it's 38 quadrant magic arrays. |
Ex. 1 - 1 way quadrant magic |
This pandiagonal magic square contains four p34 magic arrays. |
Ex. 2 - 3 way quadrant magic |
This pandiagonal square contains four each of p05, p13 and p38 arrays. |
Ex. 3 - 4 way quadrant magic |
This pandiagonal square has four each of p02, p09, p21 and p25 arrays.. |
Ex. 4 - 6 way quadrant magic |
This pandiagonal contains sets of p05, p12, p14, p18, p27 and p32. |
Ex. 5 - 10 way quadrant magic |
This pandiagonal has p02, p03, p09, p10, p15, p16, p21, p25, p26 and p30. |
Ex. 6 - 10 way quadrant magic |
This pandiagonal has p01, p03, p05, p08, p11, p14, p19, p22, p24 and p33. |
Ex. 7 - 10 way quadrant magic |
This pandiagonal has p01, p08, p09, p17, p18, p21, p22, p30, p32and p37. |
Ex. 8 - 10 way quadrant magic |
This pandiagonal has p01, p04, p05, p09, p12, p16, p17, p20, p28 and p32. |
Ex. 9 - 11 way quadrant magic |
This one has p02, p04, p05, p07, p15, p18, p21, p23, p 26, p36 and p37. |
Ex. 10 - 14 way quadrant magic |
p01, p02, p04, p05,p07, p09, p21, p23, p24, p25,p33, p35, p36 and p37. |
Conclusions & Questions |
Conclusions reached and suggestions for further study. |
![]()
My Quadrant Magic Squares page contains general information on this subject. It also covers orders 5 and 9.
Order-13 seems to be very rich in quadrant magic squares, especially squares that are
quadrant magic in multiple ways.
Following are examples that range from 1-way quadrant magic to 14-way quadrant magic.
I found these by iterating through Aale de Winkel's order-13 Latin Prescriptions. This method only generates a sub-set of all the possible order-13 magic squares. I leave the use of alternate search algorithms as an exercise for others.
Following are the 38 magic arrays for order-13. They are presented in the order and with the index number de Winkel assigned them. I have included the names of the original five patterns found and investigated.
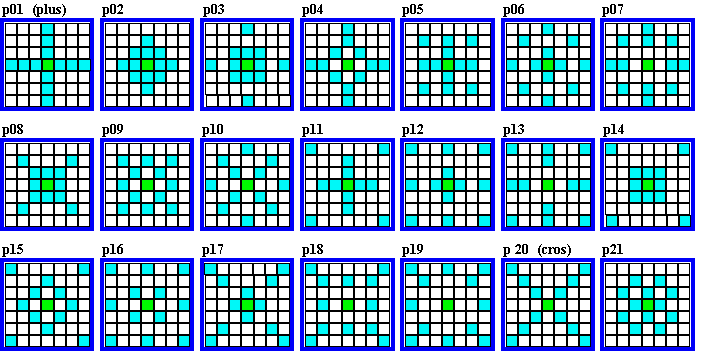
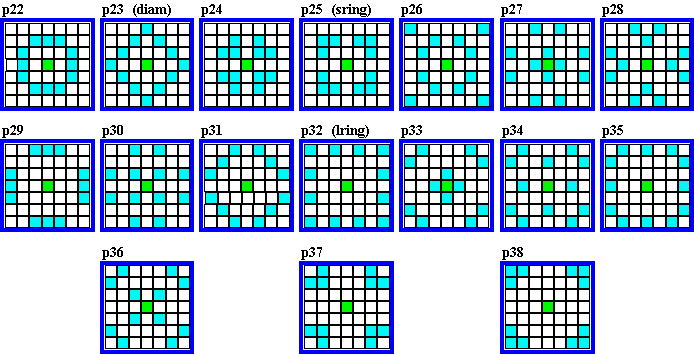
Remember, to be quadrant magic, a magic square must have 4 identical
arrays in the 4 quadrants.
The plusmagic (p01), and diammagic (p23), quadrant magic squares are the only types that
can transform into an order-13
(or any order 8m - 3) isolike magic star.
30 of the 38 arrays have cells that are in common with the orthogonal adjacent arrays.
This is because the center row of the magic square is common to the two top and bottom
arrays.. Likewise,with the center column, which is common to the two side-by-side arrays.
Examples: On this page I will present 10 example quadrant magic squares. All but the first example are multiple-way quadrant magic. This means that the same magic square has multiple sets of 4 magic arrays in it's four quadrants.
The table following shows which magic arrays are shown in each example, and which are
present as a set of 4, but not shown.
In almost all cases, I show only one of a particular magic array, but each is one of a set
of 4, inhabiting all 4 quadrants of the magic square.
I shows the latin prescription for each square displayed, but in abbreviated form. The
parentheses are left off, as is the final digit of each vector (which is always 0 if
dealing with only 2 dimensions).
The last row (extra) shows the total number of different magic arrays that are present at
least once in the square, and the number in the most populated quadrant.
My choice of examples provides for the display of a good variety of quadrant
magic arrays The only ones not shown are p06 and p31 for which I have not yet found
quadrant magic squares for, and p29 which I could not find in suitable combination with
other sets of 4 arrays.
A p29 quadrant magic square is (1, 3, 0)(3, 1, 0). It is also p5, 13, 15, 30 and 38
quadrant magic.
| The sets of 4 identical arrays that occupy the 4 quadrants of the example quadrant magic squares | ||||||||||
| P # | 1-way 1,2-1,3 |
3-way 8,6-8,7 |
4-way 5,1-5,11 |
6-way 3,9-9,3 |
10-way 1,5-1,8 |
10-way 5,7-7,5 |
10-way 5,9-9,5 |
10-way 10,5-5,10 |
11-way 4,12-9,12 |
14-way 5,11-11,5 |
| 1 | X | X | X | @ | ||||||
| 2 | @ | X | X | X | ||||||
| 3 | X | @ | ||||||||
| 4 | X | X | @ | |||||||
| 5 | @ | X | X | @ | X | X | ||||
| 6 | ||||||||||
| 7 | @ | X | ||||||||
| 8 | X | @ | ||||||||
| 9 | @ | X | X | X | X | |||||
| 10 | @ | |||||||||
| 11 | @ | |||||||||
| 12 | @ | X | ||||||||
| 13 | @ | |||||||||
| 14 | @ | X | ||||||||
| 15 | @ | X | ||||||||
| 16 | X | @ | ||||||||
| 17 | @ | X | ||||||||
| 18 | @ | X | X | |||||||
| 19 | @ | |||||||||
| 20 | @ | |||||||||
| 21 | @ | X | X | X | X | |||||
| 22 | X | @ | ||||||||
| 23 | @ | X | ||||||||
| 24 | X | @ | ||||||||
| 25 | @ | X | X | |||||||
| 26 | @ | X | ||||||||
| 27 | @ | |||||||||
| 28 | @ | |||||||||
| 29 | ||||||||||
| 30 | @ | X | ||||||||
| 31 | ||||||||||
| 32 | X | @ | X | |||||||
| 33 | @ | X | ||||||||
| 34 | @ | |||||||||
| 35 | @ | |||||||||
| 36 | @ | X | ||||||||
| 37 | X | @ | X | |||||||
| 38 | @ | |||||||||
| extra | 24/20 u.l. | 26/22 u.r. | 25/19 u.r. | 26/19 l.l. | 28/19 l.r. | 35/31 u.l. | 24/17 u.l. | 36/ 25 l.l. | 32/32 u.l. | 32/32 u.l. |
| @ | = 4 patterns of this present and at least 1 shown |
X | = 4 copies of this present but not shown | |||||||
The last row (extra) shows the total number of different magic arrays that are present at least once in the square, and the number in the most populated quadrant. (u.l. = upper left quadrant, l.l. = lower left, etc.)
Notice that the 2 examples with the most magic arrays are both 10-way quadrant magic (not 11 or 14-way).
![]()
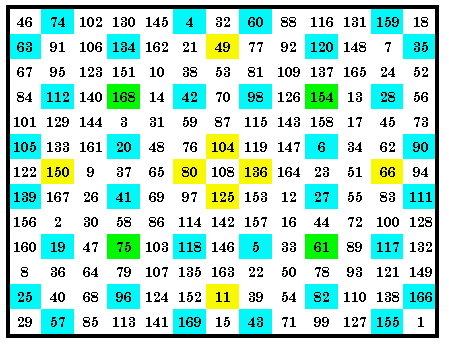 |
This quadrant magic square contains 1 set of 4 of the p34 magic arrays in
it’s 4 quadrants. Therefore it is a p34 quadrant magic square. However, a total of 24 different magic arrays each appear in the square at least once, with 20 in the top left quadrant. The green cells are the center cells of each quadrant. They are included as 1 of the 13 cells of each magic array in that quadrant. Notice that cells in the central row and central column (shown here in yellow) are common to two adjacent arrays. This is Latin prescription (LP) (1,2,0) (1,3,0). |
![]()
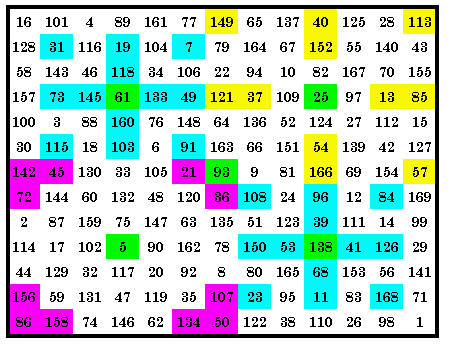 |
This quadrant magic square contains 3 sets of 4 p05 (shown twice), p13 and
p38 magic arrays in it’s 4 quadrants. Therefore it is a 3-way quadrant magic square. However, a total of 26 different magic arrays each appear in the square at least once, with 22 in the top right quadrant. The green cells are the center cells of each quadrant. They are included as 1 of the 13 cells of each magic array in that quadrant. As usual, all cells in the central row and central column are common to orthogonal
adjacent arrays. LP is (8, 6, 0)(8, 7, 0) |
 |
This quadrant magic square contains 4 sets of 4 magic arrays in it’s
4 quadrants. The p02, p09, p21 and p25, making it a 4-way quadrant magic square. Of the 8 patterns (out of 38) that have no cells on the outside rows or columns of the quadrant, 4 of them are in this square. However, a total of 25 different magic arrays each appear in the square at least once, with 19 in the top right quadrant. The green cells are the center cells of each quadrant. They are included as 1 of the 13 cells of each magic array in that quadrant. The LP is (5, 1, 0)(5, 11, 0) |
![]()
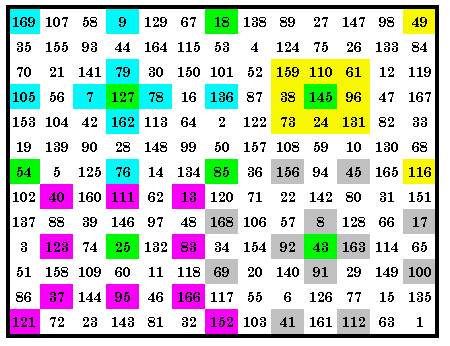 |
This quadrant magic square contains sets of four p12, p14, p18 and p27
magic arrays in it’s 4 quadrants. Also present but not shown here are sets of four
p05 and p 32. Therefore it is a 6-way quadrant magic square. However, a total of 26 different magic arrays each appear in the square at least once, with 19 in the lower left quadrant. The green cells are the center cells of each quadrant. They are included as 1 of the 13 cells of each magic array in that quadrant. As usual, all cells in the central row and central column are common to orthogonal adjacent arrays. As usual, I use green to show common cells in this diagram. The LP is (3, 9, 0)(9, 3, 0) |

 |
This quadrant magic square contains sets of 4 p10, p15, p26 and p30 magic
arrays in it’s 4 quadrants. Also present but not shown here are sets of 4 p02, p03,
p09, p16, p21 and p25. Therefore it is a 10-way quadrant magic square. A total of 28 different magic arrays each appear in the square at least once, with 19 in the lower right quadrant. The green cells are the center cells of each quadrant. They are included as 1 of the 13 cells of each magic array in that quadrant. As usual, all cells in the central row and central column are common to orthogonal adjacent arrays and as usual, I use green to show the 1 common cell in this diagram. The LP is (1, 5, 0)(1, 8, 0). |
![]()
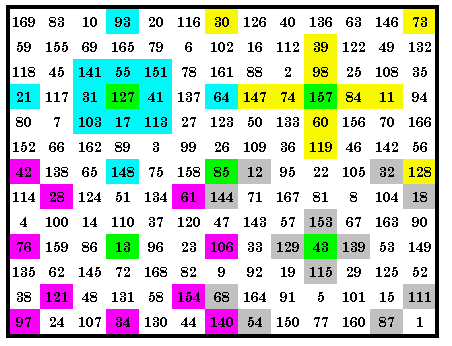 |
This quadrant magic square contains sets of 4 p03, p11, p19 and p33 magic
arrays in it’s 4 quadrants. Also present but not shown here are sets of 4 p01, p05,
p08, p14, p22 and p24. Therefore it is a 10-way quadrant magic square. A total of 35 different magic arrays each appear in the square at least once, with 31 in the upper right quadrant. The green cells are the center cells of each quadrant. They are included as 1 of the 13 cells of each magic array in that quadrant. As usual, all cells in the central row and central column are common to orthogonal adjacent arrays and as usual, I use green to show the 1 common cell in this diagram. The LP is (5, 7, 0)(7, 5, 0). |
![]()
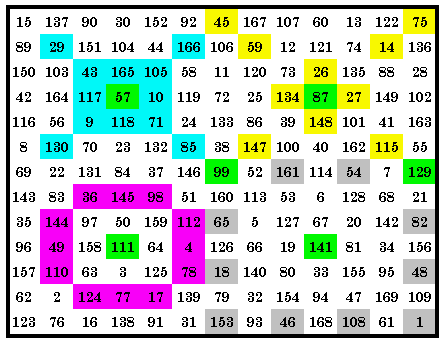 |
This quadrant magic square contains sets of 4 p08, p17,p22 and p32 magic
arrays in it’s 4 quadrants. Also present but not shown here are sets of 4 p01, p09,
p18, p21, p30 and p37. Therefore it is a 10-way quadrant magic square. A total of 24 different magic arrays each appear in the square at least once, with 17 in the upper left quadrant. The green cells are the center cells of each quadrant. They are included as 1 of the 13 cells of each magic array in that quadrant. The green 99 and 129 are common to the 2 right hand arrays. The LP is (5, 9, 0)(9, 5, 0). |
![]()
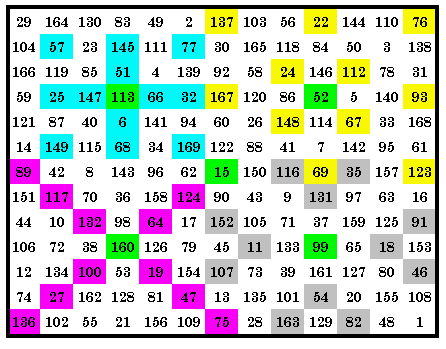 |
This quadrant magic square contains sets of 4 p05, p16, p20 and p28 magic
arrays in it’s 4 quadrants. Also present but not shown here are sets of 4 p01, p04,
p09, p12, p17 and p32. Therefore it is a 10-way quadrant magic square. 36 of the 38 magic arrays each appear in the square at least once, with 25 in the lower left quadrant. The green cells are the center cells of each quadrant. They are included as 1 of the 13
cells of each magic array in that quadrant. The LP is (5, 10, 0)(10, 5, 0). |
![]()
 |
This quadrant magic square contains sets of 4 p07, p23, p36 and p37 magic
arrays in it’s 4 quadrants. Also present but not shown here are sets of 4 p02, p04,
p05, p15, p18, p21 and p26. Therefore it is an 11-way quadrant magic square. Be aware that I have displayed these patterns out of order to avoid overlapping cells. 32 magic arrays each appear in the square at least once, with all 32 in the upper left and upper right quadrants. The green cells are the center cells of each quadrant. They are included as 1 of the 13
cells of each magic array in that quadrant. |
![]()
 |
This quadrant magic square contains sets of 4 p01, p04, p24 and p35 magic
arrays in it’s 4 quadrants. Also present but not shown here are sets of 4 p02, p05,
p07, p09, p21, p23, p25, p33, p36 and p37. Therefore it is a 14-way quadrant magic square. 32 magic arrays each appear in the square at least once, with all 32 in the upper left quadrant. The green cells are the center cells of each quadrant. They are included as 1 of the 13
cells of each magic array in that quadrant. |
![]()
![]()
For order 13 there are a total of 262,596,783,764 combinations of 13 cells in the
quadrant total of 49 cells.
This number is reduced to 38 patterns when we apply the restrictions that the pattern be
fully symmetric around the central cell of the quadrant. We call these 38 arrangements of
13 cells, quadrant magic arrays (Q. M. A.).
They are identified with the numbers p01 to p38.
A quadrant magic square is any magic square that contains a set of 4 identical Q. M. A. in
its four quadrants.
Many quadrant magic squares contain multiple sets of four identical Q. M. A.
All order-13 quadrant magic squares found so far are pandiagonal (although a
number of order-5 and order-17 quadrant magic squares found were not
pandiagonal).
Are there any regular (not pandiagonal) quadrant magic squares of order-13?
I have not yet found any order-13 p06 or p31 quadrant magic squares.
Are there any such squares?
Are there any quadrant magic squares that are greater then 14-way quadrant magic?
I displayed a magic square containing 35 and another with 36 Q. M. A.
Are there any quadrant magic squares that contain at least one of
all 38 Q. M. A?
![]()
Return to Quadrant M.S., Home, Order-17 Q.M.S. Please send me Feedback about my Web site!
Harvey Heinz harveyheinz@shaw.ca
This page last updated
December 22, 2003
Copyright © 1999 by Harvey D. Heinz