A polycube is a set of unit cubes joined in such a way that each face of the cube is either completely joined to another or completely free of any join.
Note: In the polycube diagrams a dot represents a continuation upwards, a circle downwards and a dot in a circle shows continuation in both directions.
There are eight tetracubes (see below).
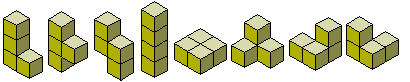
Two boxes can be constructed with this set.
Notice that the first five pieces are solid versions of the tetrominoes while the remaining three are truly three-dimensional. In listing the higher order polycubes the pieces made from the corresponding polyominoes will not be shown. Note also that the last two pieces are mirror images of each other. Unlike the polyominoes where we have a third dimension in which to turn a piece over, we cannot flip our polycubes in a fourth dimension so we generally consider mirror pairs a distinct although this is a choice we need not make.
Although a number of constructions are possible with the tetracubes the limited number of pieces restricts the design possibilities and it is only when we get to the pentacubes that we can really let our creativity loose.
The six tetracubes which are not rectangular blocks (the first three and last three above) together with the one tricube which is not a block have a total volume of 27 unit cubes and are the basis of the Soma Cube. Below are a number of links to Soma Cube sites some of which have references to polycubes etc. -
Soma Cube Central Puzzles: Soma Cube The Soma Cube Puzzle - 1 Soma Puzzles Soma Cube Construction The Soma Cube Soma Cube Piece Assembly Thorleif's SOMA page Soma Applet
There are 29 pentacubes consisting of solid versions of the 12 pentominoes together with the 17 other solids shown below. There is no generally agreed notation for the 29 pentacubes but two schemes have been used. Also Kate Jones of Kadon Enterprises has produced a different naming convention for various polycube sets which can be seen at the links below
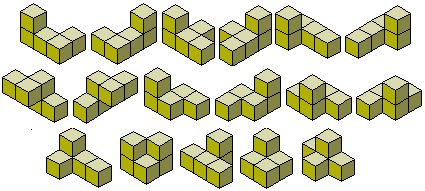
Below are some constructions which can be made with the full set of pentacubes.
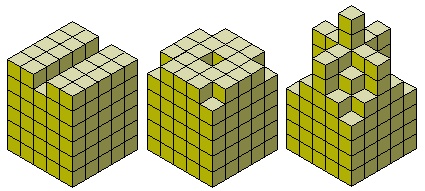
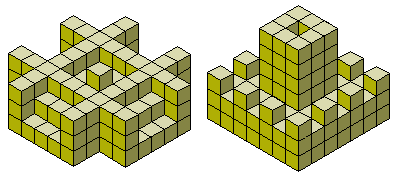
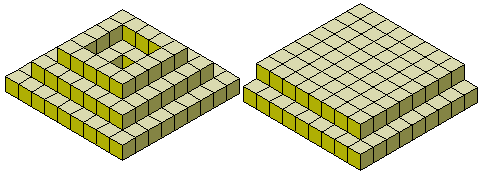
One problem for the pentacubes is to create a cylinder 7 units high with a cross section in the shape of a duplicated pentomino. This requires only 28 pieces and so the solid pentomino corresponding to the cross section is to be omitted. All 12 cases are possible and one example, the T, is shown here.

We can also look for a pentacube construction with the maximum number of internal holes. Solutions are shown her for both the solid pentominoes and the pentacubes.

Bruno Gilleta has a number of pages on pentacubes including java animations of the construction of a 3x4x5 and 2x5x6 boxes with the 12 solid pentominoes. Also for those interested in further pentacube constructions see the Pentacube Contest site.
The pentacubes are the first set of polycubes where we could find other pieces if we were not restricted to three dimensions. If we were to look at four-dimensional pentacubes then we should ignore mirror pairs and add four more pieces. This would give the 12 planar pieces plus the 15 below. The four-dimensional pieces have a green cube where another cube is added in the extra dimension. Note that we have one four-dimensional mirror pair.
This would give a total of 27 pieces which form the 3x3x3x5 hyperbox below.
Note that we have one four-dimensional mirror pair and in higher dimensions there would be only 26 pieces.
There are 166 hexacubes consisting of solid versions of the 35 hexominoes together with a further 131 pieces.
The total volume of the 166 hexacubes is 996 and a number of rectangular boxes can be made with the full set. Since there are pieces which cover 3 cubes in two perpendicular directions the only possible boxes to be made with the full set are 2x3x166, 2x6x83 and 3x4x83. If we use only one of each mirror pair then we are left with 112 pieces which will make 2x3x112, 2x6x56 and 3x4x56 boxes (see diagrams).
Below is another construction which can be made with all 166 pieces.

If you decide to make yourself a set or buy one from Kadon (it's the only place I know of where they are sold) then you may wonder how to start building a construction such as the one above. The best way is to do it upside down! If you make a frame in the shape of the hole you want to fill and then use the harder pieces first you will get to a situation where you are (hopefully) mostly using the hexominoes to fill the bottom layer.
Before trying something that complicated try making the boxes listed above or for an easier start just fit the hexacubes into a cube of side 10 with 4 gaps remaining. At first let the gaps be anywhere but then try placing them in a pattern such as shown below or make the four gaps into the shape of one of the tetracubes. With care you should be able to make a 9x10x10 block with 150 pieces and have the remaining 16 pieces all solid hexominoes so you can produce a number of different patterns without too much reorganisation.
Finally here are a few constructions made with the 35 solid hexominoes. No box is possible from the same colouring proof that applied to the planar hexominoes. The final construction contains the maximum number of internal holes which can be placed.
If we add an extra unbalanced piece to the set we can make a 6x6x6 cube. The construction below shows solutions for all eleven problems. The constructions at the top are formed with the eleven unbalanced pieces plus one duplication. These can be filled with the construction at the bottom made from the 23 remaining pieces.
There are 1023 heptacubes and if you want to see a drawing of the set I think you may have to produce it yourself! I don't know of anyone who has drawn let alone built the set but Patrick Hamlyn has used a computer to pack the heptacubes into thirty one 3x7x11 boxes.
Three German students have, however, constructed a set of heptacubes and produced classified lists. You can see their results here.
Physical constructions have been made, however, with the 108 heptacubes derived from the heptominoes. For details of boxes made with this set see the possible boxes listed by Mike Reid in Torsten Sillke's site or see diagrams of the solutions at Heptomino Packings. A better diagram of the solutions can be seen here.
Patrick Hamlyn has used a computer to find a way of making nine 3x4x7 boxes with this set.
Octacubes
No attempt will be made here to discuss the octacubes save to pose one problem. It is well known that a number of the hexominoes are nets of a cube and in a similar manner some octacubes will be the 'net' of a tesseract (four dimensional cube). One example is shown below and the problem posed here is to find which of the 6922 octacubes are nets of hypercubes. Martin Gardner posed this question in about 1984 and in 1966, Peter Turney counted 261 ways of unfolding the tesseract into an octacube.
Peter Esser has constructed a 8x9x41 box from the 369 solid octominoes. The green cubes in the diagram form the 1x8x8 block which is the only piece to cross from one layer to another.
Peter has now found another solution with the 1x8x8 block in the centre of each layer.