 |
 |
 |
 |
 |
Order-6 Characteristics |
Introduction and some facts about Order-6. |
| First solution solver's | A short history of the early solvers of magic
hexagrams. |
Adjacent Complement Pairs |
A table showing the complement pairs that are adjacent in the list of basic solutions.i.e. have consecutive index numbers. |
| Twenty Sets of four | Mr. Suzuki's groups, diagram of transformations & list. |
| Complements | Each solution has a complement, just like magic squares. |
| Super-Magic Stars | Six is the only order that can have the sum of peaks also magic. |
| Cell pairs equaling 13 | 6 pairs of cells define a way to put the 80 solutions into three groups. |
Definitions |
Review magic star definitions and general features. Use Back button to return |
| A Tribute to H. E. Dudeney | Applying all of Dudeney's findings to my solution list. |
Star-6 Basic Solutions, Sub-sets, Complements, |
All 80 basic solutions in index order, including complement #, how they fit in Mutsumi Suzuki's 20 sets of 4, H.E. Dudeney's classification and several other features. |
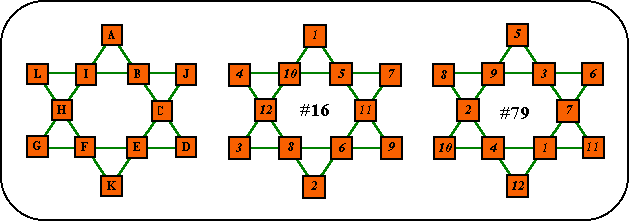
Order-6 is the lowest order pure magic star. It is also the only order (at least to order-12) that has more basic solutions then a higher order.The only exception is order-10a, which has more solutions then any of the four order-11patterns.
There is a total of 80 basic solutions consisting of 40 complement pairs.
The 80 solutions may be sub-divided into 20 sets of 4 solutions (Mutsumi Suzuki). They may
also be classified into three groups on the basis of which two or three pairs of cells sum
to 13 (Dudeney).
Each solution contains the consecutive series of integers from 1 to 12. The sum of this series is 78, there are 6 lines with each cell appearing in 2 lines, so the magic constant (S) is (2 x 78)/6 = 26.
It is also the only order star where there are solutions that have all the points summing to the magic constant. There are six such solutions, and by complementing, there are also six solutions with the valleys constant.
There can be no solutions with the points consisting of consecutive numbers because six consecutive numbers must always sum odd and all solutions have the points summing even. There are no solutions with the points all even or all odd.
Solution # 16, shown here, is the first of six super-magic stars, because the points also sum to 26. Solution # 79 is the last of six solutions where the valleys sum to 26.
Order-6 is the only magic star that does not have at least one continuous pattern. This pattern consists of two super-imposed triangles. (2 and 3 are the factors of 6). The sum of the large triangle points are always equal.
Each pattern contains 3 diamonds such as a, c, h, k whose points always sum to
26.
Each of the three opposite pairs of small triangles always sum to the same value.
There are 21 solutions where a + c = 13. In each case, and only these 21 cases, b + d, f + l and h + k also sum to 13. In addition, e + i and g + j also sum to 13, but these two pairs also sum to 13 in seven other solutions. See Cell pairs = 13.
In 1917, W. S. Andrews showed a magic hexagram using numbers 1 to 13, with no 10. [1]
In 1926,H. E. Dudeney
published 74 solutions for the magic hexagram using the consecutive numbers 1 to
12. He erroneously thought that was all there were. [2]
He discovered many interesting features of this smallest of the normal magic
stars. See my Dudeney page.
Martin Gardner reported in an Addendum to his 1965 article that E. J. Ulrlich, of Enid, Okla, USA, and A. Domergue of Paris, France, both discovered there are actually 80 solutions for the basic magic hexagram. However, he did not give dates for these discoveries. [3] I suggest that they were probably made between 1965 and 1975, because in the original column, Gardner mentions that there are 74 basic solutions and first mentions the 80 in the 1975 book!
Recently, while reviewing J.
R. Hendricks collection of notes, I found a reference to an early finding of all
80 solutions. [4]
John Hendricks recorded
“Mr.
(L. M.) Leeds wrote that he found all 80 basic magic hexagrams in 1932. More
recently, he computerized them and found no more.”
I expect that due to the short period after Dudeney’s publication, Mr. Leeds was probably the first to find all 80 solutions!
Laurance M. Leeds was a graduate of the School of Engineering 1934, Rutgers University in New Jersey, USA. He was inducted into their Hall of Fame posthumously in 2006 for his work on early television and radio.
In his unpublished book [4],
John Hendricks included a computer program he had written to find the 80
solutions.
As a point of interest, about 4 years later (1995, I also wrote a basic program
to find these 80 solutions. At that time I had still not located (seen)
any list of the 80 solutions.
[1] W. S. Andrews, Magic Squares and Cubes, Open
Court Publishing, 1917, page 342.
[2] H. E. Dudeney, Modern Puzzles, 1926. This book has been included in
it’s entirety in 536 Puzzles & Curious Problems Charles Scribner’s Sons, NY
1967 where this information appears in condensed form on pages 349-350.
[3 ] Martin Gardner,
Mathematical Recreations column of Scientific American, Dec. 1965,
reprinted with addendum in Martin Gardner, Mathematical Carnival, Alfred A.
Knoff, 1975
[4] J.R. Hendricks, The Aspiring Scientist, Unpublished, November, 1993,
page 10.
![]()
Solution numbers |
Pair # |
Remarks |
|
1 |
2 |
1 |
The first pair number and the first two solutions. |
5 |
6 |
4 |
Pair # 2 consists of solution 's 3 and 41 and pair # 3 consists of solutions 4 and 42. Solutions 7 and 32 are pair # 5. In general, the second solution of a pair are scattered throughout the list. |
11 |
12 |
9 |
|
32 |
33 |
28 |
The complement and pair partner for each solution
is shown in the Order-6 solution list. |
43 |
44 |
34 |
|
60 |
61 |
40 |
The last pair number consists of the last adjacent pair of solutions. |
 See the complete list of basic solutions for Order-6 here.Star-6
Basic Solutions,
See the complete list of basic solutions for Order-6 here.Star-6
Basic Solutions,
The set of basic solutions may be divided into twenty sets of four solutions each. These are shown in the table below, which also includes the index number from the master list.
Each of twenty basic solutions may be changed into three other solutions by the following transformations. These transformations will be equivalents and must then be normalized to a basic solution. The solution sets are identified by a number from 1 to 20, and the upper case letter A for the original with B, C and D indicating the 3 transformations.
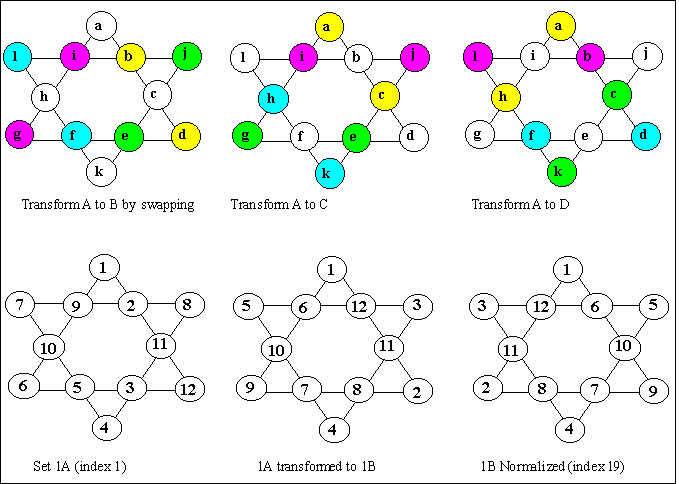
This feature was discovered by Mutsumi Suzuki and has appeared recently on the
WWW at
http://mathforum.com/te/exchange/hosted/suzuki/MagicStar.David.Prime.html.
Here of course, the solutions appear in my notation, i.e. line by line rather then row by
row.
Indx Main |-------- Basic Solutions (Upper case = peaks)-------| Index # of sub-set # Set A b c D e f G h i J K L B C D 1 1A 1 2 11 12 3 5 6 10 9 8 4 7 19 67 43 2 2A 1 2 11 12 4 3 7 8 10 5 6 9 27 74 44 3 3A 1 2 12 11 3 4 8 7 10 5 6 9 31 66 41 4 4A 1 2 12 11 4 5 6 10 9 7 3 8 20 75 42 5 5A 1 3 10 12 2 4 8 6 11 5 9 7 30 49 61 6 6A 1 3 10 12 2 7 5 9 11 8 6 4 13 53 60 7 7A 1 3 12 10 4 7 5 11 9 8 2 6 16 73 59 8 8A 1 4 10 11 5 3 7 6 12 2 9 8 24 79 58 9 9A 1 4 11 10 2 9 5 8 12 7 6 3 12 52 72 10 10A 1 4 12 9 5 2 10 7 8 3 6 11 39 78 50 11 11A 1 5 8 12 3 2 9 6 10 4 11 7 37 62 48 14 12A 1 5 11 9 3 2 12 6 7 4 8 10 38 65 45 15 13A 1 5 11 9 3 8 6 12 7 10 2 4 23 64 77 17 14A 1 5 12 8 2 6 10 4 11 3 9 7 34 54 71 18 15A 1 5 12 8 7 2 9 10 6 4 3 11 35 80 47 21 16A 1 6 11 8 2 7 9 4 12 3 10 5 33 56 69 22 17A 1 6 12 7 3 5 11 4 10 2 9 8 29 68 57 25 18A 1 7 8 10 2 3 11 5 9 4 12 6 40 46 63 26 19A 1 7 8 10 4 3 9 5 11 2 12 6 36 76 55 28 20A 1 7 10 8 3 6 9 4 12 2 11 5 32 70 51
As mentioned previously, all basic solutions have a complement. The complements are scattered throughout the list of solutions because the direct complement is an equivalent and must be normalized first, before it can be found in the list of basic solutions.
There are several coincidences worth noting.
The first two solutions on the list are a complement pair.
Index numbers 5 and 6, 11 and 12, 31 and 32, 43 and 44 and 60, 61 are the only other
adjacent pairs.
The corresponding pair numbers are 1, 4, 9, 28, 34, and 40.
The complements of solutions where the peaks are also magic have the valleys magic. Two of
these are adjacent, indices 38 and 39, with their complements, the magic valleys, 79 and
78 also adjacent.
NOTE that normally peak and valley values are not complements of each other.
I refer to magic stars with the peaks also magic as Super-Magic Stars. There are six of them as shown below , and their six complements have the valleys magic.
Solutions 38 and 39 are adjacent peaks.
Two adjacent valleys are solutions 66 and 67, while numbers 77, 78, and 79 are three
adjacent valleys!
Indx comp. a b c d e f g h i j k l Magic 16 73 1 5 11 9 6 8 3 12 10 7 2 4 peaks 23 77 1 6 12 7 4 10 5 11 9 8 2 3 peaks 27 67 1 7 8 10 9 5 2 11 12 3 6 4 peaks 31 66 1 8 7 10 9 5 2 12 11 4 6 3 peaks 38 79 1 9 11 5 4 10 7 6 12 3 8 2 peaks 39 78 1 9 12 4 3 11 8 7 10 5 6 2 peaks 66 31 3 4 8 11 1 2 12 5 6 7 10 9 valleys 67 27 3 4 8 11 2 1 12 6 5 7 9 10 valleys 73 16 4 2 8 12 3 1 10 5 7 6 9 11 valleys 77 23 5 1 9 11 3 2 10 4 7 6 8 12 valleys 78 39 5 2 10 9 1 4 12 3 6 7 8 11 valleys 79 38 5 3 7 11 1 4 10 2 9 6 12 8 valleys
It is again worth noting that order-6 is the only order that has solutions with the
peaks magic. For order-7 the first 7 consecutive numbers equal 28 instead of 30 while all
other consecutive sets are greater then 30.
With every order-n with n > 7, the number of first n consecutive
numbers is greater then the constant for that order.
All the magic peak solutions are type B of the 4 subsets of 20. Of the six
magic valleys, five are type C, the other is type D. Too bad!
Because the sum of the large triangle points are always equal, these sums will each be 13
when peaks are magic and 26 when valleys are magic.
![]()
The magic hexagram may be divided into six pairs of two cells and then classified into three groups on the basis of which pairs sum to 13. These pairs are: A + C, B + D, E + I, F + L, G + J, and H + K.
This classification is similar to Dudeney’s, but involves all six cells.
Group H-1 consists of 21 basic solutions with all 6 pairs summing to
13.
Group H-2 consists of 52 basic solutions with none of the six pairs
summing to 13.
Group H-3 consists of 7 basic solutions. Pairs E + I and G + J both sum to
13. The other 4 pairs do not sum to 13.
To put it another way:
if A + C = 13, then , B + D, F + L and H
+ K also = 13
if A + C ¹
13, then , B + D, F + L and H + K also ¹ 13
if E + I = 13 then G + J = 13: if E
+ I ¹ 13 then G + J ¹
13
if A + C = 13 and E + I = 13 then the
hexagram is Group H-1
if A + C ¹ 13
and E + I ¹ 13 then the hexagram is Group H-2
if A + C ¹ 13
and E + I = 13 then the hexagram is Group H-3
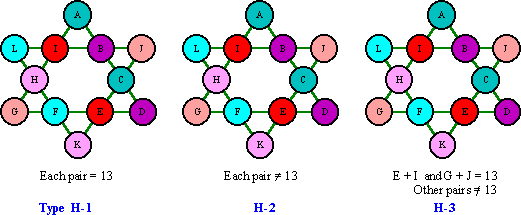
The 28 Dudeney class 1c solutions consist of the 21 type H-1 and the 7 type H-3 groups.
The group H-2 solutions are composed of all the other Dudeney classes.
Six of the seven H-3 solutions consist of three complement pairs.
![]()
Magic Star Definitions
The Order-6 List of Solutions.
A tribute to H. E. Dudeney
![]()

![]() Please send me Feedback about my Web site!
Please send me Feedback about my Web site!![]()

![]()
![]()
Harvey Heinz harveyheinz@shaw.ca
This page was first posted in April, 1998
This page last updated
June 25, 2009
Copyright © 1998, 1999 by Harvey D. Heinz