 |
 |
 |
 |
 |
|
|
to this page of 3-dimensional magic star patterns. New material will be added here as it becomes available and time permits. |
 |
An 8-point 3-D magic star |
Two interlocking triangle based pyramids. 12 lines of 3 numbers. |
A 10-point magic star 3-D magic star? |
Two interlocking square based pyramids. Magic? Impossible. |
The de Winkel 10 point magic star |
Is it a star? Anyway, it is magic! 16 lines of 3 numbers. |
Hermann Mierendorff's 3-D magic stars |
A 2003 paper expands on this type of magic star. |
![]()
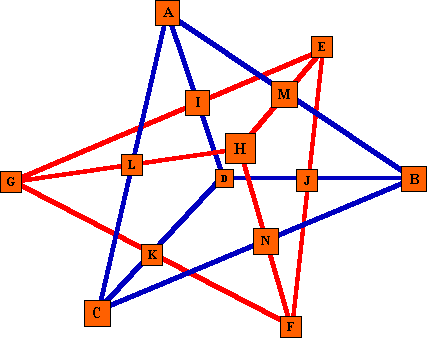 |
An 8-point 3-D magic starThis 3-dimensional 8-pointed magic star contains 12 lines with 3 numbers per line. It consists of two tetrahedrons (pyramids) each with six lines of three cells.The pyramids intersect at the midpoints of each of the 12 lines. Pyramid ABCD has D pointing away from the viewer. ABCD and EFGH each appear in three lines. |
The smallest possible series of numbers that can be arranged in this pattern to make each of the 12 lines sum to the same value is numbers 1 to 15 but without the 8. Because of parity, all the points must be odd and the midline values even or all the points even numbers and the midline values odd.
The equation for this pattern is 3(A+B+C+D+E+F+G+H) + 2(I+J+K+L+M+N) = 12S
However, the series from 1 to 15 produces only 7 correct lines and the series from 2 to 16 produces only 8 correct lines.
I sent Aale de Winkel the results of my search and a day or two later he e-mailed me the following solution which requires that 3 numbers must be left out of the series of consecutive numbers.
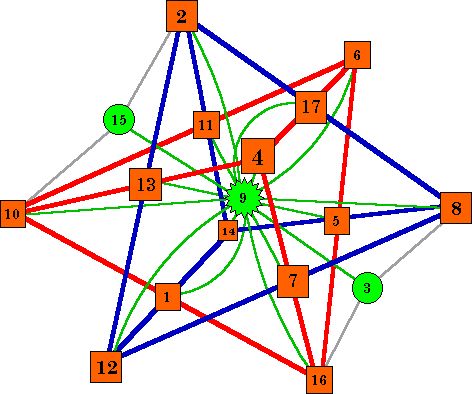 |
This solution, using the numbers from 1 to 17, but without the 3, 9 and
15, forms a magic 3-D star with 12 lines of 3 numbers all summing to 27. This is the only solution possible using this number set (not counting rotations or reflections). With different number sets, smaller possible magic constants are possible . See addendum at end. The three unused numbers 3, 9 and 15 (shown in green) may be incorporated in the
pattern as follows: Thus we have a pattern using the consecutive numbers from 1 to 17, forming 22 lines of 3 numbers, all summing to 27. |
Like all magic stars, there is a companion solution to this one. Subtract each number in the above solution from 18 to obtain the complementary solution.
 A
wooden block model of the 3_d magic star and |
 Here
all 17 numbers are used, producing a figure |
My special thanks to Aale de Winkel
for
helping me to visualize a 3-dimensional star as two intersecting tetrahedrons.
He also came up with the solution using the numbers 1 to 17 when my attempts using numbers
1 to 15 and 2 to 16 failed.
And, while I was busy putting this all together in a drawing, he realized that the 3
unused numbers (3, 9 and 15) could be incorporated as the star center and two satellites.
[1]
 [1]
Emails from Aale de Winkel April 5, 1999 and May16, 1999 ( and several
in-between)
[1]
Emails from Aale de Winkel April 5, 1999 and May16, 1999 ( and several
in-between)
![]()
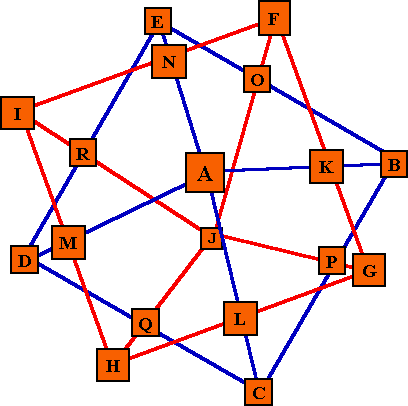 |
This is the cell name diagram for a 10-pointed magic star consisting
of two intersecting square-base pyramids. The blue pyramid has the tip pointing toward the viewer. The red pyramid has the tip pointing away. It is the same basic design as the triangle based star above and contains 18 numbers in 16 lines of 3 numbers each. The 10 point star would use 18 numbers from 1 to ? arranged in 16 lines of 3 numbers. It consists of 2 pentahedrons with the side midpoint cells of one being the base midpoint cells of the other one. In attempting to construct a 10 point star by copying features of the 8 point one, I finally realized there is a problem with parity, and all even point 3-D stars are probably impossible to construct using these features. |
Peak A and J are complements of each other.
Base corner B, C, D, E are complements of base corners F, G, H, I.
Midpoint cells of the base are complements of midpoint cells of the vertical sides.
All point cells are even, with the midpoint cells odd, or vice versa.
Magic Sum (S) equation is 4(A+J)+3(B+C+D+E+F+G+H+I)+2(K+L+M+N+O+P+Q+R)= 16S
BT using complement pair totals (and assuming we are using the series from 1 to 27) this
simplifies to
4(1x28)+3(4x28)+2(4x28) = 16S, so in this case S=42
However, each line (in this case) has two even and one odd number, requiring an odd magic
sum.
Sets of 5 even numbers with their complements, 5 different numbers, are only found in
number ranges from 1 to 27, 1 to 31, 1 to 35, etc. In each case, the resulting magic sum
is even., when it is required to be odd.
Sets of 5 odd numbers with their complements, 5 different numbers, are only found in
number ranges from 1 to 29, 1 to 33, 1 to 37, etc. In each case, the resulting magic sum
is odd., when it is required to be even.
I was starting to look for solutions using all even or all odd numbers only, when I
received the following impossibility proof from
Hermann Mierendorff. [2]
Hermann Mierendorff's impossibility proof
Let the values of the 10-point star be A,B,...,R.
We consider the following sums of values which lay on a line:
s1:=A+K+B, s2:=B+P+C, s3:=C+Q+D, s4:=D+M+A,
s5:=F+K+G, s6:=G+P+J, s7:=J+Q+H, s8:=H+M+I.
Let all the values on a line sum up to the magic number m.
This means s1=s2=s3=s4=s5=s6=s7=s8=m.
Hence -s1+s2-s3+s4+s5-s6+s7-s8=0.
On the other hand, we see easily
-s1+s2-s3+s4+s5-s6+s7-s8=F-I.
Hence F-I=0, i.e. F=I.
Therefore, at least F and I are identical, i.e. there is no magic star of this kind.
The same proof also works for all 3D stars which are build up using two n-sided pyramids as soon as n>3 (hh).
[2] Hermann Mierendorff email of Dec. 4, 2000 (His first email on this subject was Aug. 9, 2000)
![]()
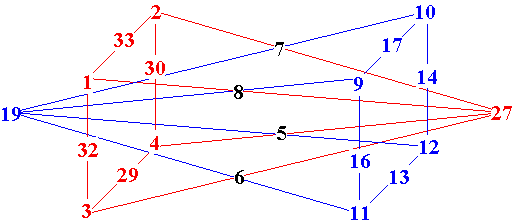
This magic object may not look much like a star, but it is magic! It
consists of two square based triangles with the midpoints of the vertical sides sharing
common numbers.
It uses 22 of the numbers from 1 to 33 to form 16 lines of 3 numbers. Each line sums to
36.
Aale de Winkel has discovered (about March, 2001) 3 other similar magic stars with sums of
42, 66 and 78.
See them and other magic objects at his
Magic Encyclopedia site.
In an above section on this page, Hermann Mierendorff gives an impossibility proof for a 10 pointed magic star of the style of the 3-D star shown.
In a paper published in 2003 [1], Mierendorff used pyramids and prismoids (or truncated pyramids) for building the polyhedra, the intersection of which forms the stars he was investigating. He found there are many magic stars consisting of two interconnected trumcated pyramids (he calls these twin body stars), if one restriction is applied.
Consider the number of sides in the base of the pyramid to be the width (w), and the number of layers when moving from 1 point to the diametrically opposite point the height (h). For example, the 3-D 8 point magic star above has w = 3 and h = 4; the 10 point non-magic star has w = 4 and h = 4. De Winkelís 10 point star has w = 4 and h = 5 and is magic.
The paper shows that magic star labelling exists for any star (w,h) if and only if h = w + 1. The following information is condensed from the cited paper with the authorís consent.
Some solutions for magic stars (w,h) of 3,4.
|
|
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
|
|
p, q |
|
1 |
2 |
8 |
12 |
14 |
6 |
16 |
10 |
4 |
11 |
5 |
1 |
13 |
17 |
7 |
1-17, no 3,9,15. |
S = 27 |
18, 18 |
|
2 |
1 |
4 |
6 |
7 |
3 |
8 |
5 |
2 |
14 |
11 |
9 |
15 |
17 |
12 |
1-17, no 10,13,16. |
S = 22 |
9, 26 |
|
3 |
10 |
13 |
15 |
16 |
12 |
17 |
14 |
11 |
6 |
3 |
1 |
7 |
9 |
4 |
1-17, no 2,5,8. |
S = 32 |
27, 10 |
|
4 |
1 |
9 |
10 |
12 |
6 |
15 |
7 |
4 |
11 |
3 |
2 |
13 |
14 |
5 |
1-15, no 8. |
S = 24 |
16, 16 |
Solution 1 is the one shown on this web page. I consider it the prettiest because all point values are even numbers and all crossings (valleys) are odd numbers. Mierendorff calls this feature perfectly shuffled. As previously mentioned on this page, all solutions can generate a complementary solution simply by subtracting each number from the maximum number in the range plus 1. The other 3 solutions are other possibilities for the 8 point star
Another feature that is important in the analysis of this type of magic figure is the sum of opposite point values. Similarly the sum of opposite cross values. He designates them respectively as p and q. 2p+q=S, so q is obviously always even. This result has been proven and it was one of the reasons to introduce p and q.
In the above table, the arbitrarily labelled points are A to H, with the valleys labelled I to N. Comparing these with the first diagram on the page we see that the opposite points are AF, BG, CE, and DH; opposite valleys are IN, JL, and KM.
| Mierendorff's paper incorporates what he calls a flat
representation to illustrate the magic lines of these stars without
resorting to complicated confusing diagrams of the stars.
The diagram above represents the star at the top of this page. The diagram below represents the 22 point star to the right.
|
 A 22 point
star of form 5,6. Each ring has 5 points, and there are 6 layers. 3 in each
of the two interlocking pyramids (polyhedra). |
The paper shows solutions for magic stars of this type for stars of 3,4 to 6,7.
[1] Hermann Mierendorff, Magic twin body stars
generated from chains of prismoids, Discrete Mathematics, 268 (2003) 315-323.
(Although I was advised of this paper, I did not actually see it until 2009.)
Please send me Feedback about my Web
site!![]()
![]()

![]()
Harvey Heinz harveyheinz@shaw.ca
this page was originally posted May 25, 1999
This page last updated
April 03, 2009
Copyright © 1998, 1999, 2001 by Harvey D. Heinz