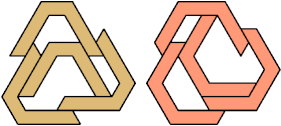Polyiamond and Polymar Tetrads
A tetrad is a plane figure made of four congruent shapes,
joined so that each shares a boundary with each.
Here I show various minimal tetrads for polyiamonds.
See also Scaled Polyiamond Tetrads.
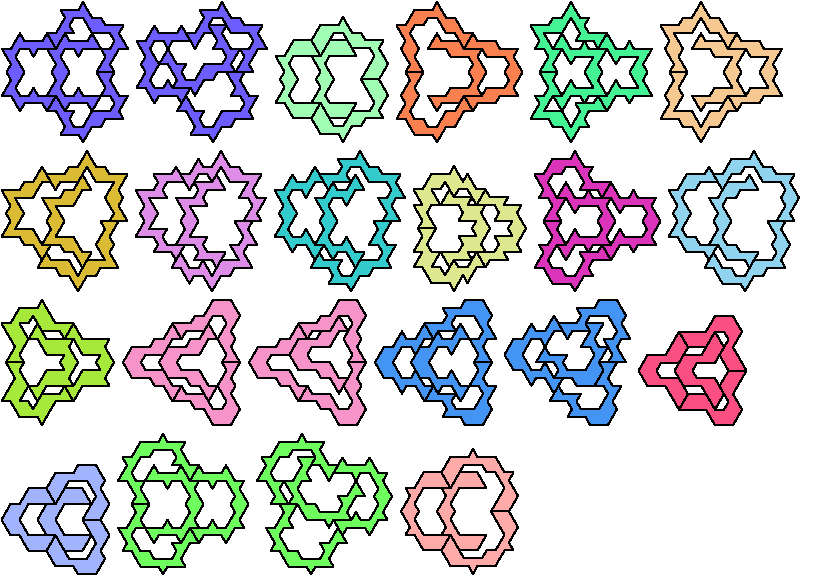
The smallest polyiamond tetrads use 10-iamonds.
According to Karl Scherer, Frank Rubin may have found the first solution.
The purple solutions were found by
Juris Čerņenoks.

Symmetric Tiles
The smallest tetrad made from a polyiamond with mirror symmetry
uses 12-iamonds:

It is also the smallest symmetric tetrad.
The smallest tetrad made from a polyiamond with birotary symmetry
uses 16-iamonds:
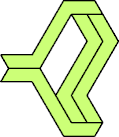
The smallest tetrads made from polyiamonds with horizontal mirror symmetry
use 17-iamonds:
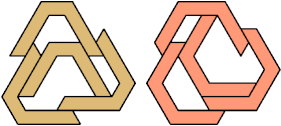
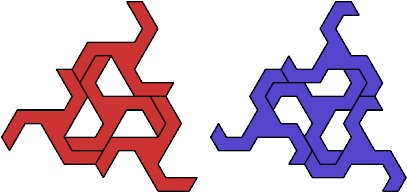
The smallest tetrad made from a polyiamond with ternary symmetry
uses 22-iamonds:
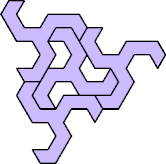
The smallest tetrads made from polyiamonds with ternary symmetry
about a vertex use 27-iamonds:
Restricted Motion
The smallest polyiamonds that form tetrads without being reflected
are these 10-iamonds:

They are also the smallest polyiamonds that form tetrads without
being rotated 60° or 180°.
Holeless
The smallest holeless tetrad made from a polyiamond
with mirror symmetry uses 22-iamonds.
It was found independently by Robert Ammann, Greg Frederickson, and
Jean L. Loyer.

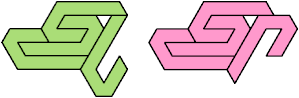
One-Cell Hole
The smallest tetrads with a single one-cell hole
are formed by this 16-iamond:
Two-Cell Hole
The smallest tetrad with a single two-cell hole
is formed by this 17-iamond:

Polymars
A polymar is a polyform formed by joining equilateral
triangles at edges and half edges.
The smallest polymars that can form tetrads are hexamars:

Symmetric Polymars
The smallest symmetric polymar that can form a tetrad
is this octamar:

Mirror-Symmetric Polymars
The smallest mirror-symmetric polymars that can form tetrads
are these decamars:
Last revised 2025-12-10.
Back to Polyform Tetrads
< Polyform Curiosities
Col. George Sicherman
[ HOME
| MAIL
]