where T(n) is the nth triangular number.
This formula implies that a square with side T(n)
might be dissected into 1 square of side 1, 2 squares of side 2,
and so on up to n squares of side n.
Such a tiling is a partridge tiling,
after the partridge in the song The Twelve Days of Christmas.
Robert Wainwright was the first to propose partridge tilings, and the first to find one: a square of side T(12), dissected in partridge fashion into squares with sides 1 through 12. Partridge tilings were later extended to shapes other than squares. See for example the August 2002 issue of Erich Friedman's Math Magic.
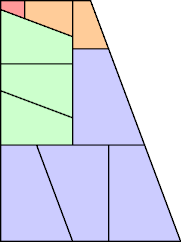
In 2020 I found this minimal partridge tiling of the monodom:
This is a contiguous partridge tiling. The tiles of each size form a connected group. This is the only contiguous partridge tiling of the monodom with 6 sizes (the minimum), except that any rectangle formed by two equal pieces may be flipped.
Joyce Michel has pointed out that the groups are connected in series: the 1 is adjacent to the 2's, the 2's to the 3's, and so on in a clockwise spiral.
Joyce also extended the above tiling to use 7 sizes:
This tiling also has the groups connected in series in a clockwise spiral.
The only other contiguous partridge tiling that I know of is Michael Reid's trapezoidal tiling with 4 sizes:

I have found no other contiguous partridge tiling of any plane figure, whether or not the tiling is minimal. If you find one, please write.
See also Contiguous Reverse Partridge Tilings.
Last revised 2023-07-13.