where T(n) is the nth triangular number.
This formula implies that a square with side T(n)
might be dissected into 1 square of side 1, 2 squares of side 2,
and so on up to n squares of side n.
Such a tiling is called a partridge tiling,
after the partridge in the song The Twelve Days of Christmas.
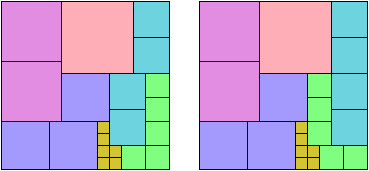
Robert Wainwright was the first to propose partridge tilings, and the first to find one: a square of side T(12), dissected in partridge fashion into squares with sides 1 through 12. Partridge tilings were later extended to shapes other than squares.
A reverse partridge tiling is a dissection in which the number of tiles decreases as the scale of the tile increases. For some values of n there is a number k such that
The first two values of n for which k is an integer are 6 (k=14) and 25 (k=195). Many polygons are known to have reverse partridge tilings for k=14, and a few for k=195. You can see them at Erich Friedman's Math Magic page for June 2007. They include solutions for the square, the equilateral triangle (and hence any triangle), the triamond, the L tetromino, and the monodrafter.
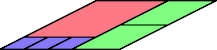
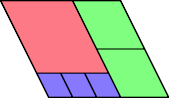
Here I show all known reverse partridge tilings with n=6 in which equal tiles are contiguous. According to Wainwright, this subproblem has apparently not been studied before. If you solve any cases not shown here, please write.

By transforming these solutions one may obtain a solution for any rectangle or parallelogram.
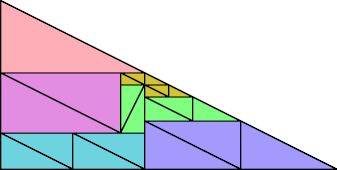
The smallest solution for the monotan, or monabolo, uses sizes 1 through 4 to make a monotan at scale 5√2. This format has no contiguous solutions. But with sizes 1 through 6 there are many solutions. Here is one:
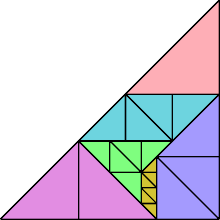
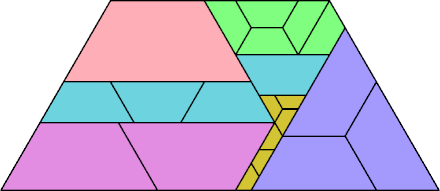
The right trapezoidal tritan also has many solutions.
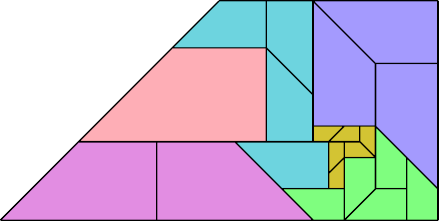
The parallelogrammatic ditan has a solution with n=4:

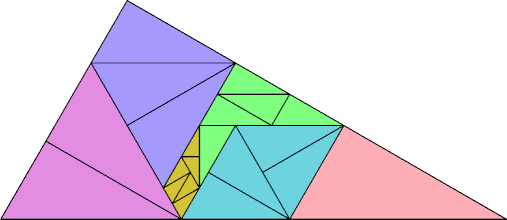
This parallelogrammatic didom and tetradom can be solved with fewer scales than the monomino: