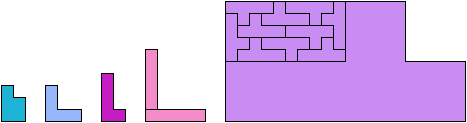
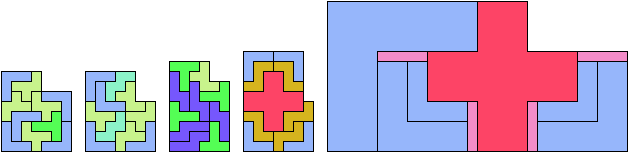
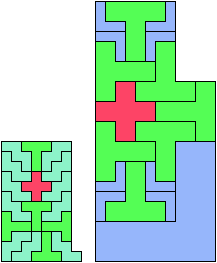
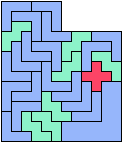
Only five scaled pentominoes can tile L-shaped polyominoes:

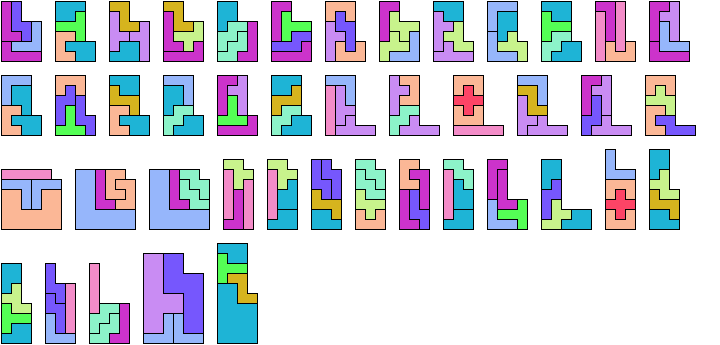
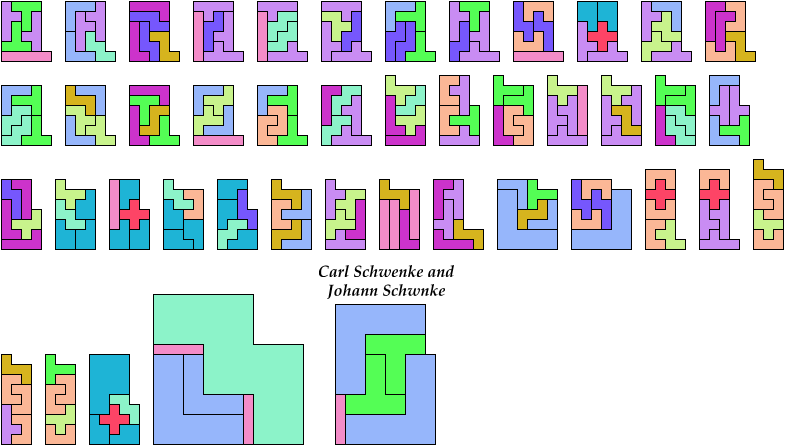
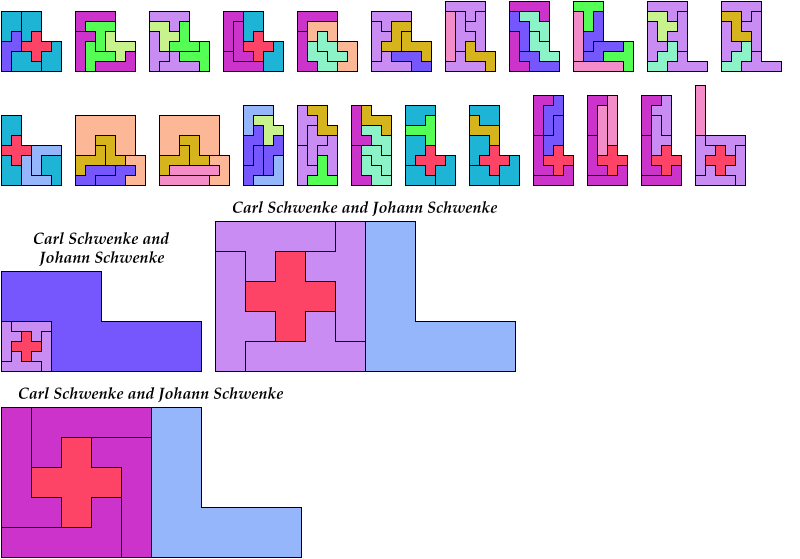
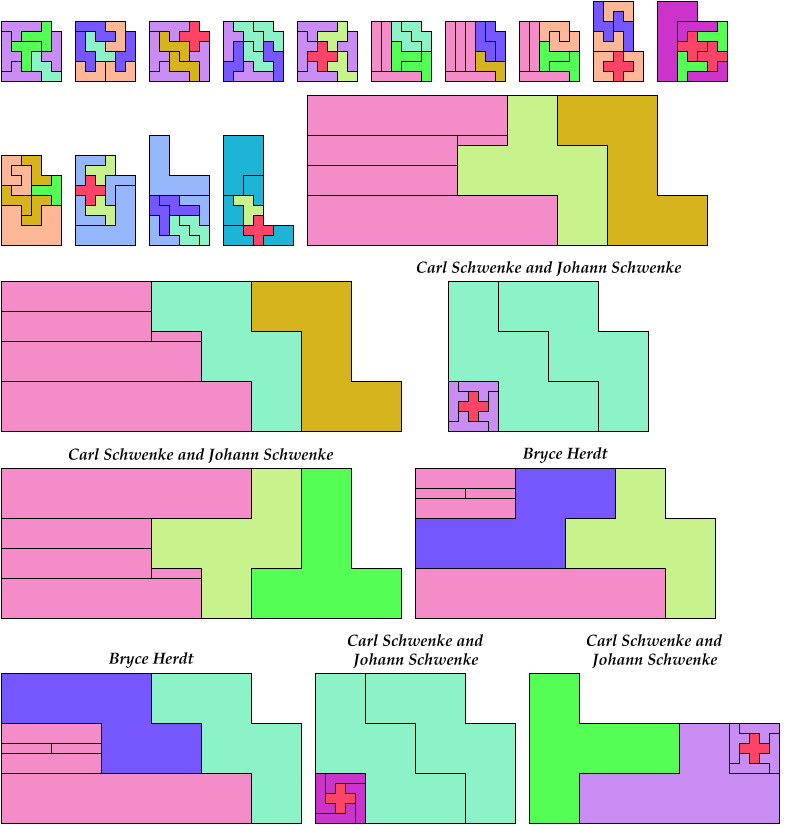
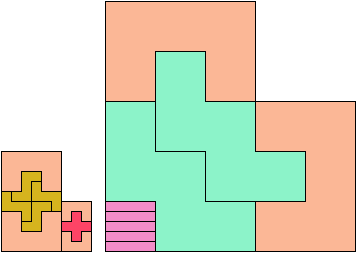
Here I show which sets of three pentominoes can tile an L-shaped polyomino, using the pentominoes at various sizes. If you find a solution with fewer tiles than one of mine, please write!
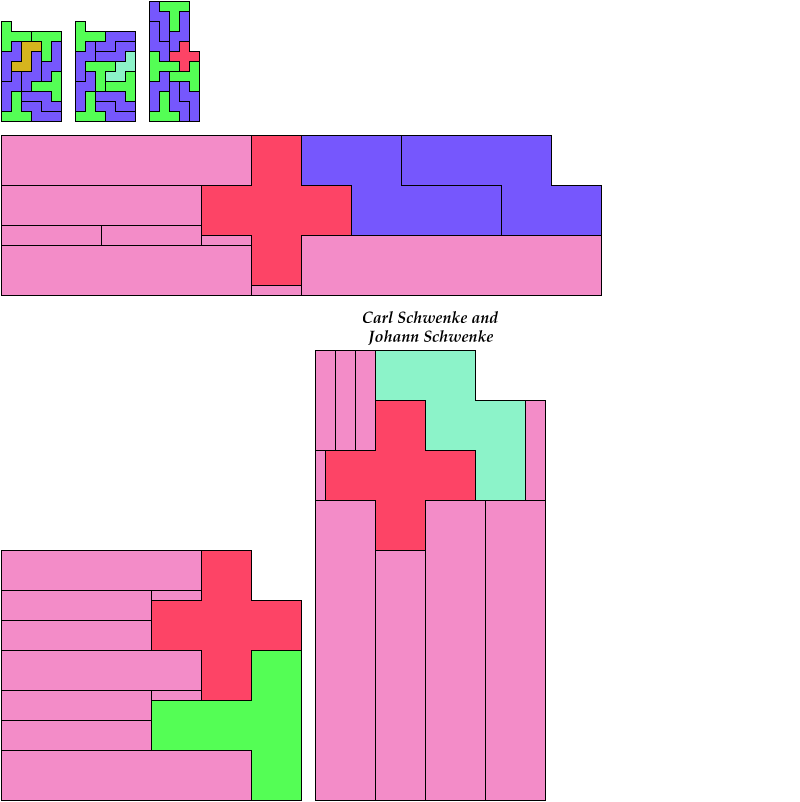
Bryce Herdt contributed improvements. So did Carl Schwenke and Johann Schwenke.
See also L Shapes from Three Pentominoes and Scaled Two-Pentomino L Shapes.

| FIL 4 | FNV 6 | FUZ 5 | INU 5 | IUY 3 | LPV 3 | LWZ 6 | NVW 8 | PVX 6 | TXZ — |
| FIN 7 | FNW — | FVW 10 | INV 4 | IUZ 7 | LPW 4 | LXY 6 | NVX 14 | PVY 3 | TYZ 6 |
| FIP 4 | FNX — | FVX 7 | INW 7 | IVW 5 | LPX 6 | LXZ 8 | NVY 5 | PVZ 3 | UVW 13 |
| FIT 7 | FNY 5 | FVY 5 | INX 11 | IVX 10 | LPY 3 | LYZ 5 | NVZ 3 | PWX 6 | UVX 4 |
| FIU 3 | FNZ — | FVZ 5 | INY 5 | IVY 4 | LPZ 3 | NPT 3 | NWX — | PWY 3 | UVY 3 |
| FIV 5 | FPT 4 | FWX — | INZ 7 | IVZ 3 | LTU 5 | NPU 3 | NWY 7 | PWZ 4 | UVZ 5 |
| FIW 8 | FPU 3 | FWY 6 | IPT 3 | IWX 11 | LTV 4 | NPV 3 | NWZ — | PXY 5 | UWX 14 |
| FIX 12 | FPV 4 | FWZ — | IPU 3 | IWY 5 | LTW 5 | NPW 5 | NXY 6 | PXZ 6 | UWY 4 |
| FIY 5 | FPW 5 | FXY 7 | IPV 3 | IWZ 7 | LTX 8 | NPX 6 | NXZ — | PYZ 4 | UWZ 14 |
| FIZ 7 | FPX 8 | FXZ — | IPW 4 | IXY 6 | LTY 4 | NPY 3 | NYZ 6 | TUV 5 | UXY 5 |
| FLN 5 | FPY 4 | FYZ 5 | IPX 5 | IXZ 12 | LTZ 5 | NPZ 4 | PTU 4 | TUW 15 | UXZ 11 |
| FLP 3 | FPZ 4 | ILN 3 | IPY 3 | IYZ 6 | LUV 5 | NTU 4 | PTV 3 | TUX 12 | UYZ 5 |
| FLT 6 | FTU 5 | ILP 3 | IPZ 3 | LNP 3 | LUW 6 | NTV 5 | PTW 4 | TUY 5 | VWX 27 |
| FLU 3 | FTV 10 | ILT 3 | ITU 7 | LNT 4 | LUX 3 | NTW 11 | PTX 6 | TUZ 7 | VWY 5 |
| FLV 4 | FTW 14 | ILU 4 | ITV 5 | LNU 4 | LUY 3 | NTX 11 | PTY 3 | TVW 5 | VWZ 8 |
| FLW 5 | FTX — | ILV 3 | ITW 7 | LNV 4 | LUZ 5 | NTY 5 | PTZ 5 | TVX 17 | VXY 6 |
| FLX 8 | FTY 6 | ILW 4 | ITX 11 | LNW 6 | LVW 5 | NTZ 11 | PUV 4 | TVY 5 | VXZ 10 |
| FLY 5 | FTZ — | ILX 6 | ITY 5 | LNX 6 | LVX 6 | NUV 6 | PUW 5 | TVZ 6 | VYZ 4 |
| FLZ 4 | FUV 3 | ILY 3 | ITZ 8 | LNY 4 | LVY 4 | NUW 7 | PUX 3 | TWX 17 | WXY 7 |
| FNP 4 | FUW 4 | ILZ 5 | IUV 7 | LNZ 5 | LVZ 3 | NUX 7 | PUY 3 | TWY 7 | WXZ — |
| FNT 10 | FUX 5 | INP 3 | IUW 9 | LPT 3 | LWX 7 | NUY 4 | PUZ 4 | TWZ 14 | WYZ 6 |
| FNU 4 | FUY 3 | INT 6 | IUX 4 | LPU 3 | LWY 5 | NUZ 8 | PVW 4 | TXY 7 | XYZ 7 |
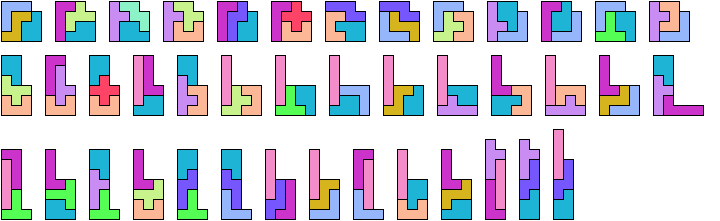


Last revised 2024-03-26.