At his website Atlantis, Dr. Karl Scherer introduced similar or scaled tetrads. These are arrangements of four similar shapes in which each borders the other three. In general, scaled tetrads are easier to find that standard tetrads.
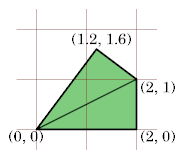
A polydom is a polyform whose cells are 2×1 right triangles. I exclude polydoms that contain a kite didom:

For kiteless polydoms, the orthogonal edges must conform to the square grid.
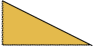
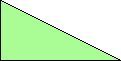
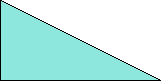
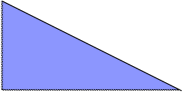
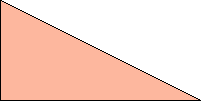
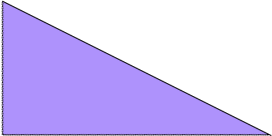
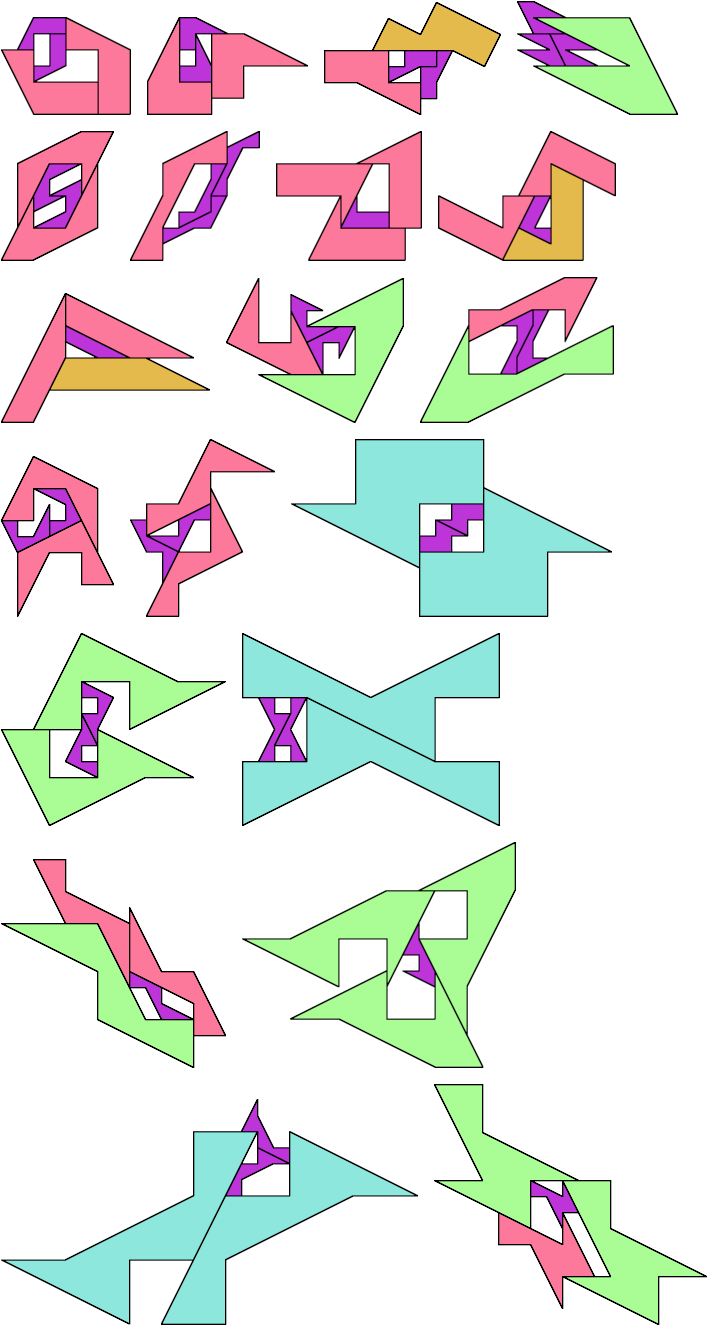
Here I show the smallest known scaled tetrads for polydoms with 2, 3, or 4 cells, keeping to the grid and using scale factors that are integers or integer multiples of √5. If you find a smaller solution or solve an unsolved case, please write.
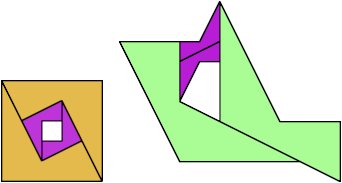
Abaroth found a compact didom tetrad. Bryce Herdt found smaller solutions and solved some unsolved cases.
See also Scaled Polyiamond Tetrads.

| 
| 
| 
| 
| 
| 
|
| 1 | 2 | √5 | 3 | 4 | 2√5 | 5 |

| 
| 
|
| 6 | 3√5 | 7 |

Last revised 2025-11-26.