
The compatibility problem is to find a figure that can be tiled with each of a set of polyforms. Polyomino compatibility has been widely studied since the early 1990s. Polyiamond compatibility was first studied systematically by Margarita Lukjanska and Andris Cibulis, who published a paper about it with Andy Liu in 2004 in the Journal of Recreational Mathematics. While the journal was preparing the paper for print, I corresponded with the authors, supplying the missing hexiamond compatibility and some other solutions. My contributions arrived too late to appear in print, but I was listed as a joint author.
This web page and my other page, Mixed Polyiamond Compatibility, extend and correct the solutions in the JRM article. For sets of three hexiamonds, see Triple Hexiamonds.

| A | E | F | H | I | L | O | P | S | U | V | X | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | * | 3 | 2 | 3 | 2 | 3 | × | 2 | 18 | 3 | 2 | × |
| E | 3 | * | 6 | 2 | 3 | 3 | × | 6 | 4 | 3 | 6 | 3 |
| F | 2 | 6 | * | 2 | 2 | 2 | 6 | 2 | 2 | 2 | 2 | 6 |
| H | 3 | 2 | 2 | * | 3 | 2 | 6 | 2 | 2 | 2 | 3 | 3 |
| I | 2 | 3 | 2 | 3 | * | 3 | × | 2 | 3 | 3 | 2 | × |
| L | 3 | 3 | 2 | 2 | 3 | * | 6 | 2 | 3 | 2 | 3 | 3 |
| O | × | × | 6 | 6 | × | 6 | * | 6 | 3 | 3 | 3 | × |
| P | 2 | 6 | 2 | 2 | 2 | 2 | 6 | * | 2 | 2 | 2 | 2 |
| S | 18 | 4 | 2 | 2 | 3 | 3 | 3 | 2 | * | 2 | 3 | × |
| U | 3 | 3 | 2 | 2 | 3 | 2 | 3 | 2 | 2 | * | 3 | × |
| V | 2 | 6 | 2 | 3 | 2 | 3 | 3 | 2 | 3 | 3 | * | × |
| X | × | 3 | 6 | 3 | × | 3 | × | 2 | × | × | × | * |



| A | E | F | H | I | L | O | P | S | U | V | X | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | * | 3 | × | 3 | 5 | 3 | × | × | 33 | 3 | 5 | × |
| E | 3 | * | × | 3 | 3 | 3 | × | × | 5 | 3 | 15 | 3 |
| F | × | × | * | × | × | × | × | 3 | × | × | × | × |
| H | 3 | 3 | × | * | 3 | 3 | 33 | × | 3 | 5 | 3 | 3 |
| I | 5 | 3 | × | 3 | * | 3 | × | × | 3 | 3 | 9 | × |
| L | 3 | 3 | × | 3 | 3 | * | 15 | × | 3 | 3 | 3 | 3 |
| O | × | × | × | 33 | × | 15 | * | × | 3 | 3 | 3 | × |
| P | × | × | 3 | × | × | × | × | * | × | × | × | × |
| S | 33 | 5 | × | 3 | 3 | 3 | 3 | × | * | 3 | 3 | × |
| U | 3 | 3 | × | 5 | 3 | 3 | 3 | × | 3 | * | 3 | × |
| V | 5 | 15 | × | 3 | 9 | 3 | 3 | × | 3 | 3 | * | × |
| X | × | 3 | × | 3 | × | 3 | × | × | × | × | × | * |

| A | E | F | H | I | L | O | P | S | U | V | X | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | * | × | 2 | 3 | 2 | 4 | × | 2 | ? | 9 | 2 | × |
| E | × | * | 32 | 2 | ? | 6 | × | 6 | 6 | ? | ? | × |
| F | 2 | 32 | * | 2 | 2 | 2 | 42 | 2 | 2 | 2 | 2 | × |
| H | 3 | 2 | 2 | * | 4 | 2 | 12 | 2 | 2 | 2 | 9 | × |
| I | 2 | ? | 2 | 4 | * | 3 | × | 2 | 3 | 4 | 2 | × |
| L | 4 | 6 | 2 | 2 | 3 | * | 10 | 2 | 3 | 2 | 4 | × |
| O | × | × | 42 | 12 | × | 10 | * | 6 | 3 | 3 | 3 | × |
| P | 2 | 6 | 2 | 2 | 2 | 2 | 6 | * | 2 | 2 | 2 | 2 |
| S | ? | 6 | 2 | 2 | 3 | 3 | 3 | 2 | * | 2 | 3 | × |
| U | 9 | ? | 2 | 2 | 4 | 2 | 3 | 2 | 2 | * | 3 | × |
| V | 2 | ? | 2 | 9 | 2 | 4 | 3 | 2 | 3 | 3 | * | × |
| X | × | × | × | × | × | × | × | 2 | × | × | × | * |


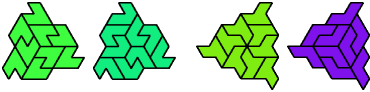
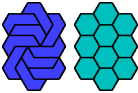
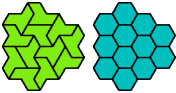

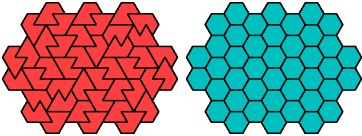

| A | E | F | H | I | L | O | P | S | U | V | X | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | * | ? | 6 | 6 | 6 | 6 | × | 6 | ? | ? | 6 | × |
| E | ? | * | ? | 4 | ? | ? | × | 6 | 6 | ? | ? | × |
| F | 6 | ? | * | 6 | 6 | 6 | 6 | 6 | 30 | 12 | 6 | × |
| H | 6 | 4 | 6 | * | 12 | 6 | 6 | 6 | 12 | 18 | 18 | × |
| I | 6 | ? | 6 | 12 | * | 3 | × | 6 | ? | 3 | 6 | × |
| L | 6 | ? | 6 | 6 | 3 | * | 6 | 6 | 18 | 3 | 6 | × |
| O | × | × | 6 | 6 | × | 6 | * | 6 | 18 | 18 | 18 | × |
| P | 6 | 6 | 6 | 6 | 6 | 6 | 6 | * | 18 | 12 | 6 | 2 |
| S | ? | 6 | 30 | 12 | ? | 18 | 18 | 18 | * | 16 | 18 | × |
| U | ? | ? | 12 | 18 | 3 | 3 | 18 | 12 | 16 | * | 18 | × |
| V | 6 | ? | 6 | 18 | 6 | 6 | 18 | 6 | 18 | 18 | * | × |
| X | × | × | × | × | × | × | × | 2 | × | × | × | * |
| A | E | F | H | I | L | O | P | S | U | V | X | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | * | × | 12 | 6 | 12 | 32 | × | 12 | ? | ? | 12 | × |
| E | × | * | ? | 4 | ? | ? | × | ? | ? | ? | ? | × |
| F | 12 | ? | * | 18 | 12 | 8 | 42 | 12 | 30 | 42 | 12 | × |
| H | 6 | 4 | 18 | * | ? | 18 | 30 | 30 | 24 | 30 | 30 | × |
| I | 12 | ? | 12 | ? | * | 7 | × | 10 | ? | 9 | 10 | × |
| L | 32 | ? | 8 | 18 | 7 | * | 10 | 14 | 24 | 9 | 24 | × |
| O | × | × | 42 | 30 | × | 10 | * | 14 | 24 | 24 | 24 | × |
| P | 12 | ? | 12 | 30 | 10 | 14 | 14 | * | 24 | 24 | 8 | 2 |
| S | ? | ? | 30 | 24 | ? | 24 | 24 | 24 | * | 24 | 24 | × |
| U | ? | ? | 42 | 30 | 9 | 9 | 24 | 24 | 24 | * | 24 | × |
| V | 12 | ? | 12 | 30 | 10 | 24 | 24 | 8 | 24 | 24 | * | × |
| X | × | × | × | × | × | × | × | 2 | × | × | × | * |
Last revised 2023-08-12.