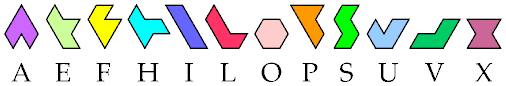
This page shows figures that can be tiled by each of three hexiamonds. It was inspired by Livio Zucca's Triple Pentominoes. For figures that can be tiled by larger groups of hexiamonds, see Multiple Compatibility for Polyiamonds.
Where no closed solution is known, a reëntrant solution is given. If you find a smaller solution, or a closed solution where none is given, please write.
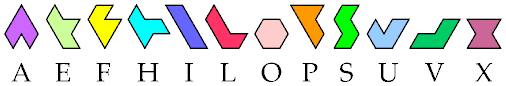
| A-E-F : ∞ | A-E-H : 6 | A-E-I : ∞ | A-E-L : 3 | A-E-O : ∞ |
|---|---|---|---|---|
 |  | 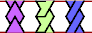 |  | 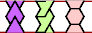
|
| A-E-P : 72 | A-E-S : ∞ | A-E-U : 3 | A-E-V : ∞ | A-E-X : ∞ |
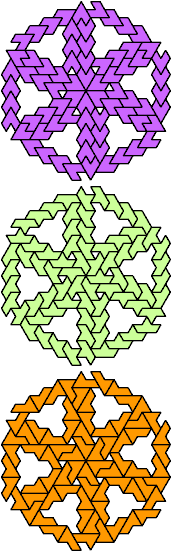 |  |  |  | 
|
| A-F-H : 12 | A-F-I : 2 | A-F-L : 6 | A-F-O : ∞ | A-F-P : 2 |
 |  |  |  | 
|
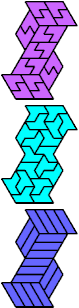
| A-F-S : 54 | A-F-U : 6 | A-F-V : 2 | A-F-X : ∞ | A-H-I : 18 |
 |  |  |  | 
|
| A-H-L : 9 | A-H-O : ∞ | A-H-P : 12 | A-H-S : 54 | A-H-U : 30 |
 |  |  |  | 
|
| A-H-V : 18 | A-H-X : ∞ | A-I-L : 6 | A-I-O : ∞ | A-I-P : 2 |
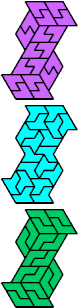 |  |  |  | 
|
| A-I-S : 126 | A-I-U : 18 | A-I-V : 2 | A-I-X : ∞ | A-L-O : ∞ |
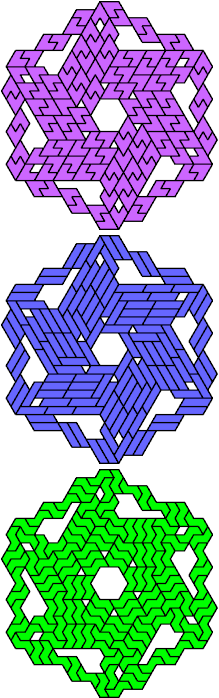 | 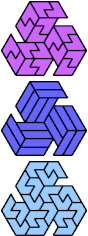 |  |  | 
|
| A-L-P : 6 | A-L-S : 54 | A-L-U : 3 | A-L-V : 6 | A-L-X : ∞ |
 |  | 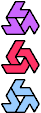 |  | 
|
| A-O-P : ∞ | A-O-S : ∞ | A-O-U : ∞ | A-O-V : ∞ | A-O-X : ∞ |
 | 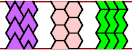 | 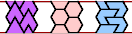 |  | 
|
| A-P-S : ∞ | A-P-U : 18 | A-P-V : 2 | A-P-X : ∞ | A-S-U : ∞ |
 | 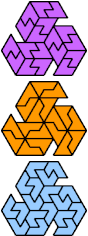 |  |  | 
|
| A-S-V : ∞ | A-S-X : ∞ | A-U-V : 18 | A-U-X : ∞ | A-V-X : ∞ |
 |  |  |  | 
|
| E-F-H : 30 | E-F-I : ∞ | E-F-L : 6 | E-F-O : ∞ | E-F-P : 6 |
 |  |  |  | 
|
| E-F-S : ∞ | E-F-U : 6 | E-F-V : ∞ | E-F-X : ∞ | E-H-I : 3 |
 |  |  |  | 
|
| E-H-L : 3 | E-H-O : ∞ | E-H-P : 6 | E-H-S : 6 | E-H-U : 42 |
 |  |  |  | 
|
| E-H-V : 6 | E-H-X : 3 | E-I-L : 3 | E-I-O : ∞ | E-I-P : 6 |
 |  |  |  | 
|
| E-I-S : ∞ | E-I-U : ∞ | E-I-V : 6 | E-I-X : ∞ | E-L-O : ∞ |
 |  |  |  | 
|
| E-L-P : 6 | E-L-S : 18 | E-L-U : 3 | E-L-V : ∞ | E-L-X : 3 |
 |  | 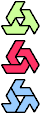 |  | 
|
| E-O-P : ∞ | E-O-S : ∞ | E-O-U : ∞ | E-O-V : ∞ | E-O-X : ∞ |
 | 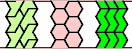 | 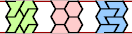 |  | 
|
| E-P-S : 6 | E-P-U : 6 | E-P-V : 6 | E-P-X : 6 | E-S-U : ∞ |
 |  |  |  | 
|
| E-S-V : ∞ | E-S-X : ∞ | E-U-V : ∞ | E-U-X : ∞ | E-V-X : ∞ |
 |  |  |  | 
|
| F-H-I : 6 | F-H-L : 6 | F-H-O : 6 | F-H-P : 2 | F-H-S : 2 |
 |  |  |  | 
|
| F-H-U : 2 | F-H-V : 6 | F-H-X : ∞ | F-I-L : 6 | F-I-O : ∞ |
 |  |  |  | 
|
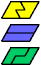
| F-I-P : 2 | F-I-S : 6 | F-I-U : 6 | F-I-V : 2 | F-I-X : ∞ |
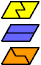 |  | 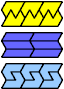 |  | 
|
| F-L-O : 6 | F-L-P : 6 | F-L-S : 6 | F-L-U : 2 | F-L-V : 6 |
 | 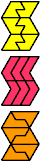 |  | 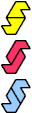 | 
|
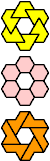
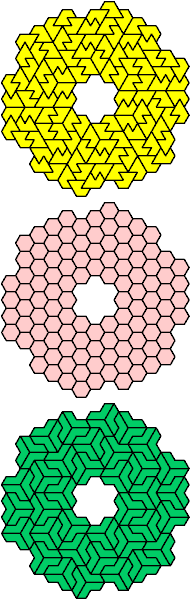
| F-L-X : ∞ | F-O-P : 6 | F-O-S : 108 | F-O-U : 42 | F-O-V : 108 |
 |  | 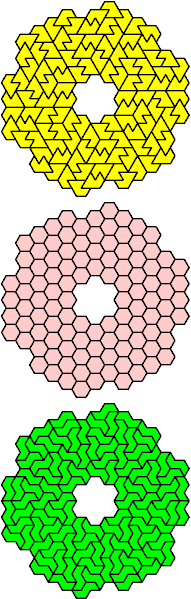 | 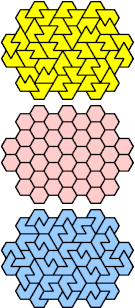 | 
|
| F-O-X : ∞ | F-P-S : 2 | F-P-U : 2 | F-P-V : 2 | F-P-X : 6 |
 |  |  |  | 
|
| F-S-U : 2 | F-S-V : 66 | F-S-X : ∞ | F-U-V : 6 | F-U-X : ∞ |
 |  |  |  | 
|
| F-V-X : ∞ | H-I-L : 3 | H-I-O : ∞ | H-I-P : 6 | H-I-S : 6 |
 |  |  |  | 
|
| H-I-U : 6 | H-I-V : 6 | H-I-X : ∞ | H-L-O : 6 | H-L-P : 2 |
 |  |  |  | 
|
| H-L-S : 6 | H-L-U : 6 | H-L-V : 9 | H-L-X : 3 | H-O-P : 6 |
 |  |  |  | 
|
| H-O-S : 18 | H-O-U : 18 | H-O-V : 18 | H-O-X : ∞ | H-P-S : 2 |
 |  | 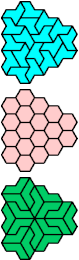 |  | 
|
| H-P-U : 2 | H-P-V : 6 | H-P-X : 6 | H-S-U : 2 | H-S-V : 3 |
 |  |  |  | 
|
| H-S-X : ∞ | H-U-V : 6 | H-U-X : ∞ | H-V-X : ∞ | I-L-O : ∞ |
 |  |  |  | 
|
| I-L-P : 6 | I-L-S : 9 | I-L-U : 3 | I-L-V : 6 | I-L-X : ∞ |
 |  |  |  | 
|
| I-O-P : ∞ | I-O-S : ∞ | I-O-U : ∞ | I-O-V : ∞ | I-O-X : ∞ |
 | 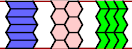 | 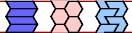 |  | 
|
| I-P-S : 6 | I-P-U : 6 | I-P-V : 2 | I-P-X : ∞ | I-S-U : 6 |
 | 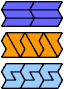 |  |  | 
|
| I-S-V : 27 | I-S-X : ∞ | I-U-V : 18 | I-U-X : ∞ | I-V-X : ∞ |
 |  |  |  | 
|
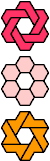
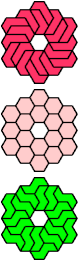
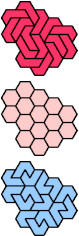
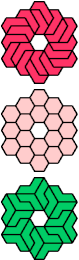
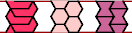
| L-O-P : 6 | L-O-S : 18 | L-O-U : 15 | L-O-V : 18 | L-O-X : ∞ |
 |  |  |  | 
|
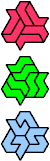
| L-P-S : 6 | L-P-U : 6 | L-P-V : 6 | L-P-X : ∞ | L-S-U : 6 |
 |  |  |  | 
|
| L-S-V : 9 | L-S-X : ∞ | L-U-V : 18 | L-U-X : ∞ | L-V-X : ∞ |
 |  |  |  | 
|
| O-P-S : 6 | O-P-U : 6 | O-P-V : 6 | O-P-X : ∞ | O-S-U : 3 |
 |  |  |  | 
|
| O-S-V : 3 | O-S-X : ∞ | O-U-V : 3 | O-U-X : ∞ | O-V-X : ∞ |
 |  |  |  | 
|
| P-S-U : 2 | P-S-V : 6 | P-S-X : ∞ | P-U-V : 6 | P-U-X : ∞ |
 |  |  |  | 
|
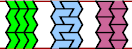
| P-V-X : ∞ | S-U-V : 3 | S-U-X : ∞ | S-V-X : ∞ | U-V-X : ∞ |
 |  |  |  | 
|
Last revised 2014-02-18.