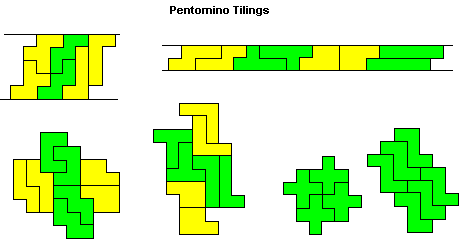
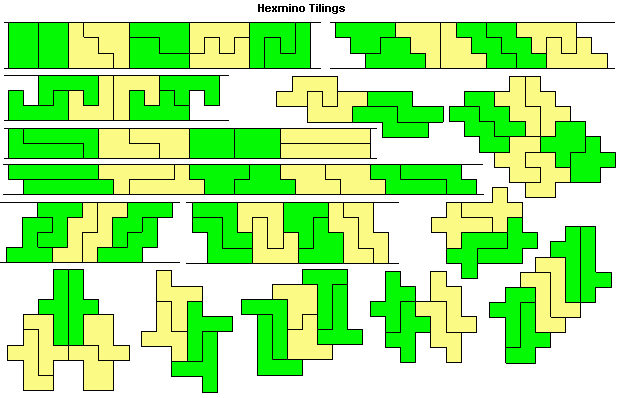
All polyominoes up to the hexominoes will tile the plane (see below for pentominoes and hexominoes).

All but four of the heptominoes tile the plane. The one with the hole obviously will not and the other three can be shown to be non-tilers by simply trying to fill the plane starting from one of the pieces. In the diagram below we start by trying to fill the grey square in A. This leads to situations B and C which in turn lead to D and E (from B) and F and G (from C). We now have grey squares which cannot be filled.

The four heptominoes which do not tile the plane

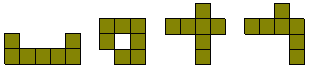
See also Some Polyomino Tilings of the Plane

Some examples of polyiamond tiling are shown below.

For detailed drawings of polyiamond tilings see Michael Dowle's diagrams in Ed Pegg Jr.'s Mathpuzzle.com

All polyhexes up to the pentahexes will tile the plane (see diagrams below).

All polycubes up to and including the hexacubes will tile space. The monocube, dicube and tricubes all tile simply and as for the tetracubes the ones which are solid tetrominoes tile as their tetromino counterparts do. The remaining three all form 2x2x2 cubes with themselves.

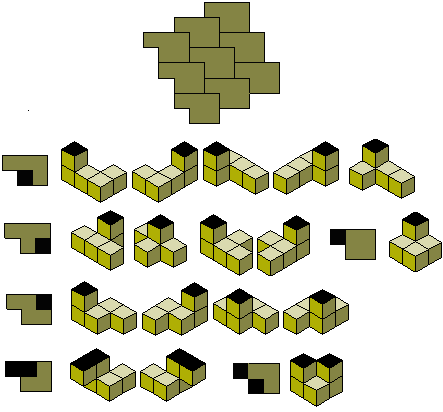
For the pentacubes we firstly note that the solid pentominoes tile space by means of single layers in the same way the pentominoes tile the plane. For the remainder we look at the diagram below. At the top is a tiling of the plane with pentominoes such that they are all in the same orientation. If from this we remove one cube and place it above (or below) the remainder of the pentomino then we have a tiling of one layer with symmetrically placed holes and another layer above (or below) with single cubes in the same pattern as the hole. A second layer can be placed above (or below) filling the original layer completely. This can be continued indefinitely to tile space. The rest of the diagram below shows how the various pentacubes can tile using this pattern. There are three pentacubes that cannot be tiled this way but if we remove two cubes from each layer and do the same as the above we again tile the plane (see bottom row of the diagram).

All hexacubes tile space. The 35 solid hexominioes tile and all but six of the others tile space from one or more of the hexomino tilings in a manner similar to the pentacubes.

The remaining six hexacubes can be tiled as shown below. The diagram on the right is for the hexacube at the top left of the group of four and the other three tile with simple variations of this pattern. In each case a construction is formed which continues indefinitely and then can be joined with other such constructions to tile space.

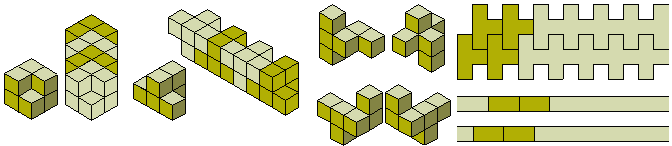
Of the four heptominoes which do not tile the plane there is one for which the corresponding heptacube will tile space. In fact ten of them will form a 2x5x7 box (see below).

The diagram show (i) a single copy of the heptacube; (ii) three pieces joined; (iii) a second set of three pieces filling the 'gap' in the first three and (iv) the box completed with four more copies of the heptacube.