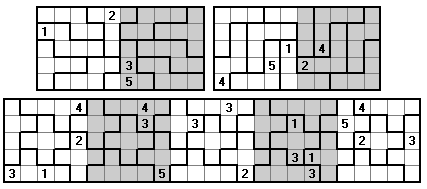
The pentominoes cannot form Sudiku type problems for either a 5x5 or 5x10 rectangle and so these problems use some different variations of the Sudoku theme. These are base on the various rectangles which can be made with the full set as detailed below.
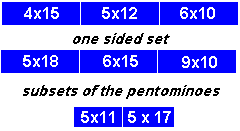
The following problems are based on a 5x12 rectangle made from the 12 pentominoes. Since these do not make a number of 5x5 panels the figures are divided up as shown below with some special conditions.
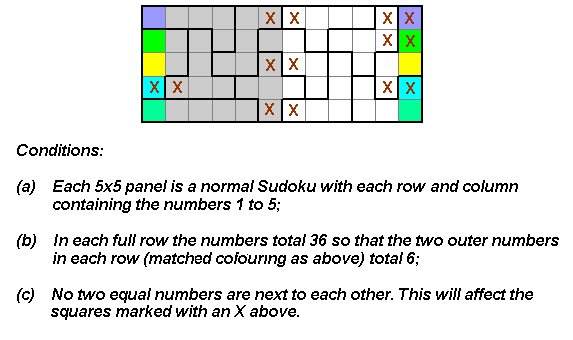
These examples have only five clues given.
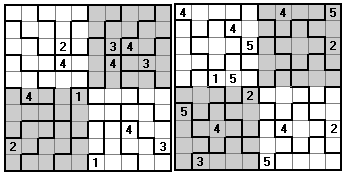
Here, instead of a full set , we look at a 5x12 rectangle made with copies of two pentominoes.
This final example has only three clues. While the solution is unique it is all but impossible to do by hand.
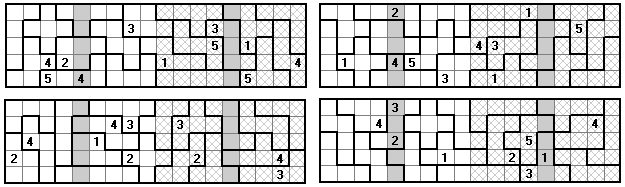
If we change the conditions so that the 1st and 6th, and 7th and 12th, columns are identical and remove the condition that no equal numbers adjoin while still keeping rows sums at 36 we get a two clue solution which can be done by hand quite easily.
(a) the top and bottom rows are identical and (b) no two equal numbers are next to each other.
The next few problems use a 4x15 rectangle with the following conditions -
| (a) in each panel the rows contain 1 to 5; |
| (b) in each panel one number is omitted from each column. The number omitted is different in each column but the pattern of numbers omitted is the same for each panel. Thus if the numbers omitted in the first panel are, in order, 12345 then the numbers omitted in the other two panels are likewise 12345 in that order; |
| (c) no two equal numbers are next to each other |
These are examples of Missing Number Sudoku and other examples are here.
Here we use a 5x18 rectangle made from the 18 one-sided pieces. Each half (5x9) is made up of two overlapping 5x5 Sudoku panels with the added condition that no equal numbers adjoin.
Here, as with the 6x10 above, we have the bottom row the same as the top row with no equal numbers adjoining.
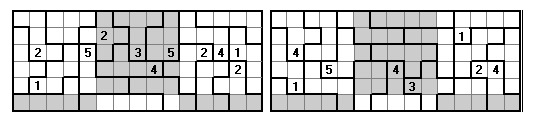
Here, as with the 5x18 above, we have two 5x9 rectangles made up of two overlapping 5x5 panels.

If we omit the 5x1 rectangle from the set we can form 5x11 rectangles. The conditions here are
| (a) in each panel (white) the rows and columns contain 1 to 5; |
| (b) the entries in columns 1, 6 and 11 (the two outer and the central columns) are identical. |
If we omit the 5x1 rectangle from the one-sided set we can form 5x17 rectangles. Here we have three 5x5 panels and two single colums with the condition that no two adjacent numbers be equal.
The following problems have the same setup with the added condition that in each row the numbers add to 51
Other Pentomino Based Problems
If we look for problems with full sets of panels then we cannot use the full set of pentominoes. In these problems we have just the normal conditions. These first examples use just a single piece.
Using pairs of pieces we can get a number of other problems. In the first examples we have the extra condition that no adjoining numbers are equal.