The term rectifiable is probably not the best one to use for polyiamonds since they will not, of course, form rectangles. What they can form is triangles, trapezia, parallelograms and hexagons. Obviously a polyiamond which can form a triangle can also form a trapezium or hexagon and one which will form a trapezium will also form a parallelogram.

Mike Reid has supplied a great many suggestions as to directions of research for this page especially into the possible polyiamond pairings.

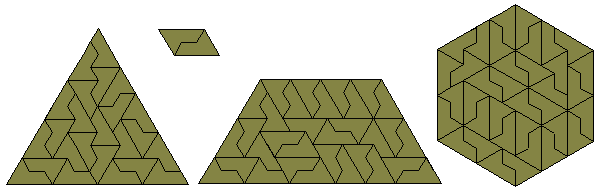
The diagram below shows an hexiamond filling a triangle, a trapezium, a parallelogram and a hexagon..

The triangle, parallelogram, and hexagon formed are the smallest possible with this polyiamond. Any polyiamond which forms a parallelogram can also form a hexagon. An example of this is shown below where 6 copies the hexiamond parallelogram above are joined to make a rhombus and then the three rhombi are joined to make a hexagon of side 6 (this is a simpler version of the one in the diagram above).

Notice also that two copies of the trapezium above can be joined to give a hexagon of side 8. This trapezium is not the smallest possible as shown in the diagram above sent to me by Mike Reid. The diagram at the centre (also due to Mike Reid) shows a simpler version of the triangle where 8 hexiamonds form one third of the full triangle.

The figure on the left of the diagram below shows an octiamond which forms a hexagon but no triangle, parallelogram or trapezium can be formed. The figure at the right shows a hexiamond which forms a parallelogram but cannot form a triangle or trapezium It can, of course, form a hexagon of side 8.

The above statements about the hexiamond are easy to prove. If we consider an edge of a trapezium (or triangle) of side n then the diagram below shows that in order to fill such an edge we must also be able to fill a smaller edge which would eventually lead to an impossible situation.

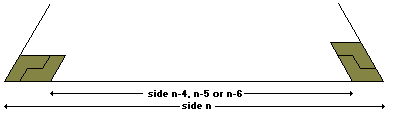
'Rectifiable' polyiamonds are much rarer that rectifiable polyominoes. For example, even the simple looking pentiamond cannot form a parallelogram, trapezium or triangle. We can see this by considering the following. First if we look at a straight edge which needs to be filled with polyiamonds we see that each polyiamond can contribute one of three type sections to the edge (see A, P and B below).

Now if we try to use the pentiamond to fill a triangle we see we shall need to fill a B type space at some point and since the pentiamond has only P and A type edges this is not possible. Next if we consider the parallelogram and trapezium we see we must fill a 120 degree corner and this can be done in one of four ways.

Cases 2, 3 and 4 are eliminated immediately as they require B type edges on both sides and all we are left with is the situation in 1 and this could only provide a solution to the trapezium and then only if the top edge were the shorter of the parallel sides. However if this were the case then the same configuration would occur at the right hand side of the top edge producing a B type gap which could not be filled. Notice, however, that this pentiamond can form a hexagon (see below).

In the above figure the hexagon is divided into six congruent regions one of which if filled with the pentiamond. Unlike rectangles, triangles, parallelograms and rhombi, a number of hexagons cannot combine to make a larger one and so the concept of 'prime' hexagon has no meaning. Thus in order to investigate all possible hexagons we need to find a diagram such the one below. In this the central hexagonal area is filled as above and then pentiamonds are used to create rings around it to make hexagons of side 10, 15, 20 etc.

This polyiamond also illustrates another interesting difference between polyiamonds and rectifiable polyominoes. For the polyominoes there is no known example of one which can tile a half strip and yet not tile a rectangle. This pentiamond can, however, tile a half 'strip' as shown below.

Since the polyiamonds, unlike the polyominoes, form a number of regular shapes it is probably best to define three 'orders' -

T-order : the smallest number of a polyiamond which forms a triangle

P-order : the smallest number of a polyiamond which forms a parallelogram

H-order : the smallest number of a polyiamond which forms a hexagon

 

In the following we shall, in general, ignore those polyiamonds such as the hexagon hexiamond which produce one of these figures trivially.

Pentiamonds

Of the four pentiamonds (above) 1 is itself a trapezium and can form parallelograms and hexagons; 2 we have shown above forms hexagons only (of any side 5n); 3 cannot form any regular shape and 4 can form a hexagon of side 5 but can form neither a parallelogram nor a triangle as shown below.

The diagram at the left shows how a 60º corner could be filled by the pentiamond. If we now try to fill the yellow shaded triangle we get one of the figures at the right which produce situations in which the green triangle cannot be filled thus showing that the 60º angle cannot be formed. This proves that no parallelogram or triangle can be formed with pentiamond 4.

The hexagon formed with pentiamond 4 is shown below.

If we look at pairs of pentiamonds then we find that a number of pairs do form triangles.

The above shows triangle made with 3 and 4; 1 and 4; 1 and 3; 1 and 2; and 2 and 4. Pieces 2 and 3 definitely do not form a triangle. Mike Reid conjectures that the 15 edge triangle with 1 and 3 is the smallest possible. The figure below shows a trapezium made up of these pieces which would provide another solution to the triangle but also can be used to extend the triangle to form any triangle of side 15n+5.

Hexiamonds

Of the twelve hexiamonds only the sphinx can form a triangle or trapezium (see above) and four (excluding the trivial case of the rhomboid) can form a parallelogram.

The triangle formed by the sphinx is the smallest possible as can be seen from the following argument.

Firstly, since the number of unit triangles in a triangle of side n is n any triangle formed with an hexiamond must have a side which is a multiple of 6. If we consider the smallest such triangle (side 6) shown below we see that with the colouring shown there is an excess of 6 yellow triangles.

Each sphinx has an excess of 2 and since there must be 6 pieces in any solution the excess must be a multiple of 4 which shows that the construction is impossible. This argument applies equally to any triangle of side 12k+6 and so only triangle of side 12k are possible. These can, of course, be made from the side 12 triangle shown above.

All of the pieces forming parallelograms above can, of course, also form hexagons but in addition both the shoe and the club can form hexagons. In the case of the club four pieces make a hexagon of side 2 and for the shoe 9 are required to hexagon of side 3 thus making the shoe have an odd H-order.

In fact the club can form any hexagon of side n for all n except n = 4. This is shown in the diagram below (from data by Mike Reid) where the club forms hexagons of side 3 and 7. The figure at the right shows how any hexagon can be extended by 3 thus proving the assertion.

There are some pairs of hexiamonds which form a triangle as shown below. In looking for these pairs we do not use the sphinx which itself can form a triangle.

The above triangles are probably the smallest possible for each of the pairings shown.

The 12-12 trapezium above can be extended by the construction at the right to form any (12+2n)-12 trapezium. This will allow the Yacht-Crown 18 sided triangle to be extended to form any triangle of side (18+12n). Also the Yacht-Crown 24 sided triangle can similarly be used to form a triangle of side (24+12n). This shows that any triangle of side 6n can be formed for all n>2.

Notice that the yacht occurs in all the above. In fact it must occur in all possible pairings as shown below.

One of the pieces must have a B type edge i.e. we must have the yacht or the butterfly. Now suppose we have the butterfly but not the yacht. We must also have an hexiamond which will form a corner. The corner forming hexiamonds are Lobster, Rhomboid, Bat, Yacht and Sphinx. We are now looking for Lobster-Butterfly or Rhomboid-Butterfly pairings and it is easy to show that these cannot form a triangle.

The above are, in fact, the only possible pairings as can be seen by trying to form a B type edge with the yacht and any of the other hexiamonds.

Heptiamonds

None of the heptiamonds form any regular shape in a simple way and it may be that none of them do in any way. Some pairs do form figures, however, as shown below.

Triangles

Parallelograms

Trapezia

Hexagons

Octiamonds

Only one octiamond is known to form a triangle as inthe triangle of side 32 below. This was constructed by Karl Scherer and appears in his book "A Puzzling Journey to the Reptiles And Related Animals". Notice how most of the construction consists of parallelograms formed by pairs of the octiamond with only 20 of the 128 pieces outside of a parallelogram.

The next construction shows how the above can be extended to form a triangle of side 48. Similar constructions can form triangle of side (32 + 16k).

Mike Reid has also constructed a 13x24 parallelogram.

It is probable that none of the other octiamonds will form triangles but some form other figures as shown below.

Many pairs form triangles and other figures as shown by the samples below.

The diagram at the bottom right above is one third of a triangle of side 24.

 

Enneiamonds

It seems unlikely that any of the enneiamonds will form a triangle but a number form parallelograms and hexagons.

There are many pairings of pieces which form triangles. The diagrams below show some, but certainly not all, possibilities.

The above triangles are just some of the possibilities and no full analysis has been done. The diagram below shows a pairing which forms triangles of side 9, 12 and 15. The triangle of side 9 can be extended with the construction at the left to form any n-9 trapezium and this in turn can be used to extend any triangle of side n to side (n+9). This shows that triangles of side 3n are possible for all n>2. Triangles of side 3 and 6 are impossible.

Another two of the pairings above can also form triangles of side 3n for n>2 as shown by the diagram below.

Another way in which multiple triangles may be formed is shown below where we see triangles of sides 9, 12 and 15 and another pattern (a triangle of side 21) where the centre of the figure is made up of trihexes which in turn are produced by pairs of an enneiamond. This type of construction can almost certainly be expanded to form any triangle of side 3n where n>2. Another method of forming these larger triangles is shown at the bottom right where borders are formed around existing triangles to form larger ones (these constructions are by Mike Reid).

Higher Order Polyiamonds

The two octiamonds in the hexagon of side 4 are simple examples of general polyiamonds which form hexagons. The diagrams above can be simplified as below.

These can be generalised to give a family of 2n-iamonds which fill an n-sided hexagon using 3n copies.

This result is summarised below -