

An n-omino is a shape made up of n squares joined by complete edges. It could also be thought of as a set of squares cut from a square grid. In the diagram below the three figures on the left are polyominoes but the two on the right are not
For a list of numbers of polyominoes up to order 28 see Tomás Oliveira e Silva's polyomino enumeration, Kevin L. Gong's The Mathematics of Polyominoes , Klarner's Lattice Animal Constant or Sloane's On-Line Encyclopedia of Integer Sequences (this also has links to symmetric polyomino numbers). For diagrams of polyominoes up to size 12 see Ambros Marzetta's List of polyominoes of order 4..12.
There is also some information in Polyominoes, etc. by Beeler, M., Gosper, R.W., and Schroeppel, R, Slavik Jablan's Polyominoes, Enumeration of Remarkable Families of Polyominoes by Dominique Gouyou-Beauchamps, Lawrence Detlor's Polypleura and Description des polyominos (in French).
To experiment with drawing some polyominoes try Phil's Polyomino Maker
For more technical information on the counting problem see A Procedure for Improving the Upper Bound for the Number of n-ominoes and A Finite Basis Theorem Revisited.
![]()
There are five tetrominoes (see above). Unfortunately, although they cover a total area of 20 squares they cannot be joined together to form a rectangle. This can be seen by considering the colouring of the pieces shown above. The first four pieces cover two white and two black squares but the last must cover three of one colour and one of the other. Since any rectangle with area 20 would have 10 black and 10 white squares under such a colouring no such rectangle can be made. The tetrominoes can be joined to form some interesting shapes however and the diagram below shows how they can fit into a 3x7 rectangle with one square omitted. Notice that of these patterns were coloured black and white they would have 11 squares of one colour and 9 of the other.

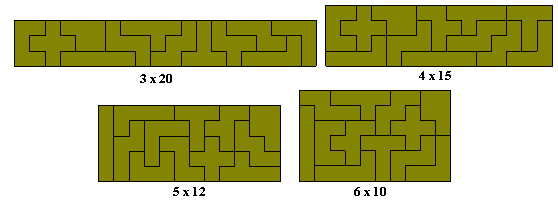
There are twelve pentominoes covering an area of 60 squares. This area can be made up with rectangles 2x30, 3x20 (2 solutions), 4x15 (368 solutions), 5x12 (1010 solutions) and 6x10 (2339 solutions). Since at least one of the pentominoes is of length 3 in two directions the 2x30 is not possible but all the others are (see below). The links above will show images of all solutions (some browsers may not be able to display the 2339 solutions of the 6x10).
The 5x12 and 6x10 rectangles can be made up of two 5x6 rectangles. There are eight solutions shown here.
Patrick Hamlyn has analysed the solutions of the various rectangles to determine which can be coloured with only three colours. He has found the following information on numbers of rectangles which can be three coloured. Strict colouring demands that no two identically coloured pieces touch even at a corner whereas non-strict colouring allows corner touching. No solution can be two coloured.
Three of the rectangles above can be coloured with three colours two with strict colouring - click here to see the image. As you can see from the numbers three coloured solutions can be quite rare with only 4% of the 6x10 rectangles having a strict three colouring. None of the rectangles will allow a two coloured solution. For the 4x15 rectangle there are just five essentially different ways to make a 4x5 and a 4x10 rectangle with the set. All these solutions can be three coloured.
To see a lists of solutions with diagrams go to Adrian Smith's Pentomino Relationships, Pentominos by Lars Kindermann, Eric Wassenaar's Introduction to Polyominoes or All Pentomino Solutions.
For just the 6x10 rectangle see also Wilfred J. Hansen's Equivalence Classes Among Pentomino Tilings of the 6x10 Rectangle
For an animation of the construction of a 3x20 rectangle see Michelle Raymond's Homepage or for animated solutions of all rectangles see Lars Kindermann's Pentominoes.
To try filling a 6 x 10 rectangle go to Robert's Neat Math Page - Pentominoes
Puzzlecraft sells a CD with a large number of pentomino problems.
Other sites with pentomino content are
Also Rudolfo Kurchan's Puzzle Fun has regular pentomino competitions.
There are 35 hexominoes. Unfortunately, as with the tetrominoes, an odd number of these have a 4-2 chessboard colouring and so no rectangle can be filled with all 35. The 11 hexominoes with a 4-2 colouring are shown in the right hand part of the figure below where the remaining 24 pieces form two 8x9 rectangles.



It is also possible to make three 6x12 rectangles or four 6x9 rectangles.

The one-sided trominoes, tetrominoes, pentominoes and hexominoes cover a total area equal to that of a side 22 square. Patrick Hamlyn has proposed the problem of fitting the pieces into this square with as many internal squares formed as possible. Five examples of this are shown here with up to 14 squares.
There are 108 heptominoes one of which has a 'hole' and so again no rectangle is possible with the full set.
You can see an octomino construction at Kadon Enterprises which sells sets of pieces.
David Bird has also made some constructions with octominoes and at least one with enneominoes. (These drawings have been supplied by Mike Reid)
Patrick Hamlyn has produced (by computer) a set of nine 7x47 rectangles each with a central hole with the octominoes.
Until 2005 only one enneomino pattern was known until Peter Esser produced five copies of the 17 x 137 rectangle below.
Peter Esser has noted that there are 1248 enneominoes if we omit the ones with holes and has produced a set of sixteen rectangles with the set.
Patrick Hamlyn has gone one stage better and produced 48 rectangles and believes that 96 might also be possible.
Peter has also produced this dekomino pattern.
| Hello Polyomino (this has a good list of other links) |
| Pentominoes at Multimania (in English and French) |
| Alberto Del Lungo's Medians
of polyominoes: a property for the reconstruction |
| Aad van de Wetering Polyominoes (in Dutch) |
| Pentomino Fuzion Puzzles |
| David Eppstein's Geometry Junkyard |
| Michael Keller's World Game Review has some information on polyominoes |
| The Combinatorial Object Server has information and links |
| Miroslav Vicher's Puzzles Pages |
| Pentomino hungarIQa has an interesting variation on pentominoes - this appears to be a rediscovery of Kate Jones' Rhombiominoes |
| Ali Muniz has a page of polyomino covering problems |
| Martin Watson's Puzzles |
| Edo Timmermans has an article on Polyominoes inside minimal circles |
| Kevin Gong's Welcome to Polyominoes |
| Students of T.I.D. RONSE school in Belgium have a project on pentominoes |