![]()
An n-iamond is a shape made up of n equilateral triangles joined by complete edges. It could also be thought of as a set of triangles cut from an isometric grid. In the diagram below the three figures on the left are polyiamonds but the two on the right are not

A list of the numbers of polyiamonds for a given value of n is available at Sloane's On-Line Encyclopedia of Integer Sequences which also has the numbers of one-sided polyiamonds.
There are 12 hexiamonds which cover an area of 72 triangles. These are shown below with the names by which which they are usually known.
With this area they could fill 3x12, 4x9 or 6x6 parallelograms. The 4x9 and 6x6 are possible but the 3x12 is not and there are just 48 solutions for the 3x11 all of which omit the bat.. The only other 'regular' shape which could be formed is a trapezium. And one can, in fact, be formed. This is shown below with two other symmetric patterns formed with the full set.
The 72 triangles are just sufficient to form a triplication of an octiamond. For various reasons only 24 of the octiamonds can be triplicated. These are shown below (solutions by Pieter. Torbijn).
Similar hole constructions are also possible.
One sided hexiamonds
If we consider mirror image pairs as distinct then there are 19 hexiamonds. The full set cannot form any trapezium or parallelogram although 18 of the pieces can form a 3x18 parallelogram in 1440 ways. The solution below is in the form of two 3x9 parallelograms and all solutions decompose into two parallelograms. The number of solutions for the various decompositions is 4-14 (16); 5-13 (212); 6-12 (332); 7-11 (356); 8-10 (324) and 9-9 (200). Notice that one of the two snakes is absent from the solution below - this piece is absent from all 1440 solutions.
The set can, however, form simultaneous pairs of triplications with the piece triplicated omitted. The first four solutions here are by Pieter Torbijn who also claimed that these were the only solutions. However, Mike Reid recently found a solution for another one (see bottom right).
Mike Reid has also found a solution to the similar hole problem for this set.
If we allow no rotation of pieces then there are 49 hexiamonds. This solution was found using Peter Esser's trisolve program.
Note: In the remainder of this page reference will be made to various trapezia to made with polyiamonds. We shall use the term a-b trapezium to denote the figure shown below. Thus the trapezium above will be referred to as 7-4 trapezium.
There are 24 heptiamonds and they can form a number of parallelograms - 7x12, 6x14, 4x21 and 3x28. These are shown here by way of two 3x14, three 4x7 and two 6x7 parallelograms. Also 1-12, 11-6 and 19-4 trapezia are possible with the last one divided into three 5-4 trapezia.
There are 66 octiamonds which can form 4x66, 6x44, 8x33, 11x24, 12x22 parallelograms as well as 64-4, 29-8 and 16-12 trapezia. The diagram below shows the simultaneous construction of two 4x22 and two 4x11 parallelograms; three 8x11 parallelograms and a 6x44 parallelogram.
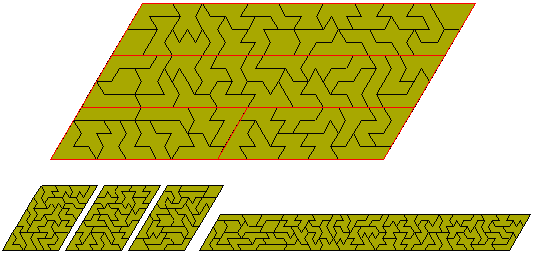
The pattern below provides a solution to the 29-8 trapezium and, by rearrangement (with reflection of the area to the left of the red line) a solution to the 64-4 trapezium. The two trapezia can also be joined to give a 4x44 parallelogram. The other trapezium is the 16-12.


One problem which has been considered with the octiamonds is the simultaneous quadruplication and septuplication of an octiamond. A solution to five of the 66 problems thus posed is shown below. Note that the octiamond to be enlarged is omitted.
Another figure made with the octiamonds is the hexagon below.
Higher Order Polyiamonds
Ed Pegg is producing sets of the 448 dekiamonds for sale. He also has pictures of them on his site as well as pictures of the hendekiamonds and the dodekiamonds.
Patrick Hamlyn has produced these dekiamond constructions (click on the first image to see a larger version).
Patrick Hamlyn has also made another version of the strip above in which the pieces can be coloured with three colours only. This too 27.5 hours of computer time to produce.
One construction which should be possible for the dekiamonds is to make four copies of the trapezium shown below. Unfortunately the dekiamonds are unbalanced in triangle colouring and so one of the trapezia would need the hole in a different position.
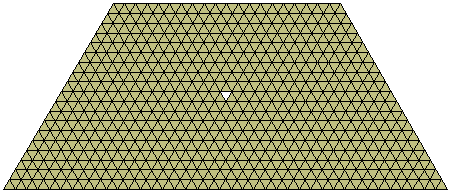
Patrick has also produced the following 43 congruent piece construction using the 1161 hendekiamonds without holes.

Links
| Polyiamonds |
| Les pentamants (in French) |
| Miroslav Vicher's Puzzles Pages |