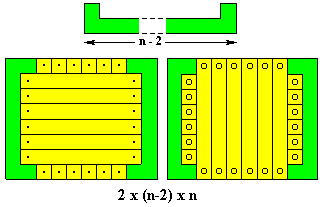
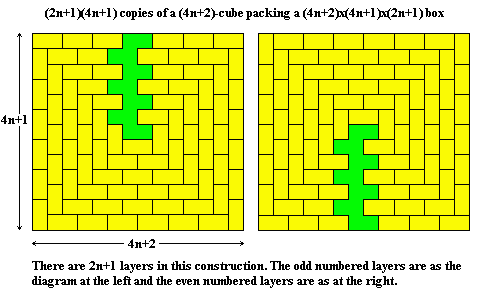
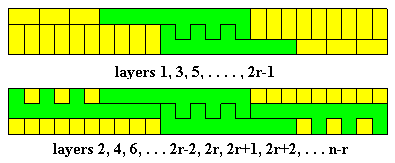
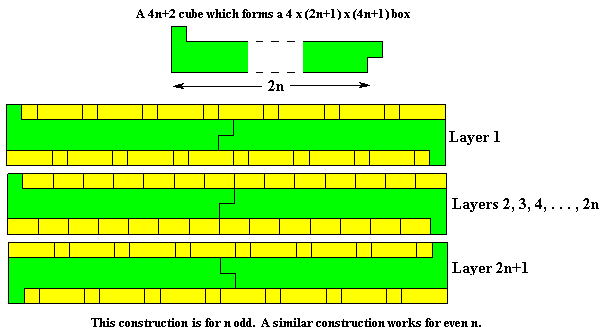
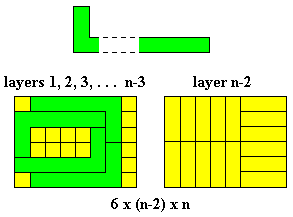
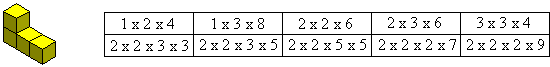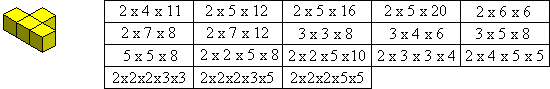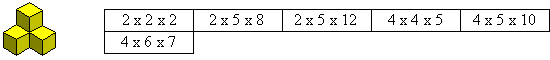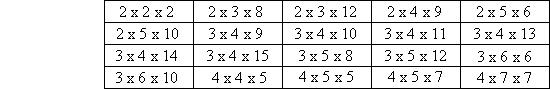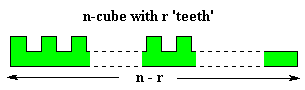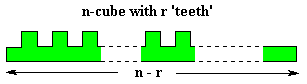As with polyominoes in rectangles we can sometimes pack sets of congruent polycubes into 'boxes'. A lot of information on this is given in Tiling and Packing results of Torsten Sillke - Packing Polycubes and this page will provide a sample of the data available and include some results not found elsewhere on the Internet.

The diagrams on this page use the convention that a dot represents a continuation upwards, a circle downwards and a dot in a circle shows continuation up and down.

Tetracubes

With one notable exception all prime boxes for the tetracubes are known for all dimensions. The list of prime boxes are given below. The left hand column gives the three dimensional boxes and four and five dimensional primes are listed in the right hand column. Diagrams are also available for all these boxes.

This is the only tetracube for which the full set of primes is in doubt. It is possible that a prime of the form 3 x m x n could exist.

This is the only tetracube where we must consider mirror images. This leads to two sets of prime boxes - with and without using both pieces.

If the mirror pairs are considered the same then there are 5 prime boxes.

If, however, we consider mirror pairs as distinct then there are 20 prime boxes.

Pentacubes

Below is a construction using eight Y-pentacubes to form a solid which is half of a 4 x 4 x 5 box.

A lot more information is avaliable on pentacube packing in Torsten Sillke's site. In particular he has a Y-pentacube page.

Of the 12 solid pentominoes, all but the X can form boxes. Many of the constructions are made from 'modules' of groups of pieces which are then combined to form the box. Samples of the possible boxes can be seen here.

Of the remaining 17 three dimensional pentacubes all but two (a mirror pair) can form a box. Sample diagrams can been seen here.

Hexacubes

These are detailed on a separate page.

Not much work has been done with the higher polycubes in boxes although Mike Reid has probably the greatest amount of information much of it. This is now available on his site.

There is one octacube of particular interest which forms a box with only three copies. This does, however, require that both of a mirror pair be used.

Generalisations

There are several classes of polycube which can form boxes and some examples are shown below.

The generalised U n-cube above forms a 2 x (n-2) x n box as shown. In this, and all other examples, the diagram of the construction is for a particular example (here n = 10). In subsequent diagrams in this section the dots and circles will be omitted but the constructions are simple enough to follow. Also in these diagrams, as above, the full shape (when in a layer) will be coloured green and the parts of a shape in different layers will be yellow.

The hexacube above which forms a box with 15 copies is the smallest example of a general odd polycube of size 4n+2 which forms a box with an odd number of pieces.

Mike Reid has produced a similar construction to the above for the 4n-cube

to make a 2n x (4n-1) x 4n box. Another generalisation of his is shown below.

This n-cube forms a 3 x (n-r) x 2n box as shown below where n = 13 and r = 3.

A similar construction also makes a 3 x (n-r) x 2n for the n-cube below.

Mike has also produced a number of other generalisations some of which are shown below.

 

If the above n-cube is given depth 2 to make it a 2n-cube then the above can be simply modified to give a 6 x (2n-4) x 2n box.