Livio Zucca has introduced a new set of polyforms he call sexominoes. He defines them as squares with three different types of edge - male, female and neuter. These are treated as one-sided as can form the rectangle shown below.

Livio Zucca has introduced a new set of polyforms he call sexominoes. He defines them as squares with three different types of edge - male, female and neuter. These are treated as one-sided as can form the rectangle shown below.

Pierpaolo Bernardi did an exhaustive search and found 147 928 solutions to the above in July 2001.
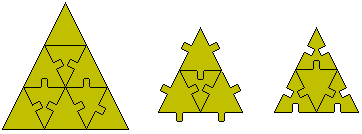
Similarly we have forms based on an equilateral triangle.
Using the same methods with hexagons we get 92 pieces. This solution is by Miroslav Vicher (May 2000)r.
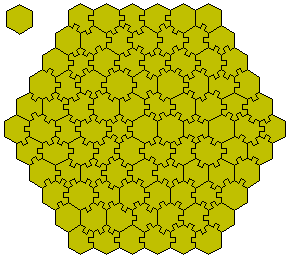
If we count reflections as distinct we get 130 one sided pieces. This solution is again by Miroslav Vicher.
Generalisation
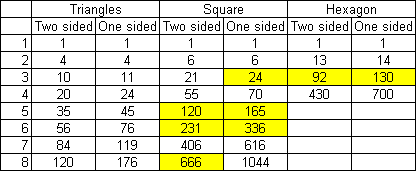
If we use squares and add a fourth edging type - hermaphroditic - then we get 100 pieces. Unfortunately a 10x10 square is not possible but Miroslav Vicher has formed a 9x11 rectangle with 99 of the pieces.
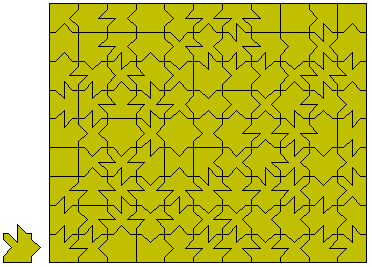
Peter Esser has found some solutions with the order 6 X-ominoes. There are 231 two sided pieces and 336 one sided pieces as shown in the diagrams below.
Here we use two male and two female type edges to get 120 pieces. This 10x12 rectangle was made by Alessandro Fogliati in Aug 2001.
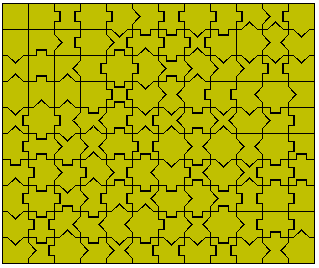

666 pieces = 37x18 rectangle with sinusoidal edge (odd harmonics). Solution by Alessandro Fogliati.

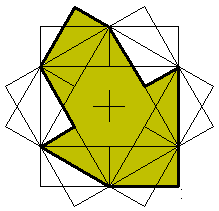
For this puzzle we have a hexagon with edges - neuter, +/- a drafter - giving 1355 pieces. Solution of 1355 pieces by Mark Stubbings inAug 2001.
