There are 54 rhombsliced heptiamonds shown here in a triangle consisting of three congruent parts.
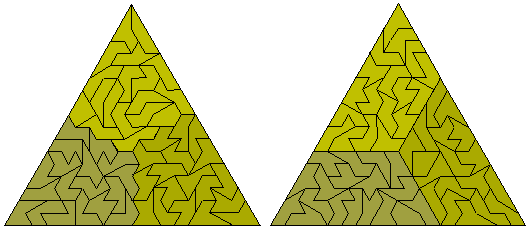
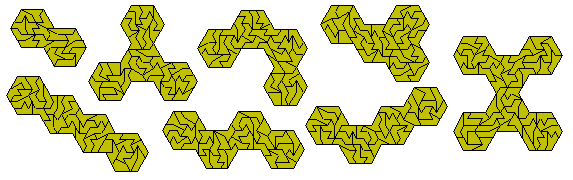
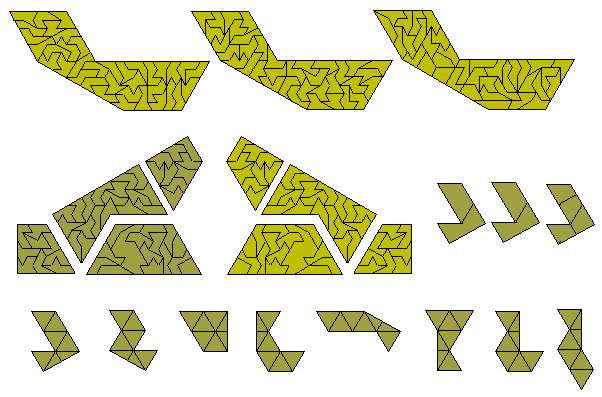
Other two and three congruent part shapes are shown below. The first and fourth figure show the maximum number (12) of edges a convex figure can have and the second has the maximum possible number of symmetries. The final figure shows six congruent figures made from the set.
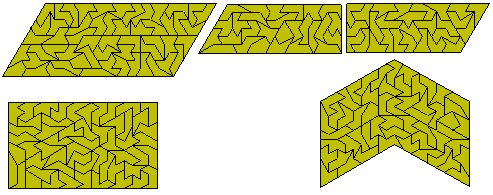
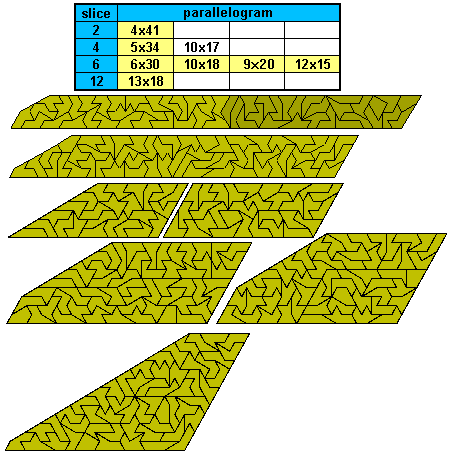
The next figures show the two possible parallelograms the second one consisting of two congruent parts which can be rearranged to form a rectangle or a trapezium. The triangle and the first parallelogram form sextuplications of two of the three tetriamonds. Peter Esser has found a solution to the third one as shown at the bottom right below together with the rectangle at the bottom left.
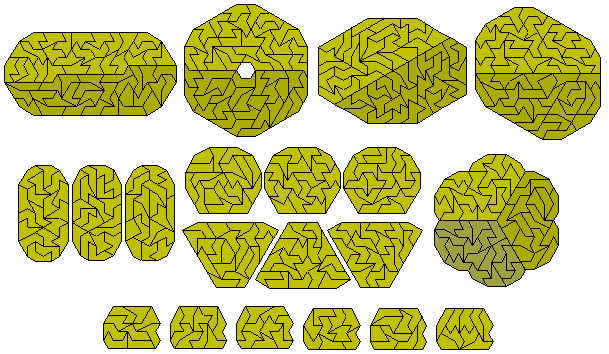
The diagrams above give examples of two, three and six congruent shapes made with the set. Nine congruent might also be possible although very unlikely. Sets of similar shapes are also possible a number of examples being shown here.
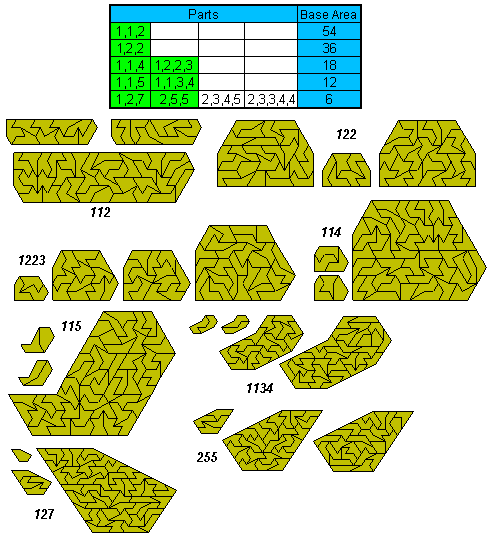
Peter Esser has noted that the total area of the pieces is just sufficient to triplicate an hexahex. His diagrams below provide all solutions. The dihex can be combined with the tetrahexes to form all but one of the solutions. The remaining one is shown at the bottom.
Sliced paralleograms and trapezia are also possible. The first figure below can be used to form either a trapezium or a parallelogram by the reflection of the darker coloured area.
One-sided Rhombsliced Heptiamonds
Peter Esser notes - "Since all rhombsliced heptiamonds aren't symmetric the one-sided set has 108 pieces and you can try to make three sixfold replicas of the hexiamonds and the sliced pieces themselves if there are no 30 degree angles. I have got half of a solution using the two-sided set and then reflected it to get the whole construction."
Peter has also made a hexagon with the one-sided set. Notice that all sides of the hexagon are made up of sliced edges.
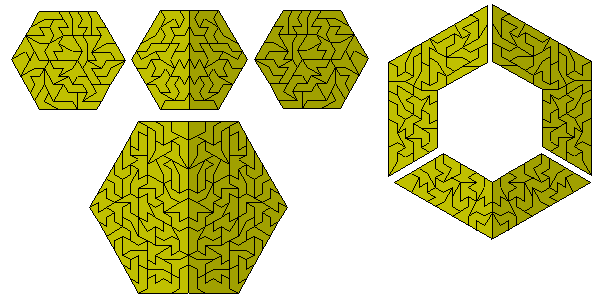
All but three of the hexiamonds can be solved using the three trapezia in the triangle above and reproduced below with the reflected parts.. The remaining three are shown below (the second and fourth of these diagrams is by Peter Esser).
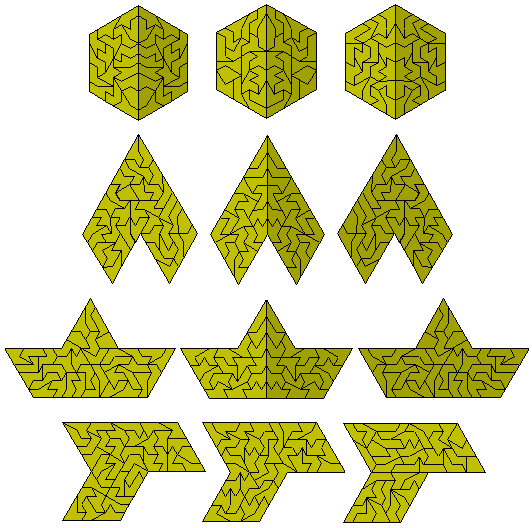
The last solution (the pistol) is the hardest since all the others can be made from two parts using one set of two-sided pieces for each part. Equally as hard is the problem of three replications of each of the pieces. Peter Esser has solved this problem for one piece the first piece below and has also provided the constructions in the rest of the diagram which provide solutions to the eight pieces shown. Peter also notes that 36 pieces cannot be triplicated owing to their having 30° angles and so this leaves seven problems outstanding.
Peter has also solved three of the remaining problems.
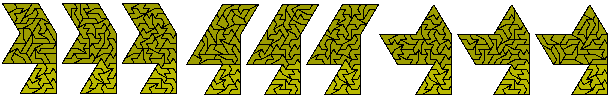
Nine congruent shapes can also be made with this set. The dodecagon below is by Peter Esser.
