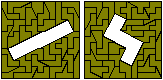
Domsliced Pentominoes
The total area of these shapes is 144 units and a number of rectangles can be made from this set. The diagram below shows all possible rectangles - the 12x12 and 9x16 are by Roel Huisman. Notice that the 4x36, 6x24 and the 8x18 are both made from two smaller rectangles and so also give solutions to 8x18, 12x12 and 9x16 rectangles respectively. Roel has also found three 6x8 rectangles made with the set (figure at the lower right below).

The only other rectangles with area 144 are 2x72 and 3x48 neither of which can be made. It is easy to see that the 2x72 is not possible since a number of the pieces have a width greater than 2. The 3x48 can be shown to be impossible by considering firstly the amount each piece can contribute to the two long edges. This turns out to be exactly 96 which is just the amount required. However, if we now consider how much each piece can contribute to the central row of squares we come up short of the required 48. This proof is thanks to Peter Esser who has also found the three rectangles made with this set shown below.

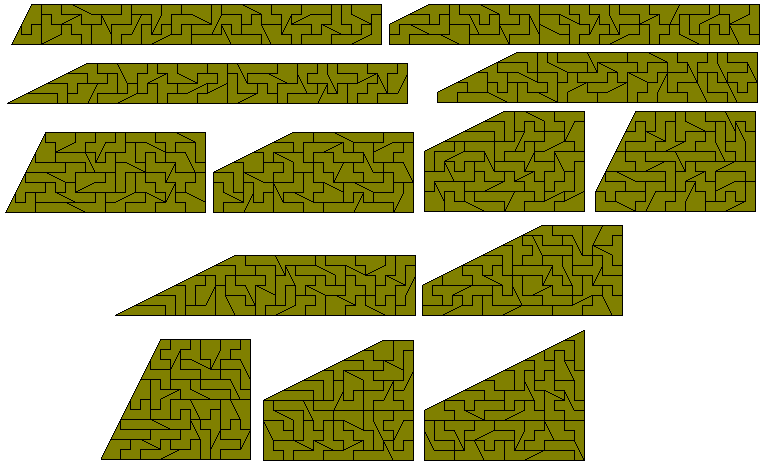
A number of 'sliced rectangle' can also be made with this set. For a single slice there are thirteen possibilities shown below.
It is possible to make two, three or four congruent shapes with this set.
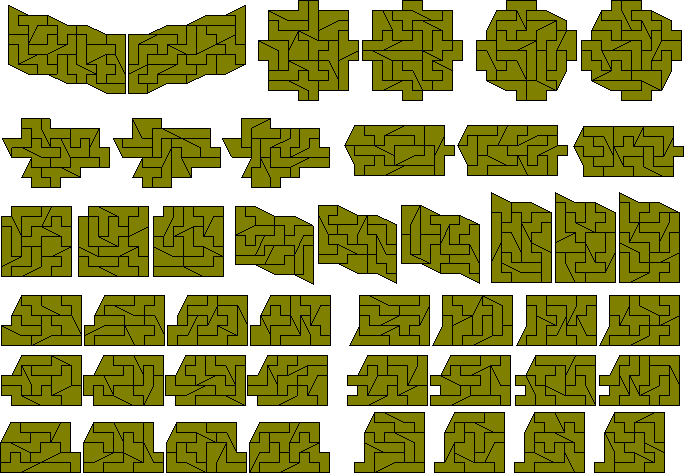
It may be possible to form six congruent pieces with this set but no solution is known. The set can, however, form two sets of three congruent shapes or three sets of two congruent shapes.
![]()
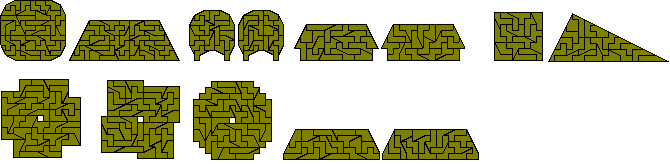
A number of other constructions by Roel Huisman are shown here.

There are many other figures which are possible such as the examples below. Notice that a number of these constructions are made from two congruent parts.
It is possible to make six-fold replicas of all the pieces (see Roel Huisman's site for the remaining solutions).

One of the hardest constructions to make with the domsliced pentominoes is one where the border consists entirely of sliced edges. Only one non-symmetrical figure is known. Two symmetrical shapes which might provide solutions are also shown here.
There is also a number of similar hole constructions which can be made.

Peter Esser has found two solutions to the problem of forming a rectangle with a hole in the shape of a pentomino.