Polyforms derived from combinations of other n-forms.
![]()
Polytrominoes
Polytrominoes are combinations of trominoes. The figure below shows the 29 ditrominoes firstly in the only possible rectangle the 6x29.
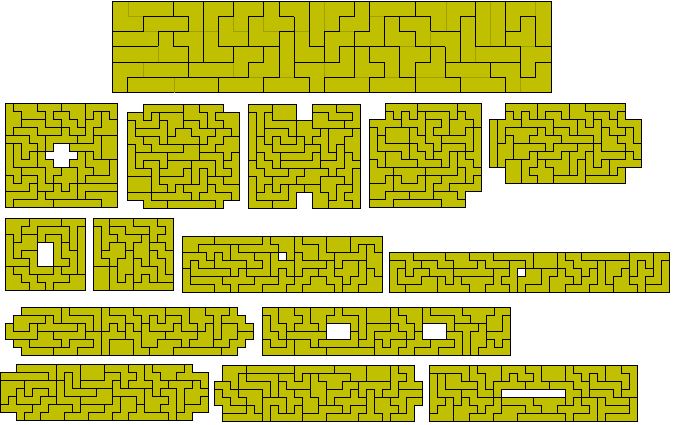
The one-sided set has 51 pieces but, since there is an odd number of unbalanced pieces, no rectangle can be made with the set.

Notice that there are two types of tromino used and other, smaller sets could be produced if we were to look at specific combinations - two trominoes of the same type or one of each type as in this construction.
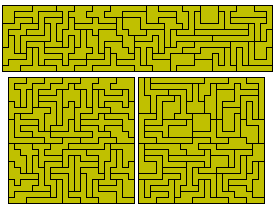
Ditetrominoes
If we join two L tetrominoes then we get a set of 64 pieces one of which has a hole. Patrick Hamlyn has managed to pack the remaining 63 pieces into three 8x21 rectangles.
Polydiamonds are sets formed from the joining of diamonds (two joined equilateral triangles). The n-diamonds are subsets of the 2n-iamonds. For constructions with these see Miroslav Vicher's site.
Brendan Owen has made some constructions with the one sided tridiamonds and the tetradiamonds.
With the tetradiamonds there is one piece which can be formed in two distict ways. We normally only use one piece in any construction. For the pentadiamonds there are ten such pieces.
If we join dicubes we form subsets of the 2n-cubes. There are six didicubes with a total volume of 24 unit cubes (see the figure below which also shows how they can for a 2x3x4 box). Joining three dicubes gives us the 103 tridicubes made up of solid versions of the 23 tridominoes and a further 80 three dimensional pieces giving a total volume of 618 unit cubes. If we use one of each mirror pair then we get a set of 67 pieces. Since both 103 and 67 are primes the only possible boxes would be 2x3x103 or 2x3x67.
The 2x3x103 is possible by combining the 2x3x23 box made with the solid tridominoes and this set of 16 2x3x5 boxes found by Brendan Owen.
Note: With all the of the above there is a problem of choice as to whether we consider different combinations producing the same shape as different on not (see diagram below for examples).

Mostly we should consider these to be the same but they could be considered as distinct. If we were to consider these as different for the tridominoes we should get 26 pieces as shown below in two 6x13 rectangles. Also shown here is the one-sided set of 45 pieces in five 6x9 rectangles and other sets of rectangles.
Similarly with the ditrominoes there are two pieces which can be formed in two different ways. The resulting set of 31 pieces has an unbalanced colouring so no rectangle is possible. The set can, however, form a number of symmetrical shapes.
With the one-sided set we get 54 pieces but these also can only form unbalanced figures.