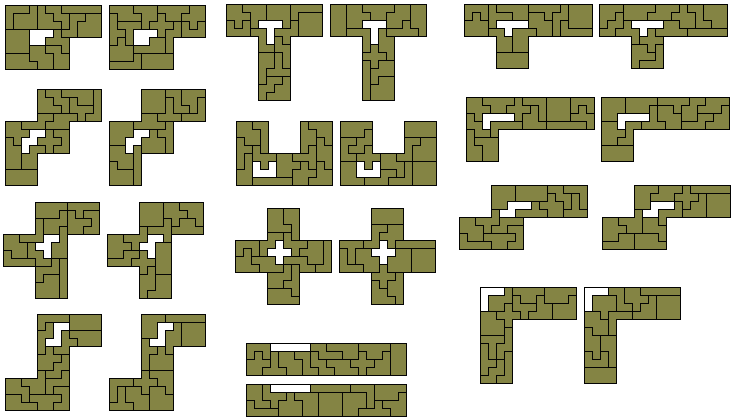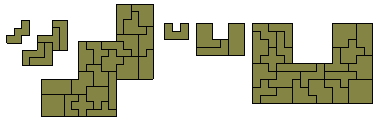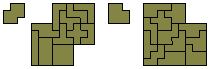

A variety of problems with this set is shown below.
The construction below can be used to make pentuplications
of all 35 hexominoes.
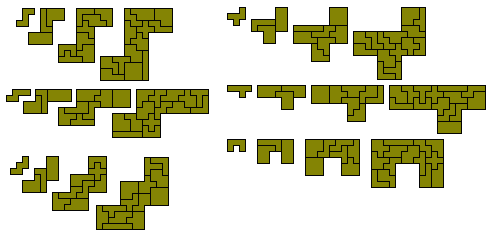
Quadruplication of a dekomino with a hole in the shape of
the dekomino.
Ttwo quadruplicated pentominoes with a hole in the shape
of the pentomino.
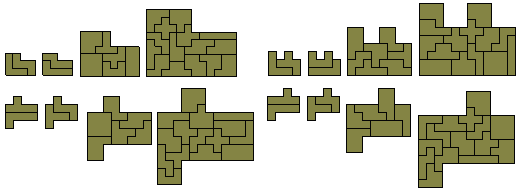
1-2-3-4 problem. Take one of the pentominoes in the set
and with the rest make double- triple- and quadruple-sized replicas.
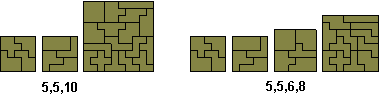
1-1-2-3 problem. Create an area of 10 square units, produce
a copy, a duplication and a triplication.
3-4 problem. With the whole set produce simultaneous triplication
and quadruplication of an hexomino.
1-2-5 problem - take one pentomino from the set and then
with the remaining pieces create double and fivefold replicas.
7-8 problem. Remove one heptomino and one octomino from
the set and with the remaining pieces makes simultaneous triplications of
both pieces.
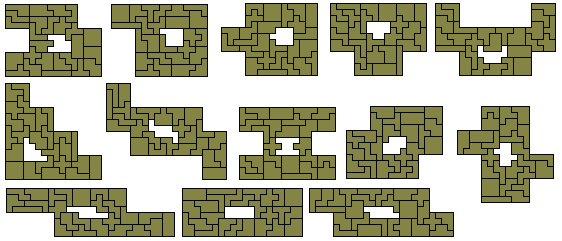
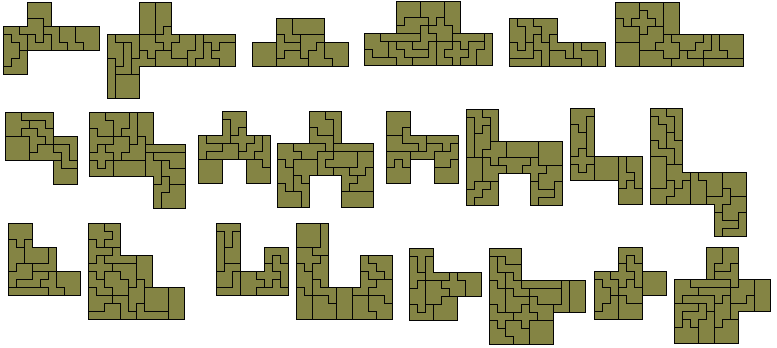
Three twins problem - create three sets of pairs of congruent
shapes
Two triplets problem - create two sets of three congruent
shapes
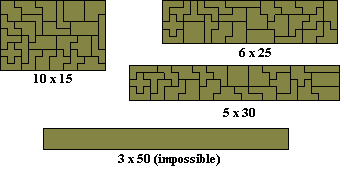
Quintuplets - create 5 congruent shapes each with area 30
Sextuplets - create 6 congruent shapes each with area 25
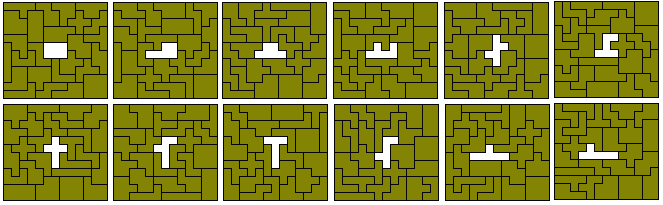
Make two 9x9 squares with a hole in each in the shape of
an hexomino
Make a 12x13 rectangle with a hole in the shape of an hexomino.
All 35 problems are likely to be possible.
Sets of squares

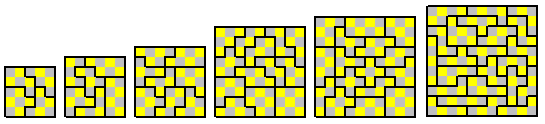
The two-sided same chequered set consists of 48 pieces with
a total area of 286.
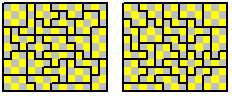
The two-sided opposite chequered set consists of 38 pieces
with a total area of 227.

The one-sided chequered set consists of 70 pieces with a
total area of 412.