If we allow only translations for pieces then we get 2 dominoes, 6 trominoes, 19 tetrominoes etc. Iwan Jensen has found the numbers of fixed polyominoes up to order 56. The six fixed trominoes can form a 3x6 rectangle as shown below.
![]()
Mike Reid has shown that the 19 fixed tetrominoes cannot form a rectangle although a number of constructions can be made.

Patrick Hamlyn has found the following rectangles with the 63 fixed pentominoes. In each solution no congruent pieces touch each other and each rectangle is made up of a number of smaller (congruent) rectangles.


Brendan Owen has found nine 5x7 rectangles with this set.

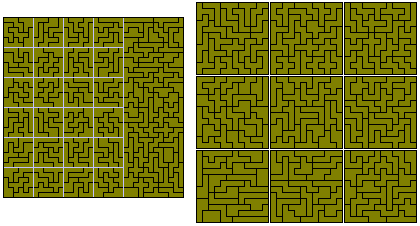
Brendan has also formed the 216 fixed hexominoes into a 36x36 square made up of a 12x36 rectangle and twenty four 6x6 squares. Another way of forming the square is by means of the nine 12x12 squares shown at the right.
If we allow 180° rotations of pieces we get what Peter Esser calls polarised sets of pieces. There are 35 pentominoes in this set which can form 5x35 and 7x25 rectangles. The set can also form fivefold replications of the heptominoes. Three examples of this are shown together with sets of constructions which can be used to make any of the 108 heptominoes.

There are 120 polarised hexominoes which can make three, four, five, six, eight and ten congruent rectangles

The above refer to one-sided sets. For the two sided pentominoes there is also a number of possibilities that Peter has introduced. See Chequered Polyforms for other variations.
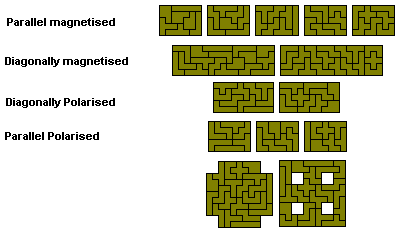
The parallel polarised set can also be considered as PolyRects (rectangles)