Of the pentominoes, one (the U) has an indentation while the remaining eleven pieces have none. These we can call convex pentominoes. A more precise definition would be -A convex polyomino is one whose perimeter is that of its bounding rectangle.The table below shows the number of convex n-ominoes for n = 5 to 8.
This set is unbalanced as to chessboard colouring.
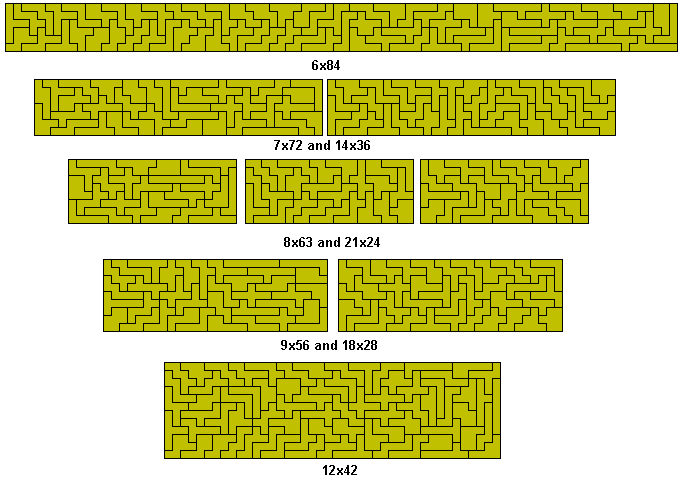
A number of rectangles are possible with this set - 6x84, 7x72, 8x63, 9x56, 12x42, 14x36, 18x28 and 21x24.
The remaining 36 heptominoes are shown here.

If we omit the piece with a hole, the remaining pieces can form a 7x35 rectangle.
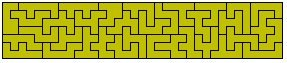
This set is unbalanced as to chessboard colouring.
![]()
Of the remaining 178 octominoes 6 have holes and the remaining pieces can form four 8x43 rectangles.
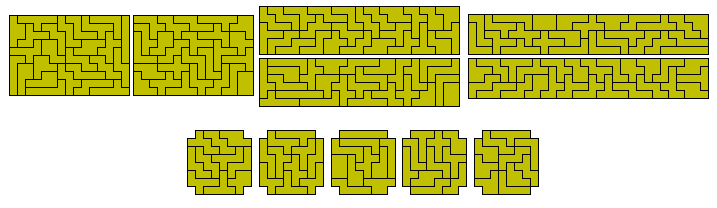
5x60, 6x50, 10x30, 12x25 and 15x20 are possible as shown by the pairs of rectangles formed by the set below. Maximum edging is 136 with an extra 14 possible with the pieces forming the corners. A 4x75 rectangle would need 158 edges and so cannot be made. With five congruent rectangles the maximum edging available is 172 which might allow us to make five 6x10 (edging 160) or 5x12 (edging 170) rectangles although the latter would have few, if any, solutions. The bottom figure below shows five congruent figures.

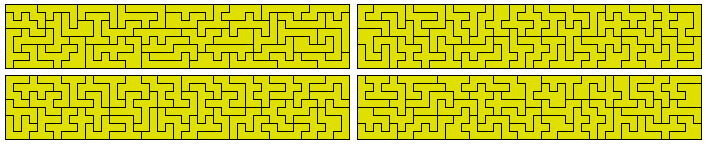
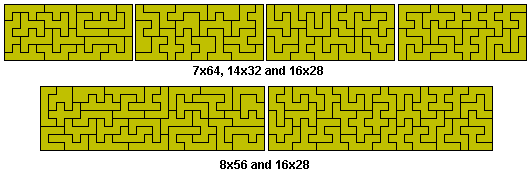
Of the 65 remining heptominoes one has a hole. Omiiting this piece we get a set of 64 pieces which can form 7x54, 8x28, 14x32 and 16x28 rectangles. A 4x112 may also be possible.
There are 63 one-sided heptominoes which are not convex one of which has a hole

Omitting the piece with a hole the remaining 62 pieces can form two 7x31 rectangles.
