The 8 pentominoes (F, N, T, U, V, W, X, Z) which cannot form rectangles by themselves do forms rectangles with one other pentomino. The question asked here is - which of these pentominoes form rectangles in which they completely dominate the other pentomnio in the sense that the ratio of one to the other can be made arbitrarily large. Some example are given below.
![]()
This diagram shows a construction of a 4x10 rectangle with U and N pentominoes. If the centre section is used k times then we shall have 4k+2 Ns and just 2 Us. Thus the N completely dominates the U and could be said to be almost rectifiable.
This next diagram show, similarly, that the N completely dominates the T.
![]()
Here the F is seen to be almost rectifiable completely dominating the U.
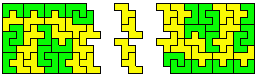
In this diagram the F and V are show to able to completely dominate each other.
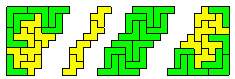
And here the W is shown to be almost rectifiable.
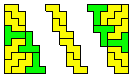
In the diagram above the two Ys at the join of the two 5x5 squares can be replaced with two Xs (move the mouse over the diagram).
Now if we join k 5x5 squares to form a new square of side 5k (see above where k = 4) and then change adjoining Ys to Xs we shall get a square formed with 4k Ys and 5k2 - 4k Xs which will give a ratio (5k/4 - 1):1 of Xs to Ys and since this ratio can be made as large as we like the X is also almost rectifiable.
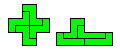
The final diagram shows double sized X and Y pentominoes formed from Z and L pentominoes. Noting that the X is formed only by Zs we see that of these pieces are joined to form the previous diagram where the X is almost rectifiable then we see that the Z is also almost rectifiable.
Finally the diagram below shows two examples of almost rectifiable hexominoes.

