Enhanced Sets of Pentominoes
Enhanced Sets of Pentominoes
If we take a set of pentominoes and add n copies of one of the pieces, rectangles can be made with this set for given values of n.
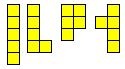
The I can be added any number of times to a 5x12 rectangle. The L and P both can form a 2x5 rectangle which together with the upper constructions below give solutions for all n. Finally the Y forms a 5x10 rectangle and so with the lower constructions it can be seen that the problem is possible for all n.
![]()
Rectangles are possible for all values of n.
![]()
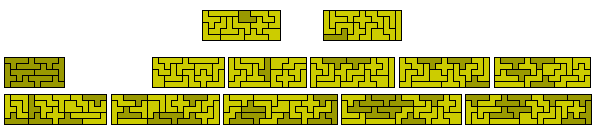
The N has the most complex set of solutions and these are shown on a separate page.
![]()
This is possible for n < 17 and n = 18, 20. It is likely, although not proved, that values of n of the form p-12 for n>11 are not possible.
![]()
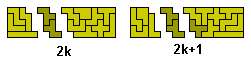
Mike Reid has also provided the following analysis showing that there must be a maximum value of n for which the U's can form a rectangle with the pentominoes.
![]()
Possible for all n
![]()
Possible for all n
![]()
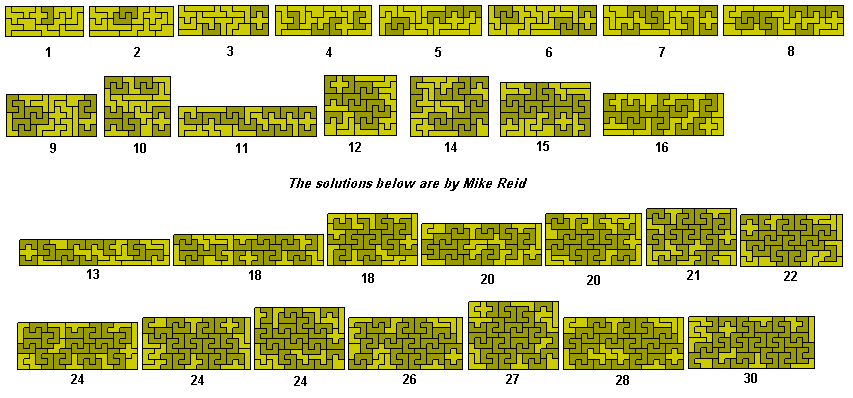
Mike Reid has shown that the above are the only possibilities.

![]()
The solutions for 14, 15 , 16, 18 and 21 are by Patrick Hamlyn who has also found that n=17 is impossible as is any n of the form prime - 12.