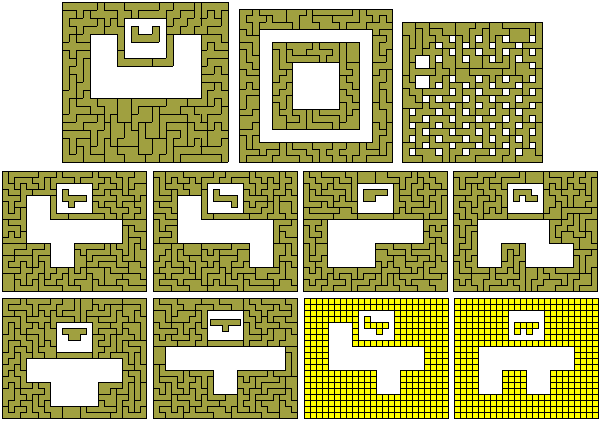
Similar Hole Constructions with the Sixty One-Sided Hexominoes

The possible constructions are based on factorisations of 360 (the total area of the pieces) in the form (a² - b²) x cd. Such a factorisation will produce d copies of an a-fold replica of a c-omino with a b-fold similar hole.

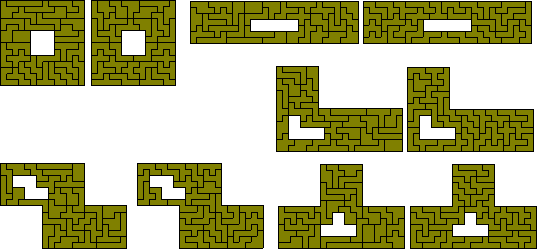
If d = 1 we have a number of possibilities. The nested squares figure is by Roel Huismann and the figure at the top left is by Mike Reid.

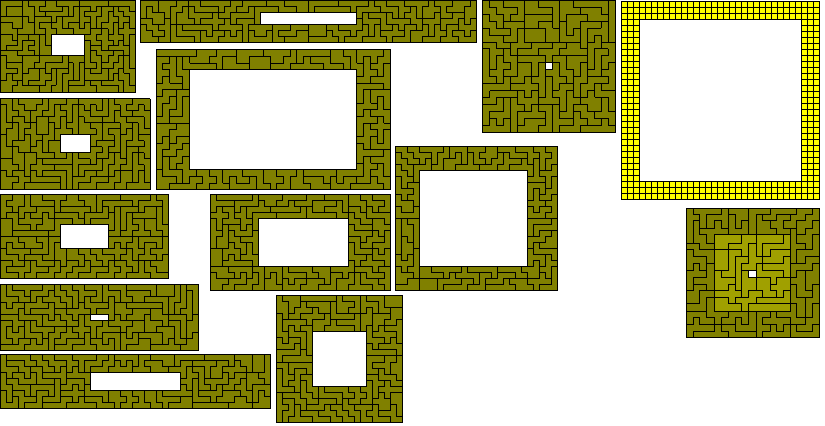
The following data are based on the various factorisations. (Some non-rectangular solutions for d=1 are also shown)

(a) (2² - 1²) x120

(b) (3² - 2²) x 72 (solution by Peter Esser)

(c) (3² - 1²) x 45

Three triplicated 15-ominoes

Five triplicated enneominoes

(d) (5² - 4²) x 40

(e) (4² - 2²) x 30

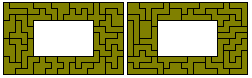
(f) (4² - 1²) x 24

Two quadruplicated 12-ominoes

Three quadruplicated octominoes

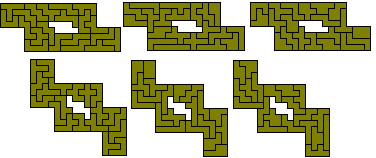
Four quadruplicated hexominoes - 35 problems (61 if we consider solutions in mirror pairs as in some solutions below).

Six quadruplicated copies of tetromino - five problems with four solved (the last two are by Patrick Hamlyn).

(g) (6² - 4²) x18

(h) (5² - 1²) x 15

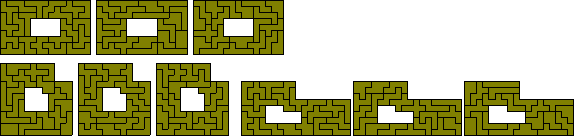
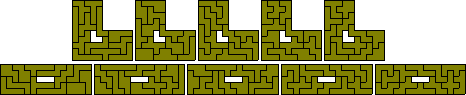
Three pentuplicated pentominoes - 12 problems all solved (the last six by Roel Huismann).

Five pentuplicated trominoes - two problems with both solved.

(i) (7² - 5² ) x 15

(j) (10² - 8²) x 10

(k) (7² - 3²) x 9

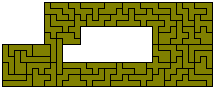
(l) (11² - 9²) x 9

(m) (7² - 2²) x 8

Four septuplicated dominoes with a duplicated domino hole.

Two septuplicated copies of a tetromino with a duplicated tetromino hole - 5 problems all of which are solved.

(n) (8² - 2²) x 6

Three octuplicated dominoes with a duplicated domino hole.

Two octuplicated trominoes with a duplicated tromino hole.

(o) (16² - 14²) x 6

(p) (11² - 1²) x 3

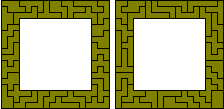
Three 11x11 squares with single hole

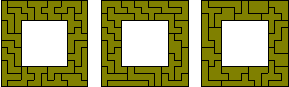
(q) (13² - 7²) x 3

Three 13x13 squares with a 7x7 square hole (solution by Patrick Hamlyn).

(r) (17² - 13²) x 3

(s) (31² - 29²) x 3

(t) (14² - 4²) x 2

(u) (46² - 44²) x 2

Mike Reid (left figure) and Patrick Hamlyn have made some interesting variations on the similar hole theme. There are other possible variations to Mike's construction as shown at the bottom (the first two solutions are by Roel Huisman). The two at the bottom right are not possible owing to their being unbalanced.