Les tables suivante ont les nombres (a) des polyminos d'une région donnée, A, et périmètre, p, et (b) les régions totales de ces ensembles de morceaux. Ces tables ont été fournies par Brendan Owen.
Les tables suivante ont les nombres (a) des polyminos d'une région donnée, A, et périmètre, p, et (b) les régions totales de ces ensembles de morceaux. Ces tables ont été fournies par Brendan Owen.
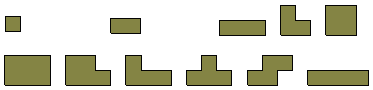
Les polyminos de périmètres 4, 6 , 8 et 10
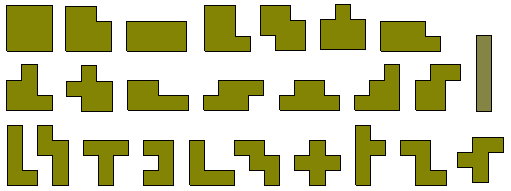
Les 25 polyminos de périmètre 12
Les six polyminos de périmètre 10 a une aire totale de 27 carrés et put construire quelques constructions comme les trois en dessous.Le 25 polyminos de périmètre 12 a une région totale de 150 unités. A grand nombre de problèmes est disponible avec cet ensemble comme en dessous. Comme cette ensemble nous n'avons pas de problèmes de la parité et ily a est une grande variété de constructions multiples dans qui les régions de le parties ne sont pas arrangées comme un multiple de quelque nombre fixe.
Brendan Owen a trouvé les 86 polyminos de périmètre 14.
Notez: Livio Zucca a étendu l'idée de isoperimetry avec son Polyedges.
Il y a 86 polyminos de périmètre 14 qui couvrent une région de 641 carré.
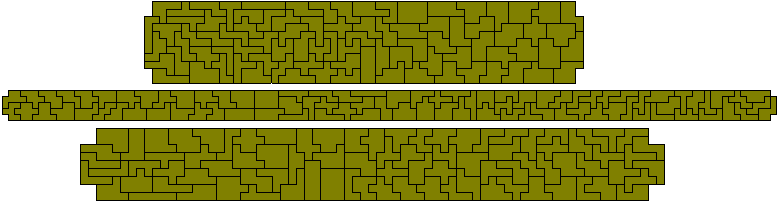
Malheureusement pas de rectangles peuvent être faits mais si nous utilisons un des enneaminos deux fois un 13x50 rectangle peut être fait. Ce donne un total de 9 problèmes un de qui est montré en dessous.

De la même façon si nous avons utilisé un octamino deux fois c'est possible de former un 11x59 rectangle et un dekamino deux fois on peut former un 7x93 rectangle. Aussi si nous omettons le 3x4 rectangle de l'ensemble qui nous pouvons former un 17x37 rectangle.
Probablement le problème le plus difficile pour cet ensemble est former des carrés simultanés. Ces solutions ont été produites par ordinateurpar utiliser Gerard's Universal Polyomino Solver. Le premier a pris sous 30 minutes, le deuxième environ 20 et le troisième environ 15 bien.
The above shows solutions with 9, 10, 11and 12 squares. The question naturally arises - what is the maximum number of squares which can be made with this set? There are over 2000 ways of expressing 641 as the sum of squares even when we reject any with a 1, 2 or 3 and only allow a maximum of four 4s which is all the set can produce.
L'au-dessus montre solutions avec 9, 10, 11 et 12 carrés. La question s'élève naturellement - ce qui est le maximum compte de carrés qui peut être fait avec cet ensemble? Il y a sur 2000 chemins d'exprimer 641 comme la somme de carrés même quand nous repoussons tout avec un 1, 2 ou 3 et seul permet un maximum de quatre 4s qui est tout l'ensemble peut produire.
Patrick Hamlyn a trouvé 15 carrés.
Si, cependant, nous cherchons des carrés qui sont tout différent alors nous trouvons le y a seulement 19 ensembles possibles de carrés.
Le polyominos unilatérals de périmètre 14 peut former un 12 x 97 rectangle. Cette solution a été produit par utiliser Gerard's Universal Polyomino Solver qui a obtenu la solution dans appuie environ 20 après un peu d'organisation prudente.
Il y a un aussi un grand nombre d'ensembles de carrés qui peuvent être faits avec cet ensemble. Exemples avec 5, 13 et 17 rendent carrés sont monte ici.
On peut chercher aussi ensembles de morceaux avec le même périmètre et région. Par exemple le 21 heptaminos de périmètre 14 peut former un 7x21 rectangle et plusieurs autre constructions. Brendan Owen a montré ce trois 7x7 rend carré ne peut pas être fait avec cet ensemble un résultat qui a été confirmé par Patrick Hamlyn. Les deux Brendan et Patrick ont utilisé un ordinateur pour chercher un solution mais Mike Reid a produit une preuve déductive.