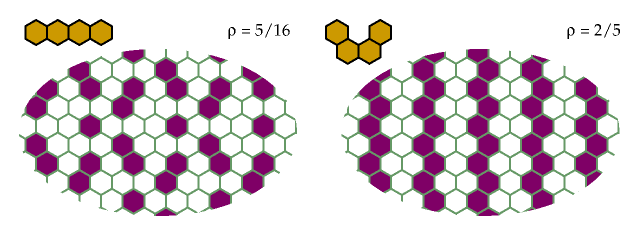Polyhex Exclusion
Introduction
In the 1950s, Solomon W. Golomb investigated the question:
how few cells can you remove from the plane
to exclude the shape of a given polyomino?
Here I investigate into the related question:
how few cells can you remove from the plane
to exclude the shape of a given polyhex?
Dihex
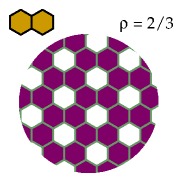
The dihex is hard to exclude!
You must remove at least 2/3 of the cells:
Trihexes
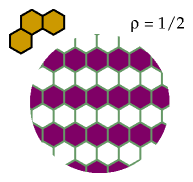
To exclude the bent trihex you can remove half the cells.
If you have a better exclusion, please let me know.
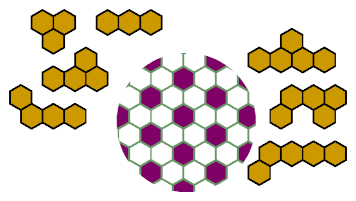
These trihexes and tetrahexes are excluded minimally,
and the pentahexes probably are too:
 |
| ρ = 1/3 |
Tetrahexes
These tetrahex exclusions are minimal:
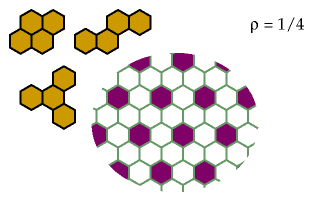
These are probably minimal:
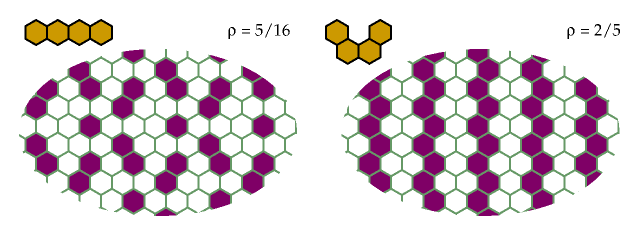
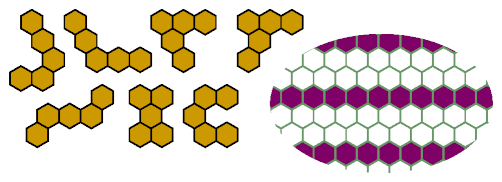
Pentahexes
For the I pentahex, see under General Results.
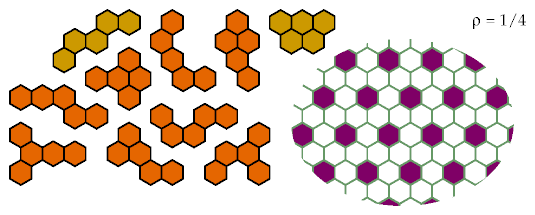
This pattern is minimal for excluding the orange pentahexes,
and probably minimal for the others.
See below for proofs for the orange pentahexes.
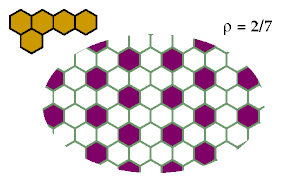
This pattern may be minimal for excluding the Y pentahex:
This pattern is probably minimal for exluding these pentahexes:
 |
| ρ = 1/3 |
Hexahexes
This exclusion for the straight hexahex is probably minimal:
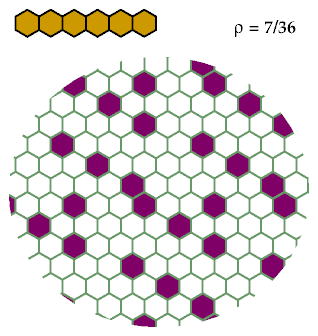
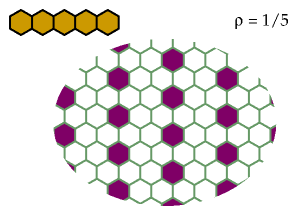
A straight polyhex of odd order n can be excluded with 1/n
holes.
Here is an example for n=5:
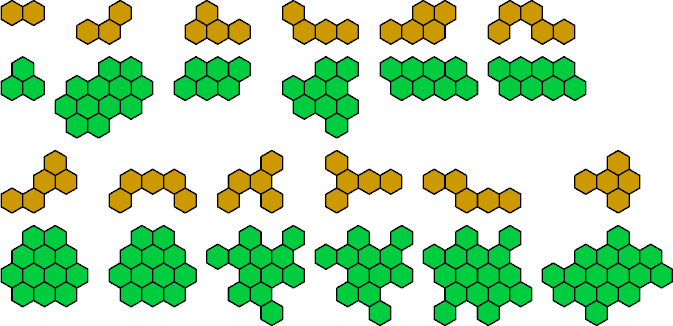
Optimality Proofs
This diagram illustrates the optimality of some of the exclusions
with more than 1/n holes.
Every green figure tiles the plane.
Last revised 2018-05-30.
Back to Polyform Exclusion, Equalization, Variegation, and Integration
< Polyform Curiosities
Col. George Sicherman
[ HOME
| MAIL
]