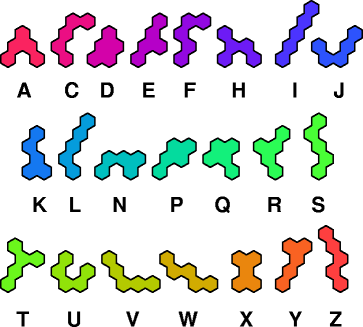
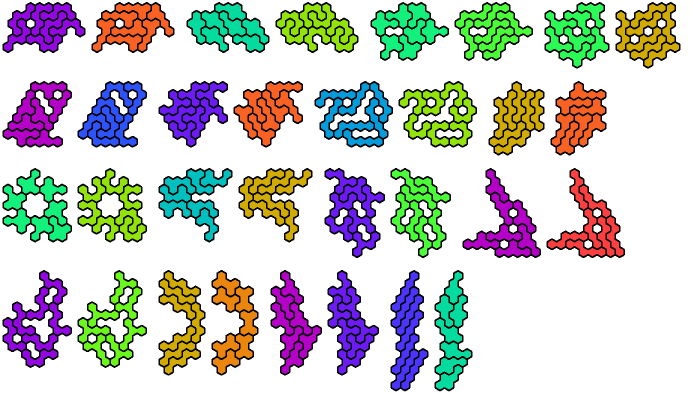
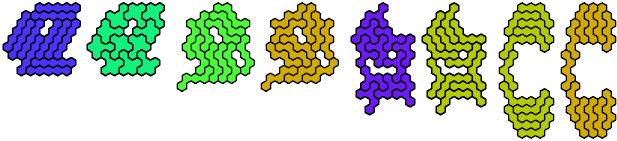
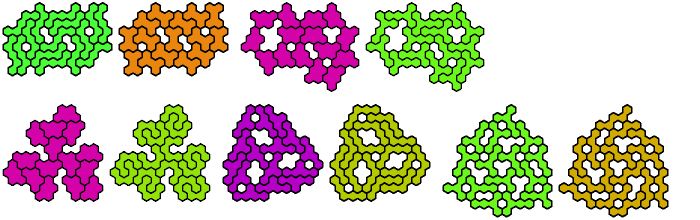
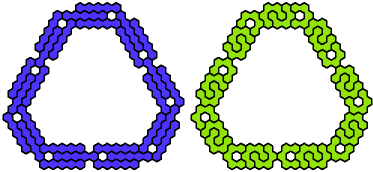
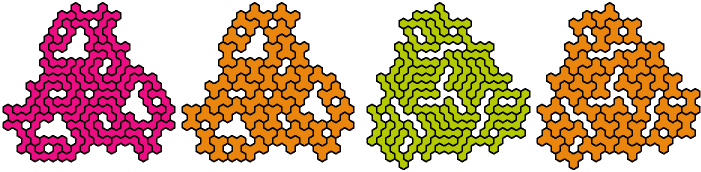
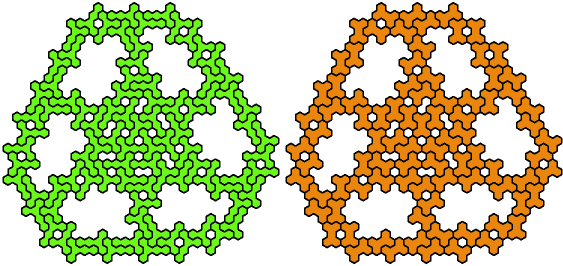
Pentahex Compatibility shows minimal known compatibility figures for pairs of pentahexes. Here are minimal known compatibility figures with an odd number of tiles.
For odd compatibility figures for pairs of pentominoes, see Livio Zucca's Pentomino Odd Pairs.
A convenient set of acrylic pentahexes (and smaller polyhexes) is available from Kadon Enterprises as Hexnut.

In the table below, green figures denote solutions that are minimal even without the condition that the number of tiles be odd.
| A | C | D | E | F | H | I | J | K | L | N | P | Q | R | S | T | U | V | W | X | Y | Z | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | * | 9 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 9 | 13 | 9 | 3 | 9 | 3 | 3 | 3 |
| C | 9 | * | 3 | 3 | 3 | 3 | 9 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 39 | 3 | 3 |
| D | 3 | 3 | * | 3 | 3 | 3 | 5 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 15 | 15 | 3 | 5 | 3 | 3 | 3 |
| E | 3 | 3 | 3 | * | 3 | 7 | 3 | 7 | 3 | 3 | 3 | 3 | 3 | 3 | 9 | 3 | 3 | 15 | 3 | 3 | 3 | 7 |
| F | 3 | 3 | 3 | 3 | * | 3 | 9 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 7 | 3 | 13 | 3 | 9 | 7 | 3 |
| H | 3 | 3 | 3 | 7 | 3 | * | 13 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 7 | 3 | 3 | 11 | 3 | 3 | 7 | 3 |
| I | 3 | 9 | 5 | 3 | 9 | 13 | * | 3 | 13 | 3 | 3 | 7 | 11 | 3 | 5 | ? | 27 | 3 | 5 | 35 | 3 | 5 |
| J | 3 | 3 | 3 | 7 | 3 | 3 | 3 | * | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
| K | 3 | 3 | 3 | 3 | 3 | 3 | 13 | 3 | * | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
| L | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | * | 3 | 3 | 3 | 3 | 3 | 3 | 7 | 3 | 3 | 13 | 3 | 3 |
| N | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | * | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 7 | 3 | 3 | 3 |
| P | 3 | 3 | 3 | 3 | 3 | 3 | 7 | 3 | 3 | 3 | 3 | * | 3 | 3 | 3 | 9 | 7 | 3 | 3 | 3 | 3 | 3 |
| Q | 3 | 3 | 3 | 3 | 3 | 3 | 11 | 3 | 3 | 3 | 3 | 3 | * | 3 | 7 | 3 | 7 | 9 | 3 | 3 | 3 | 5 |
| R | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | * | 3 | 3 | 3 | 3 | 7 | 3 | 3 | 3 |
| S | 9 | 3 | 3 | 9 | 3 | 7 | 5 | 3 | 3 | 3 | 3 | 3 | 7 | 3 | * | 3 | 3 | 3 | 11 | 15 | 3 | 3 |
| T | 13 | 3 | 15 | 3 | 7 | 3 | ? | 3 | 3 | 3 | 3 | 9 | 3 | 3 | 3 | * | 3 | 3 | 15 | 87 | 3 | 3 |
| U | 9 | 3 | 15 | 3 | 3 | 3 | 27 | 3 | 3 | 7 | 3 | 7 | 7 | 3 | 3 | 3 | * | 9 | 9 | 81 | 9 | 3 |
| V | 3 | 3 | 3 | 15 | 13 | 11 | 3 | 3 | 3 | 3 | 3 | 3 | 9 | 3 | 3 | 3 | 9 | * | 11 | 39 | 3 | 3 |
| W | 9 | 3 | 5 | 3 | 3 | 3 | 5 | 3 | 3 | 3 | 7 | 3 | 3 | 7 | 11 | 15 | 9 | 11 | * | 7 | 7 | 3 |
| X | 3 | 39 | 3 | 3 | 9 | 3 | 35 | 3 | 3 | 13 | 3 | 3 | 3 | 3 | 15 | 87 | 81 | 39 | 7 | * | 3 | 9 |
| Y | 3 | 3 | 3 | 3 | 7 | 7 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 9 | 3 | 7 | 3 | * | 3 |
| Z | 3 | 3 | 3 | 7 | 3 | 3 | 5 | 3 | 3 | 3 | 3 | 3 | 5 | 3 | 3 | 3 | 3 | 3 | 3 | 9 | 3 | * |







Last revised 2023-05-07.