Zucca's Challenge Problem for Tetrahexes
Livio Zucca's
Tetrominoes
Challenge Page challenges you to find plane regions
that can be tiled with each of a given set of tetrominoes and no others.
Here I show solutions to the corresponding
problem for tetrahexes.
If you have a smaller solution for any of these sets, please
let me know.
For extrominoes, see
Zucca's Challenge Problem for Extrominoes.
For polyiamonds, see
Zucca's Challenge Problem for Polyiamonds.
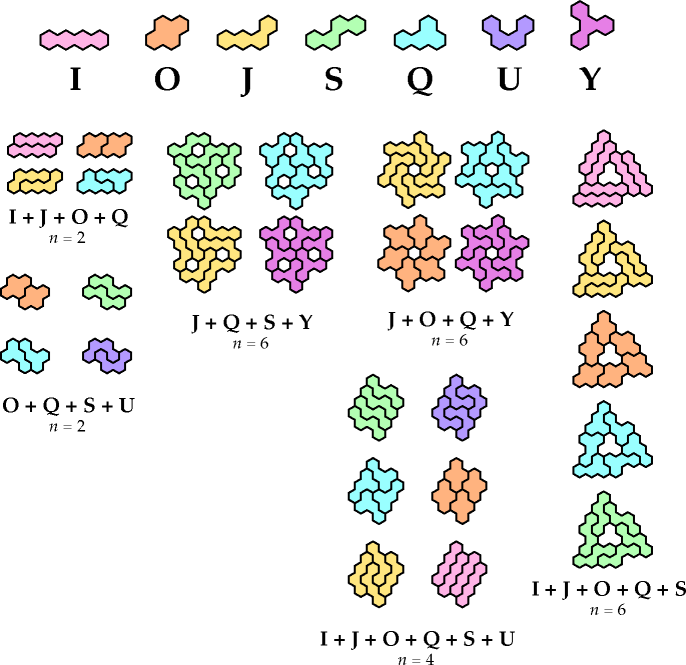
Solutions
There are 7 tetrahexes, so a complete solution for
Zucca's problem for tetrahexes has 120 cases!
That's too many for me.
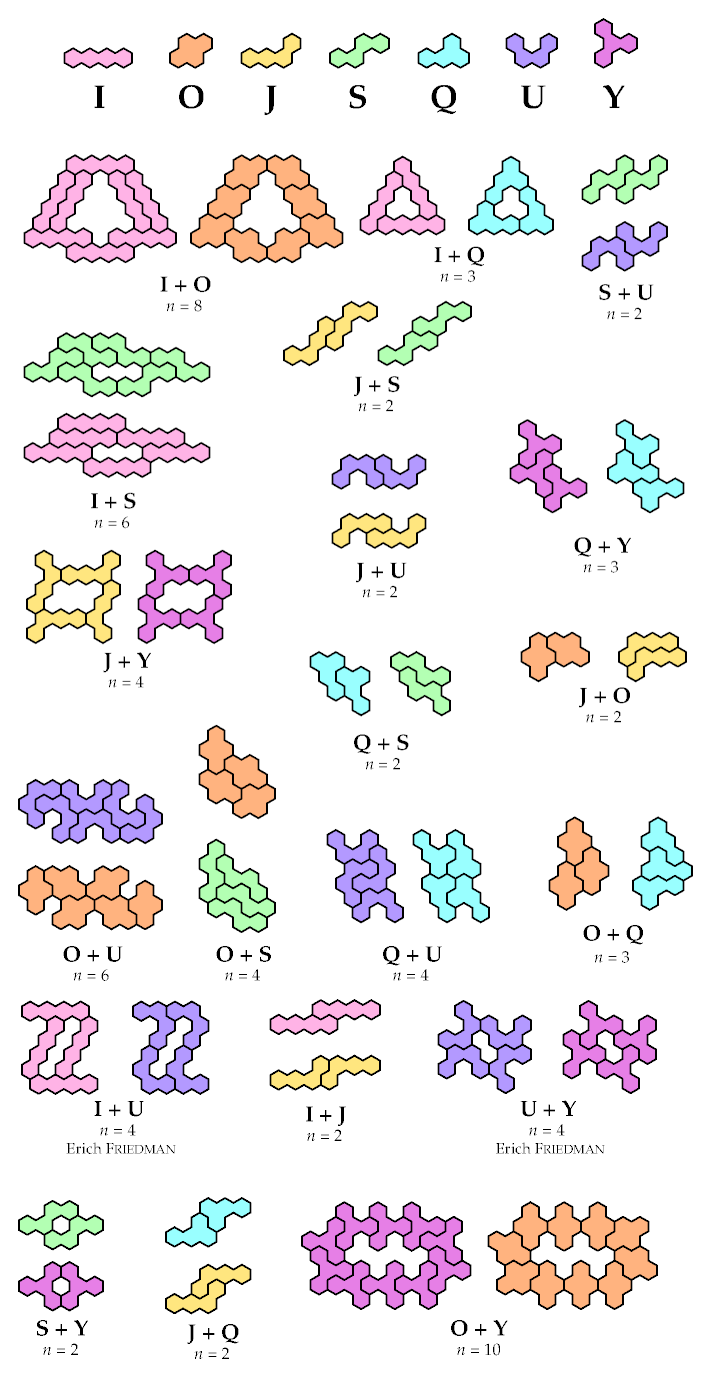
Here are solutions for all the pairs but one.
They may not be minimal.
Thanks to Dr. Friedman for improving on some of my original results.
Pairs
Triplets
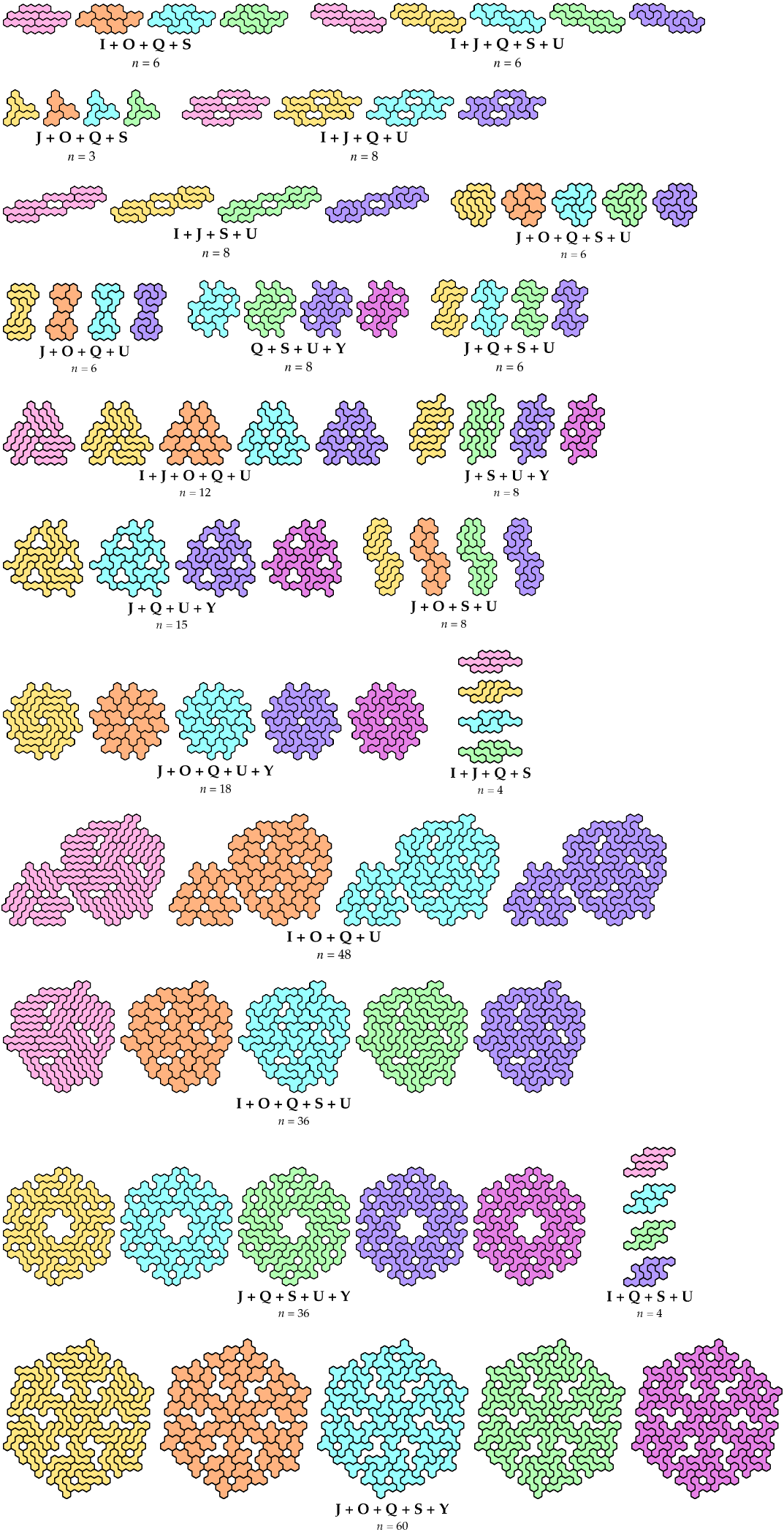
And here, by courtesy of Dr. Friedman or me or both, are some solutions
for sets of three or more:
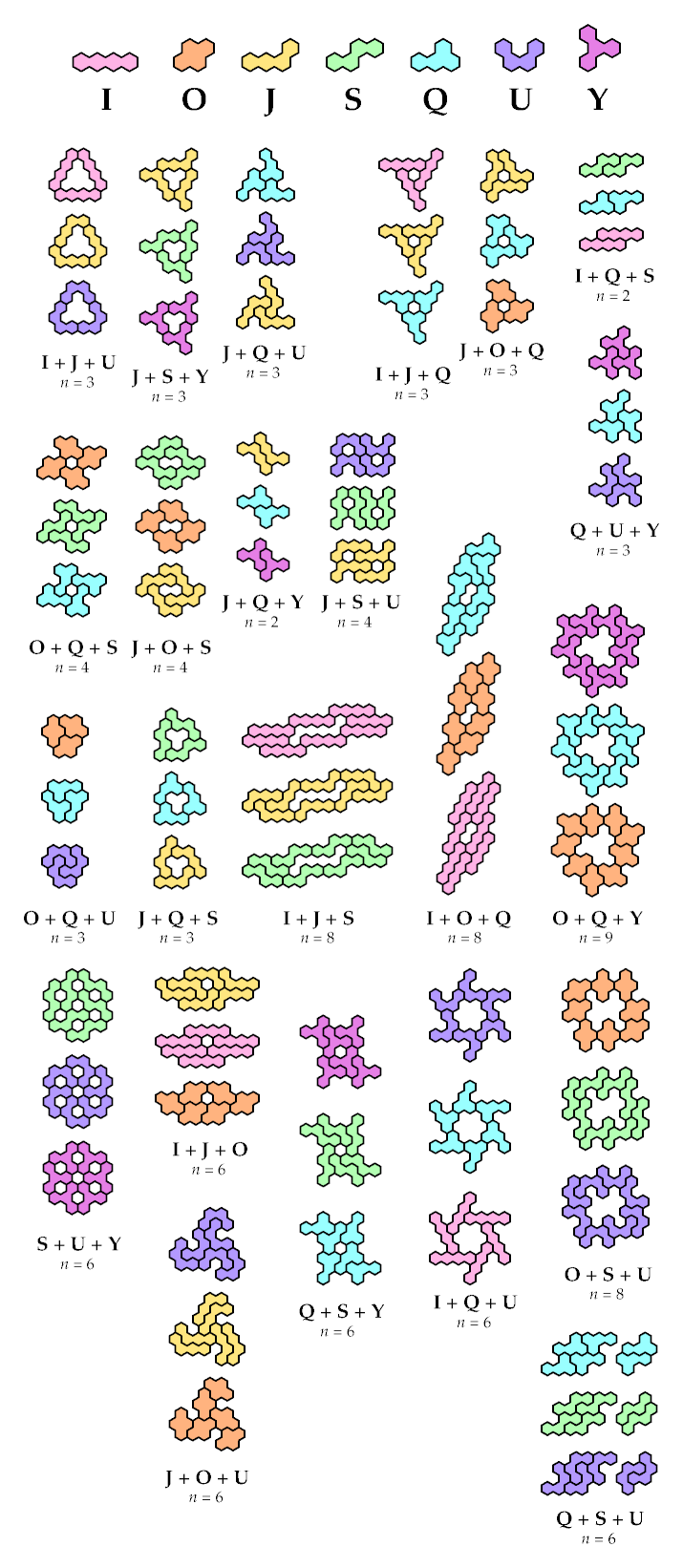

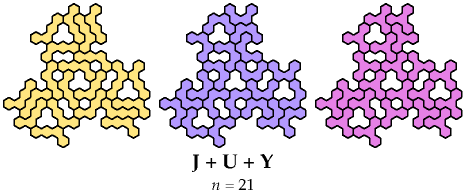
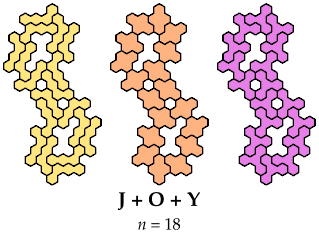
Bigger Sets
Last revised 2018-06-02.
Back to Multiple Compatibility
<
Polyform Compatibility
<
Polyform Curiosities
Col. George Sicherman
[ HOME
| MAIL
]







