

For similar or scaled tetrads, see Scaled Polyomino Tetrads.
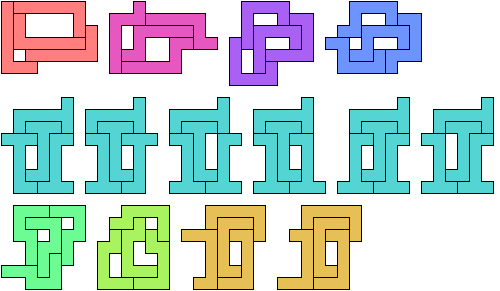
The fifth tetrad was reported by Olexandr Ravsky in 2005.

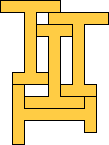
The smallest tetrad for a polyomino with birotary symmetry also uses 13-ominoes:
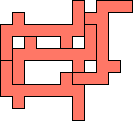
The smallest tetrads for polyominoes with birotary symmetry about an edge use 14-ominoes:
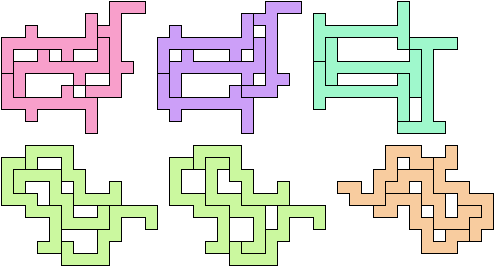
The smallest tetrads for polyominoes with mirror symmetry about an edge use 18-ominoes:
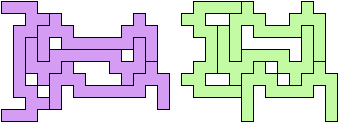
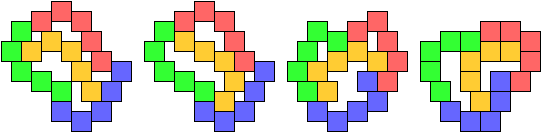
The smallest tetrads for polyominoes with birotary symmetry about a vertex also use 18-ominoes:

Juris Čerņenoks found the smallest tetrads for polyominoes with diagonal symmetry, which use 19-ominoes:
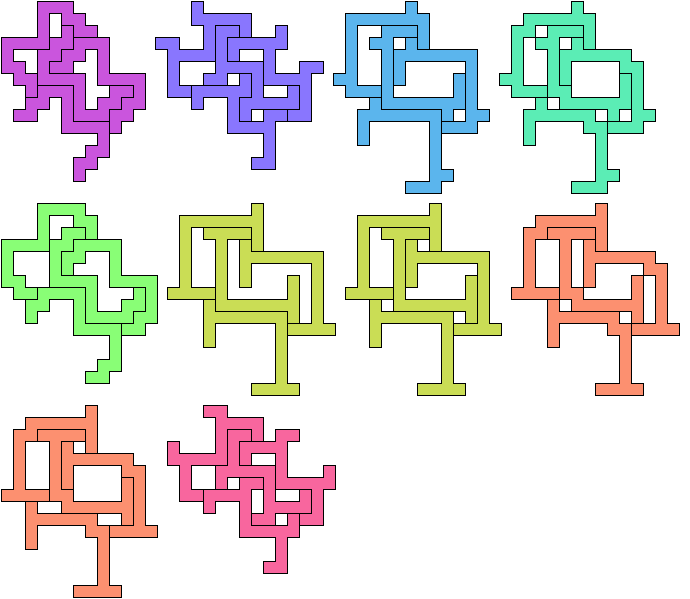

The smallest polyominoes that form tetrads without 90° rotation are 13-ominoes:
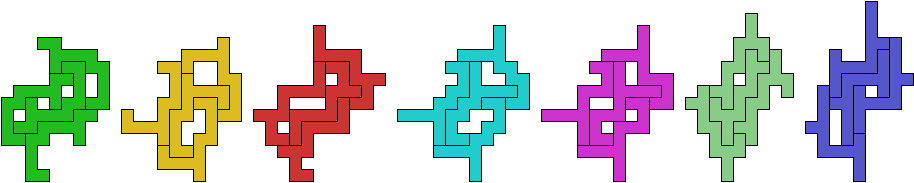
The smallest known holeless tetrad for a symmetric polyomino was found independently by Frank Rubin and Karl Scherer. It uses 34-ominoes:

Last revised 2020-01-14.